A planet revolves around the sun in elliptical orbit of eccentricity 'e'. If 'T' is the time period of the planet then the time spent by the planet between the end of the minor axis and close to the sun is
A
Tπ2e
B
T(2eπ−1)
C
Te2π
D
T(14−e2π)
Video Solution
Text Solution
The correct Answer is:D
(d) 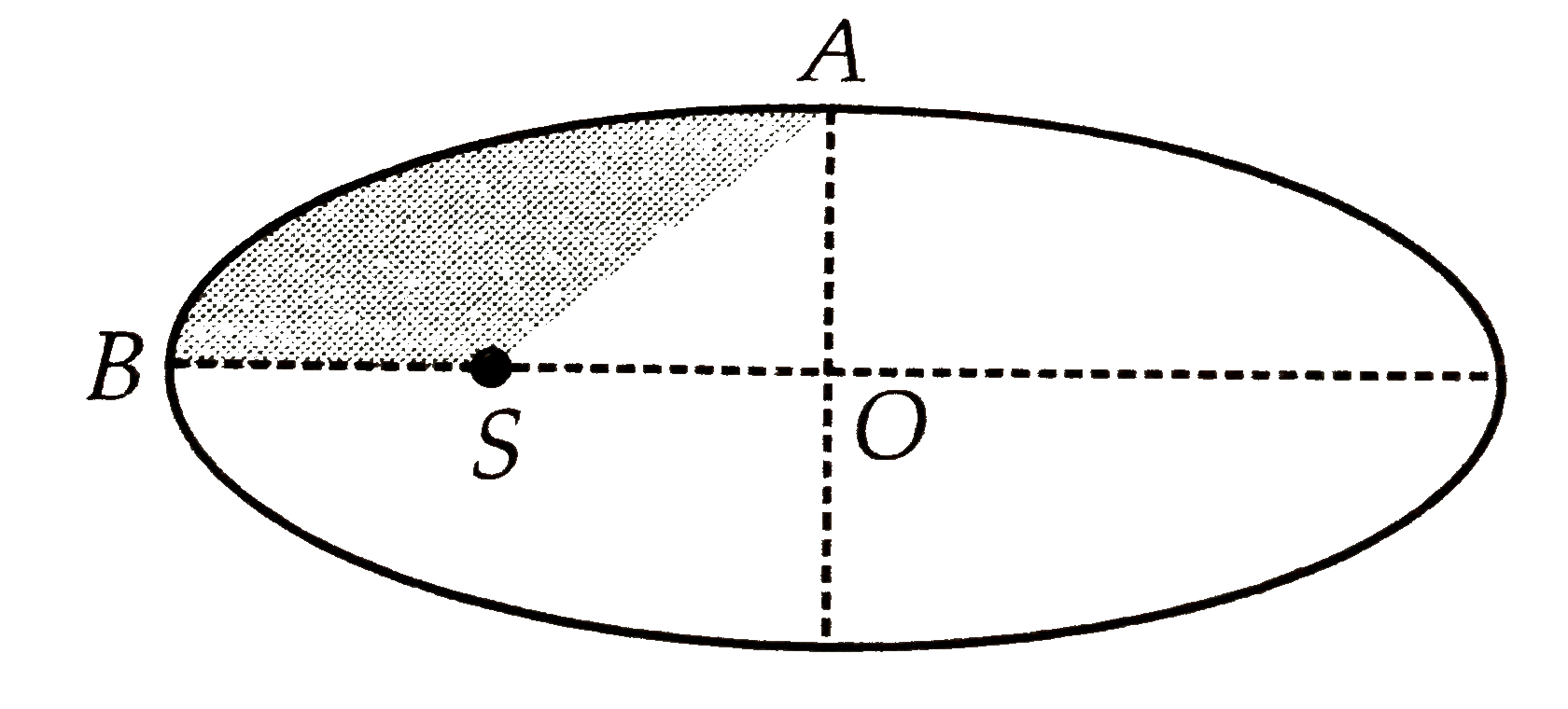
As a real velocity of a planet around the sun is constant. Therefore, the desired time is
tAB=(area ABS area of ellipse)× time period
If a= semi-major axis and b=semi- minor axis of ellipse, then , area of ellipse =πab
Area ABS=14(area of ellipse)- Area of triangle ASO
14×πab−12(ea)×(b)
∴tAB=[π(ab)4−12eab]πab×T−T(14−e2π)
|
Topper's Solved these Questions
- GRAVITATIONBOOK - NCERT FINGERTIPSCHAPTER - GRAVITATIONEXERCISE - Universal Law Of Gravitations
14 Videos
- GRAVITATIONBOOK - NCERT FINGERTIPSCHAPTER - GRAVITATIONEXERCISE - The Gravitational Constant
2 Videos
- KINETIC THEORYBOOK - NCERT FINGERTIPSCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason
10 Videos
Similar Questions
Knowledge Check
A planet is revolving round the sun in an elliptical orbit, If v is the velocity of the planet when its position vector from the sun is r, then areal velocity of the planet is
A|v×r|B2|r×v|C∣∣∣12(r×v)∣∣∣DNone of theseA planet is revolving around the sun as shown in elliptical path. The correct option is
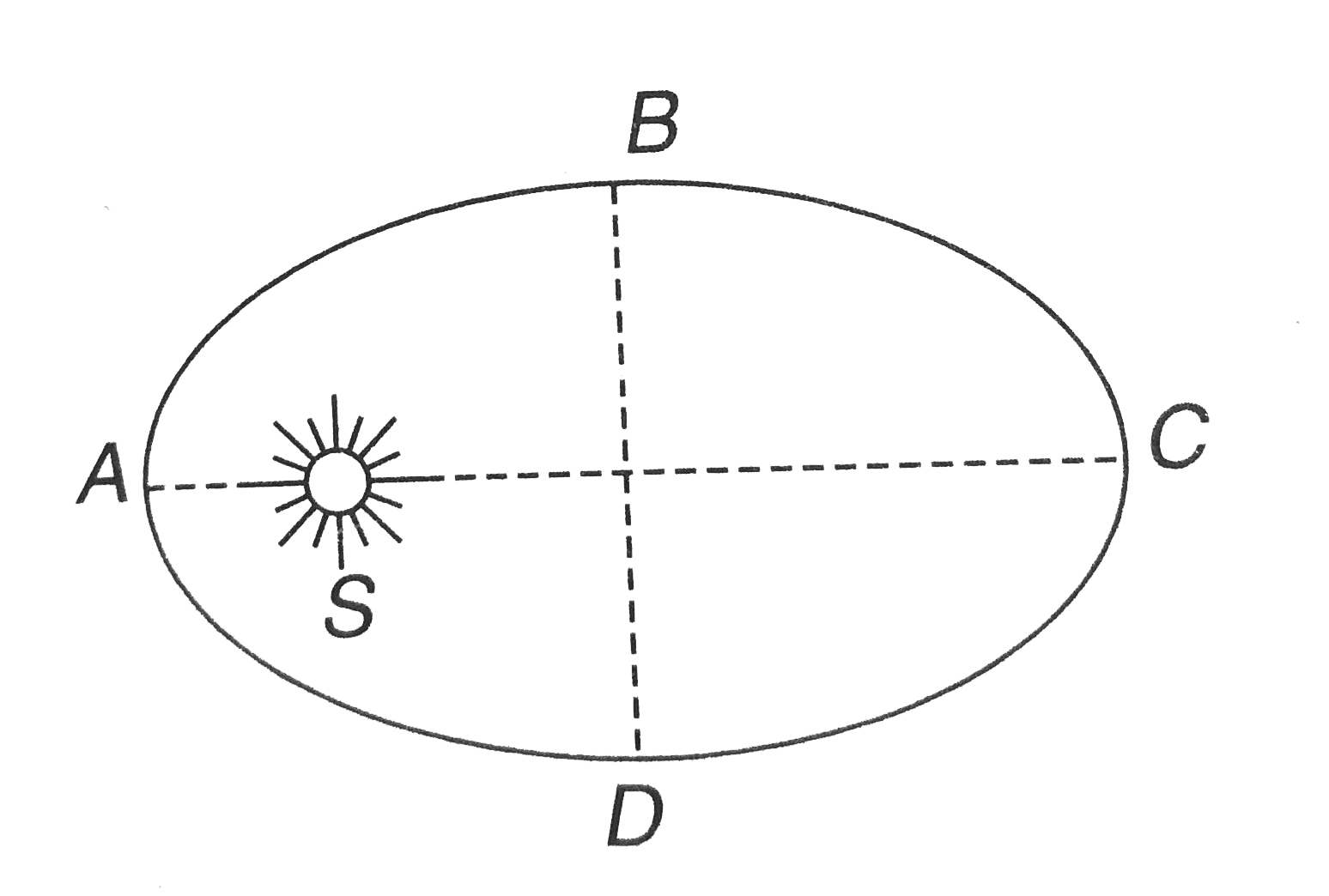 AThe time taken in travelling DAB is less than that for BCDBThe time taken in travelling DAB is greater than that for BCDCThe time taken in travelling CDA is less than that for ABCDThe time taken in travelling CDA is greater than that for ABC
AThe time taken in travelling DAB is less than that for BCDBThe time taken in travelling DAB is greater than that for BCDCThe time taken in travelling CDA is less than that for ABCDThe time taken in travelling CDA is greater than that for ABCA planet is revolving round the sun in an elliptical orbit. Of the following the property which is a constant during the motion of the planet is :
AThe force of attraction between the planet and sun.BThe total energy of the planet plus sun system.CThe linear momentum of the planet.DThe kinetic energy of the planet about the sun.
If a planet of mass m is revolving around the sun in a circular orbit of radius r with time period, T then mass of the sun is
View SolutionConsider a planet moving in an elliptical orbit around the Sun. The work done on the planet by the gravitational force of the Sun
View SolutionFor a planet revolving round the sun, when it is nearest to the sun
View SolutionA planet revolves around the sun in an elliptical orbit. If vp and va are the velocities of the planet at the perigee and apogee respectively, then the eccentricity of the elliptical orbit is given by :
View SolutionAsteroids revolve around the sun between the orbits of the planets :
View Solution