A plano-convex lens fits exactly into a plano-concave lens. Their plane surfaces are parallel to each other. If the lenses are made of different material of refractive indices μ1 and μ2 and R is the radius of curvature of the curved surface of the lenses, then focal length of the combination is
R2(μ1+μ2)
R2(μ1−μ2)
R(μ1−μ2)
2Rμ1=μ2
The correct Answer is:c
Focal length of combination
1f=1f1+1f2
Using lens maker’s formula
1f2=(μ2−1)(1−R−1∞)=−(μ2−1)R
1f1=(μ1−1)(1∞−1−R)=μ1−1R
or 1f1=(μ−1)R
1f2=−(μ2−1)R

Putting these values in Eq (i), we get
⇒1f=(μ1−1)R−(μ2−1)R
⇒1f=(μ1−1−μ2+1)R
⇒1f=μ1−μ2R
f=R(μ1−μ2)
Topper's Solved these Questions
Similar Questions
A plano convex lens fits exactly into a plano concave lens. Their plane surfaces are parallel to each other. If lenses are made of different materials of refractive index μ1=4/3 and μ2=6/5 and R = 40 cm is the radius of curvature of the curved surface of the lenses, then the focal length of combination (in meters) is.
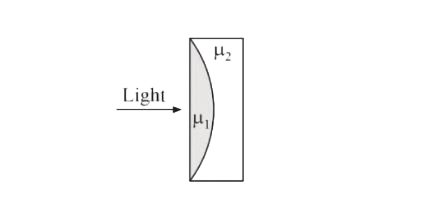
View SolutionFind the radius of curvature of convex surface of a plano convex lens, whose focal length is 0.3mandμ=1.5.
View Solution
Knowledge Check
A plano convex lens fits exactly into a plano concave lens. Their plane surfaces are parallel to each other. If the lenses are made of different materials refractive indices μ1 and μ2 and R is the radius curvature of the curved surface of the lenses, the focal length of the combination is
ARμ1−μ2B2Rμ2−μ1CR2(μ1−μ2)DR2−(μ1+μ2)A plano-convex lens fits exactly into a plano-concave lens. Their plane surfaces are parallel to each other. If the lenses are made of different material of refractive indices μ1 and μ2 and R is the radius of curvature of the curved surface of the lenses, then focal length of the combination is
ARμ1−μ2B2Rμ1−μ2CR2(μ1−μ2)DR2−(μ1+μ2)A plano-convex lens fits exactly into a plano-concave lens. Their plane surfaces are parallel to each other. If the lenses are made of different material of refractive indices μ1 and μ2 and R is the radius of curvature of the curved surface of the lenses, then focal length of the combination is
AR2(μ1+μ2)BR2(μ1−μ2)CR(μ1−μ2)D2Rμ1=μ2
A biconcave lens is made of a material of refractive index μ. If the radius of curvature of each face of the lens is 32 times the focal length of lens, calculate value of μ.
View SolutionA thin plano-convex lens fits exactly into a thin plano-concave lens. Their plane surfaces are parallel to each other. The lenses are made of different material of refractive indices μ1 and μ2 and R is the radius of curvature of the curved surfaces of the lenses, if rays are incident parallel to principal axis on lens of refractive index.
View SolutionA plano-convex lens is made of refractive index 1.6. The radius of curvature of the curved surface is 60 cm. The focal length of the lens is
View SolutionA plano-convex lens is made of glass of refractive index 1.6. the radius of curvature of its curved surface is 30 cm. What is the focal length of the lens ?
View SolutionA planocovex lens is made of a material of refractive in μ=1.5 The radius of curvature of curved surface of the lens is 20.cm. If its plane surface3 is silvered, the focal length of the silvered lens will be
View Solution
