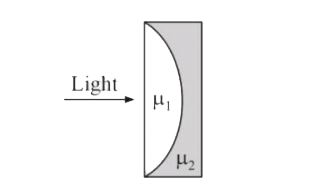
A plano convex lens fits exactly into a plano concave lens. Their plane surfaces are parallel to each other. If lenses are made of different materials of refractive index μ1=4/3 and μ2=6/5 and R = 40 cm is the radius of curvature of the curved surface of the lenses, then the focal length of combination (in meters) is.

The correct Answer is:3
The equivalent focal length (f) of the given lens as shown in figure is given by
1f=1f1+1f2
1f=(μ1−1)(1∞−1−R)+(μ2−1)(1−R−1∞)
=(μ1−1)R−(μ2−1)R=μ1−μ2R, f=Rμ1−μ2
Similar Questions
Find the radius of curvature of convex surface of a plano convex lens, whose focal length is 0.3mandμ=1.5.
View SolutionA thin plano-convax lens fits exactly into a plano concave lens with their plane surface parallel to each other as shown in the figure.the radius of the curvature of the curved surface R=30cm The lens ar made of different material having refractive indexμ1=32and μ2=54as shown in the figure

(i) if plane surface of hte plano -convex lens is silvered,then calculate the equivalent focal length of this system and also calculate the nature of the is equivalent mirror .
(ii) An object having transverse length 5cminplaced ont he axis of equivalenet mirror(in part1)atadistance15cm from the equivalent mirror alone principal axis.Find teh transverse magnification prodcuied by equivalents mirror.
View Solution
Knowledge Check
A plano-convex lens fits exactly into a plano-concave lens. Their plane surfaces are parallel to each other. If the lenses are made of different material of refractive indices μ1 and μ2 and R is the radius of curvature of the curved surface of the lenses, then focal length of the combination is
ARμ1−μ2B2Rμ2−μ1CR2(μ1−μ2)DR2−(μ1−μ2)A plano convex lens fits exactly into a plano concave lens. Their plane surfaces are parallel to each other. If the lenses are made of different materials refractive indices μ1 and μ2 and R is the radius curvature of the curved surface of the lenses, the focal length of the combination is
ARμ1−μ2B2Rμ2−μ1CR2(μ1−μ2)DR2−(μ1+μ2)A plano-convex lens fits exactly into a plano-concave lens. Their plane surfaces are parallel to each other. If the lenses are made of different material of refractive indices μ1 and μ2 and R is the radius of curvature of the curved surface of the lenses, then focal length of the combination is
AR2(μ1+μ2)BR2(μ1−μ2)CR(μ1−μ2)D2Rμ1=μ2
A plano-convex lens fits exactly into a plano-concave lens. Their plane surfaces are parallel to each other. If the lenses are made of different material of refractive indices μ1 and μ2 and R is the radius of curvature of the curved surface of the lenses, then focal length of the combination is
View SolutionA thin plano-convex lens fits exactly into a thin plano-concave lens. Their plane surfaces are parallel to each other. The lenses are made of different material of refractive indices μ1 and μ2 and R is the radius of curvature of the curved surfaces of the lenses, if rays are incident parallel to principal axis on lens of refractive index.
View SolutionThe radius of curvature of each surface of a lens is 40 cm. Its refractive index is 1.5. The focal length of lens will be
View SolutionA plano-convex lens is made of refractive index 1.6. The radius of curvature of the curved surface is 60 cm. The focal length of the lens is
View SolutionA planocovex lens is made of a material of refractive in μ=1.5 The radius of curvature of curved surface of the lens is 20.cm. If its plane surface3 is silvered, the focal length of the silvered lens will be
View Solution
