A point charge Q is placed at the origin . Find the electrostatic energy stored outside the sphere of radius R centred at the origin.
To find the electrostatic energy stored outside a sphere of radius R centered at the origin with a point charge Q placed at the origin, we can follow these steps:
Step 1: Understand the Concept of Electrostatic Energy
The electrostatic energy E stored in a capacitor or a system of charges can be calculated using the formula:
E=12Q2C
where C is the capacitance of the system.
Step 2: Determine the Capacitance of a Sphere
For a spherical surface of radius R, the capacitance C is given by:
C=4πϵ0R
where ϵ0 is the permittivity of free space.
Step 3: Substitute the Capacitance into the Energy Formula
Now, we can substitute the expression for capacitance into the energy formula:
E=12Q24πϵ0R
Step 4: Simplify the Expression
Now simplify the expression for E:
E=Q28πϵ0R
Final Result
Thus, the electrostatic energy stored outside the sphere of radius R centered at the origin is:
E=Q28πϵ0R
The electrostatic energy E stored in a capacitor or a system of charges can be calculated using the formula:
E=12Q2C
where C is the capacitance of the system.
For a spherical surface of radius R, the capacitance C is given by:
C=4πϵ0R
where ϵ0 is the permittivity of free space.
Now, we can substitute the expression for capacitance into the energy formula:
E=12Q24πϵ0R
Now simplify the expression for E:
E=Q28πϵ0R
Thus, the electrostatic energy stored outside the sphere of radius R centered at the origin is:
E=Q28πϵ0R
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - short answer7videos
CAPACITORS
- BOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE 26videos
CAPACITORS
- BOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Short Answer10videos
BOHR'S MODEL AND PHYSICS OF THE ATOM
- BOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer6videos
DISPERSION AND SPECTRA
Similar Questions
A metal sphere of radius R is charged to a pontital V . (a ) Find the electrostatic energy stored in the electric field within a concentric sphere of radius 2 R . (b )Show that the electrostatic field energy stored outside the sphere of radius 2R equals that stored within it .
View SolutionA point charge q is placed at the origin . How does the electric field due to the charge very with distance r from the origin ?
View SolutionA point charge Q is placed at the origin of the coordinate system. What is the electrostatic energy within an annular spherical region, with centre at origin and inner and outer radii R and 2R respectively.
View SolutionA point charge q is placed at origin. Find the flux of electric,produced due to this charge, through a circle of radius R lying in y-z plane. The centre of the circle lies at (x,0).
View SolutionA point charge +Q is placed at the centre of an isolated conducting shell of radius R. Find the electrostatic potential energy stored outside the spherical shell if the shell also contains charge +Q distributed uniformly over it.
 View Solution
View SolutionElectric field in a region of space is radially outward from origin and varies with distance 'r' from origin as E = kr. Find the charge enclosed in a sphere of radius 'a' centred at origin.
View SolutionInside a neutral hollow conducting sphere of radius X and centre C, a point charge q is placed as shown in the figure. Another point charge q1, is placed outside the sphere at distance d from centre. The net- electrostatic force on charge q placed at the centre is K=14πε0
 View Solution
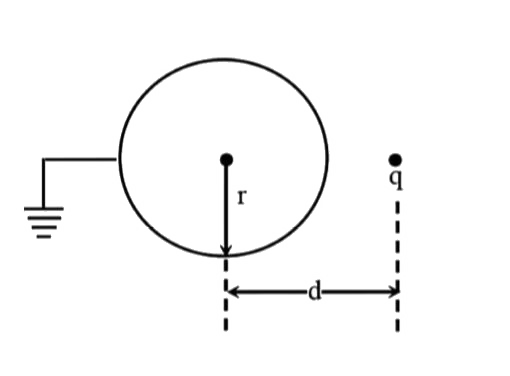
View SolutionA point charge q is placed at some distance d away from the centre of a grounded conducting sphere of radius r, as shown in the figure. The charge that flows the earth to the sphere is
 View Solution
View SolutionA conducting shell of radius R carries charge −Q. A point charge +Q is placed at the centre. The electric field E varies with distance r (from the centre of the shell) as
View SolutionA thin spherical conducting shell of radius R has a charge q. Another charge Q is placed at the centre of the shell. The electrostatic potential at a point P a distance R2 from the centre of the shell is
View Solution
