Figure shows two indentical pallel plate capacitors connected to a switch S. Initially ,the switch is closed so that the capacitors are completely charged .The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constant 3. Find the ratio of the initial total energy stored in the capacitors to the final total energy stored.
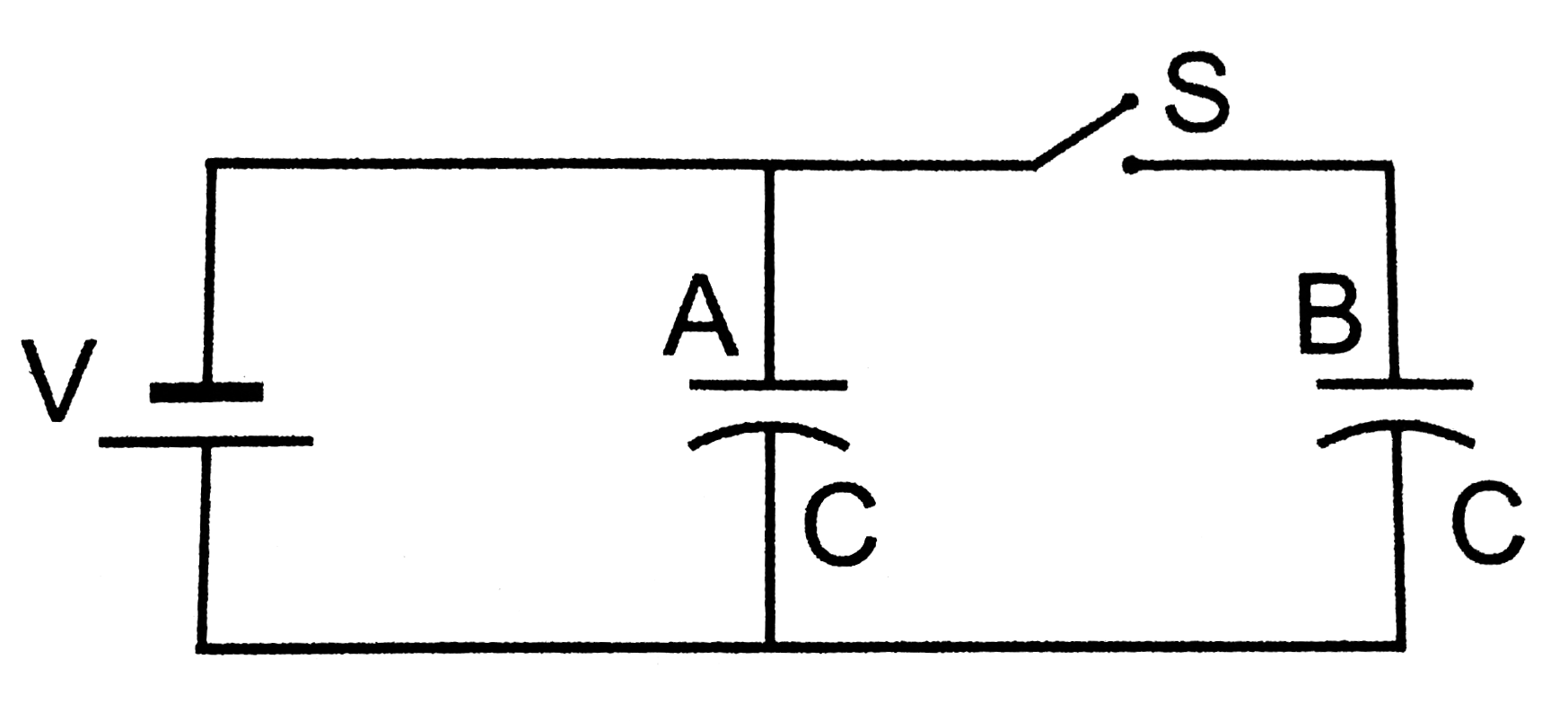
Initial total energy
=12CV2+12CV2=CV2
when the switch is open dielectric induced. Then capacitance
C=123CV2=32CV2
Since switch is open so change be same in B so Energy in
B=12.C3.V2
So, total final energy
=32CV2+16CV2
=9CV2+1CV26=106CV2
So, required ratio =CV2106CV2=35=3.5 .
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - short answer7videos
CAPACITORS
- BOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE 26videos
CAPACITORS
- BOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Short Answer10videos
BOHR'S MODEL AND PHYSICS OF THE ATOM
- BOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer6videos
DISPERSION AND SPECTRA
Similar Questions
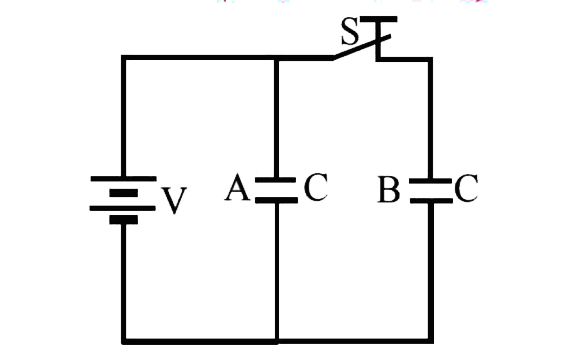
The figure shows two identical parallel plate capacitors connected to a battery with the switch S closed. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constant(or relative permittivity) 3. Find the ratio of the total electrostatic energy stored in both capacitors before and after the introduction of the dielectric.
 View Solution
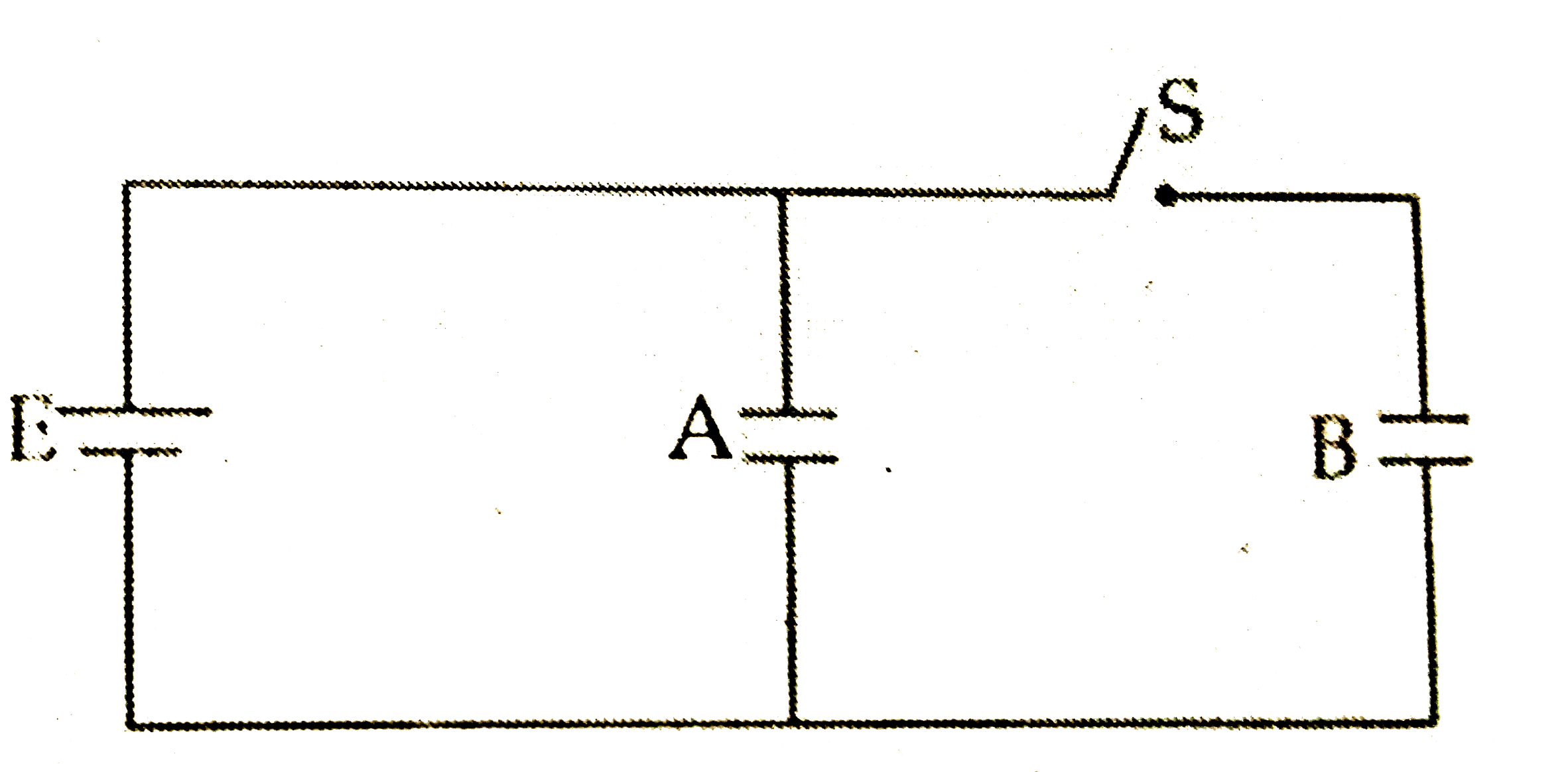
View SolutionTwo identical parallel plate capacitors A and B are
connected to a battery of V volts with the switch S
closed . The switch is now opend and the free
space between the plantes of the capacitors is filled
with a dielectric of dielectric constant K. Find the
rario of the total electrostatic energy stored in both
capacitors before and after the introduction of the dielectric.
 View Solution
View SolutionHalf of the space between the plates of a parallel plate capacitor is filled with dielectric material of constant K. Then which of the plots are possible?
View SolutionThe terminals of a battery of emf V are connected to the two plates of a parallel plate capacitor. If the space between the plates of the capacitor is filled with an insulator of dielectric constant K, then :
View SolutionTwo parallel plate capacitors, each of capacitance 40 muF, are connected is series. The space between the plates of one capacitor is filled with a dielectric material of dielectric constant K =4. Find the equivalent capacitacne of the system.
View SolutionA parallel plate capacitar, of capacitance, 20μF, is connected to a 100 V supply. After some time, the battery is disconnected , and the space, between the plates of the capacitor is filled with a dielectric, of dielectric constant 5. Calculate the energy stored in the capacitar (i) before (ii)after dielectric has been put in between its plates.
View SolutionConsider a disconnected plate capacitor of capacity 10μF with air filled in the gap between the plates. Now one-half of the space between the plates is filled with a dielectric of dielectric constant 4 as shown in .The capacity of the capacitor changes to
 .View Solution
.View SolutionConsider a parallel plate capacitor of 10μF (micro-farad) with air filled in the gap between the plates. Now one half of the space between the plates is filled with a dielectric of dielectric constant 4, as shown in the figure. The capacity of the capacitor charges to
 View Solution
View SolutionThe capacitance of a parallel plate capacitor is C when the region between the plate has air. This region is now filled with a dielectric slab of dielectric constant k. The capacitor is connected to a cell of emfE, and the slab is taken out
View SolutionTwo parallel plate capacitors of capacitances C and 2C are connected in parallel and charged to a potential difference V. The battery is then disconnected and the region between the plates of the capacitor C is completely filled with a material of dielectric constant K. The potential differences across the capacitors now becomes...........
View Solution

