A point charge Q is situated (outside) at a distance r from the centre of an uncharged conducting solid sphere of radius R. The potential due to induced charges (on the conductor) at a point B inside the conductor whose distance form the point charge is d is ______
To solve the problem, we need to determine the potential at point B inside a conducting solid sphere due to the induced charges when a point charge Q is placed outside the sphere. Here’s a step-by-step solution:
Step 1: Understand the setup
We have a point charge Q located outside a conducting solid sphere with radius R. The distance from the center of the sphere to the point charge is r. We also have a point B inside the conductor, which is at a distance d from the point charge Q.
Step 2: Recognize the properties of conductors
In electrostatics, the electric field inside a conductor in electrostatic equilibrium is zero. Therefore, the potential inside the conductor is constant and equal to the potential on its surface.
Step 3: Calculate the potential at point B
The total potential VB at point B due to the point charge Q and the induced charges can be expressed as:
VB=VQ+Vinduced
Where:
- VQ is the potential due to the point charge Q.
- Vinduced is the potential due to the induced charges on the conducting sphere.
Step 4: Calculate the potential due to the point charge
The potential VQ at point B due to the point charge Q is given by:
VQ=kQd
where k is Coulomb's constant.
Step 5: Calculate the potential due to induced charges
The potential due to the induced charges on the conducting sphere at point B is equal to the potential on the surface of the sphere, which can be calculated as:
Vinduced=kQR
This is because the induced charges redistribute themselves such that the potential inside the conductor is constant and equal to the potential on the surface.
Step 6: Combine the potentials
Now, substituting the values we calculated:
VB=kQd+kQR
Step 7: Final expression for the potential due to induced charges
To find the potential due to the induced charges alone, we rearrange the equation:
Vinduced=VB−VQ=kQR−kQd
Thus, the potential due to induced charges at point B inside the conductor is:
Vinduced=kQ(1R−1d)
Final Answer
The potential due to induced charges at point B inside the conductor is:
Vinduced=kQ(1R−1d)
We have a point charge Q located outside a conducting solid sphere with radius R. The distance from the center of the sphere to the point charge is r. We also have a point B inside the conductor, which is at a distance d from the point charge Q.
In electrostatics, the electric field inside a conductor in electrostatic equilibrium is zero. Therefore, the potential inside the conductor is constant and equal to the potential on its surface.
The total potential VB at point B due to the point charge Q and the induced charges can be expressed as:
VB=VQ+Vinduced
Where:
- VQ is the potential due to the point charge Q.
- Vinduced is the potential due to the induced charges on the conducting sphere.
The potential VQ at point B due to the point charge Q is given by:
VQ=kQd
where k is Coulomb's constant.
The potential due to the induced charges on the conducting sphere at point B is equal to the potential on the surface of the sphere, which can be calculated as:
Vinduced=kQR
This is because the induced charges redistribute themselves such that the potential inside the conductor is constant and equal to the potential on the surface.
Now, substituting the values we calculated:
VB=kQd+kQR
To find the potential due to the induced charges alone, we rearrange the equation:
Vinduced=VB−VQ=kQR−kQd
Vinduced=kQ(1R−1d)
The potential due to induced charges at point B inside the conductor is:
Vinduced=kQ(1R−1d)
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.4
15 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
A point charge q is placed at a distance of r from cebtre of an uncharged conducting sphere of rad R(<r). The potential at any point on the sphere is
View SolutionA point charge q , is placed at a distance r from the centre of an aluminium sphere, of radius R (r>R) . Selectr the correct alternatives.
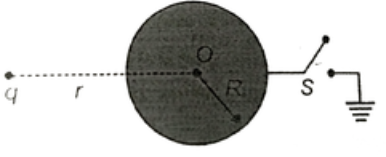
View SolutionA charge q is placed at a distance of 2R from the centre of a spherical conducting shell of radius R. What is electrical potential, due to charges induced on the shell, at a point which is farthest from the point charge ?
View SolutionPotential at a point x-distance from the centre inside the conducting sphere of radius R and charged with charge Q is
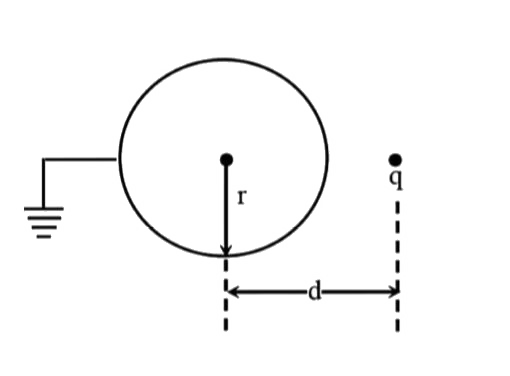
View SolutionA point charge q is placed at some distance d away from the centre of a grounded conducting sphere of radius r, as shown in the figure. The charge that flows the earth to the sphere is
View SolutionA point charge q is placed at a distance of r from the centre O of an uncharged spherical shell of inner radius R and outer radius 2R. The electric potential at the centre of the shell will be

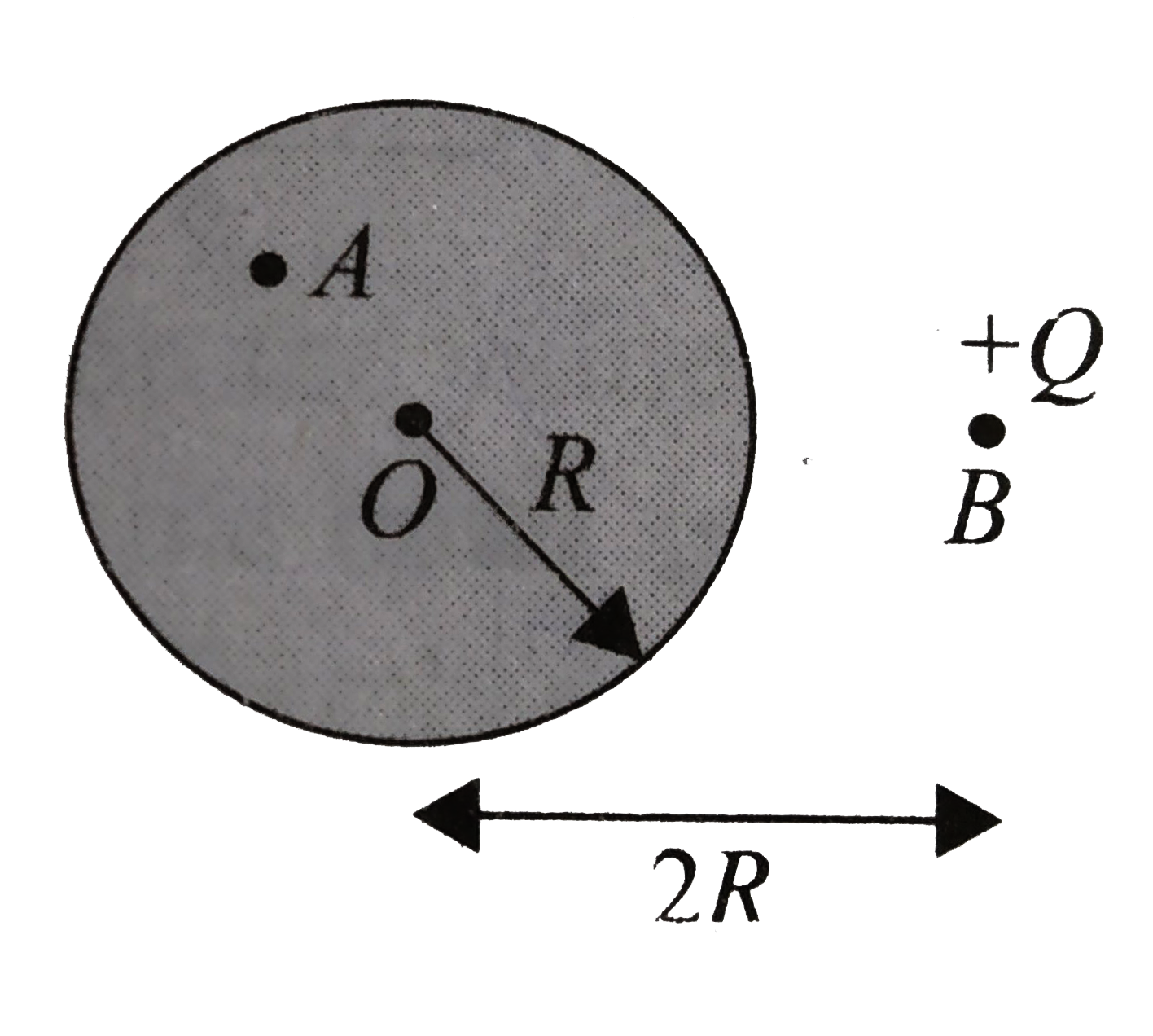
View SolutionA point charge +Q is placed at point B at a distance 2R from the center O of an uncharged thin conducting shell of radius R as shown in figure. If VA be the potential at point A, which is at a radial distance of R/2 from the center of the shell, then
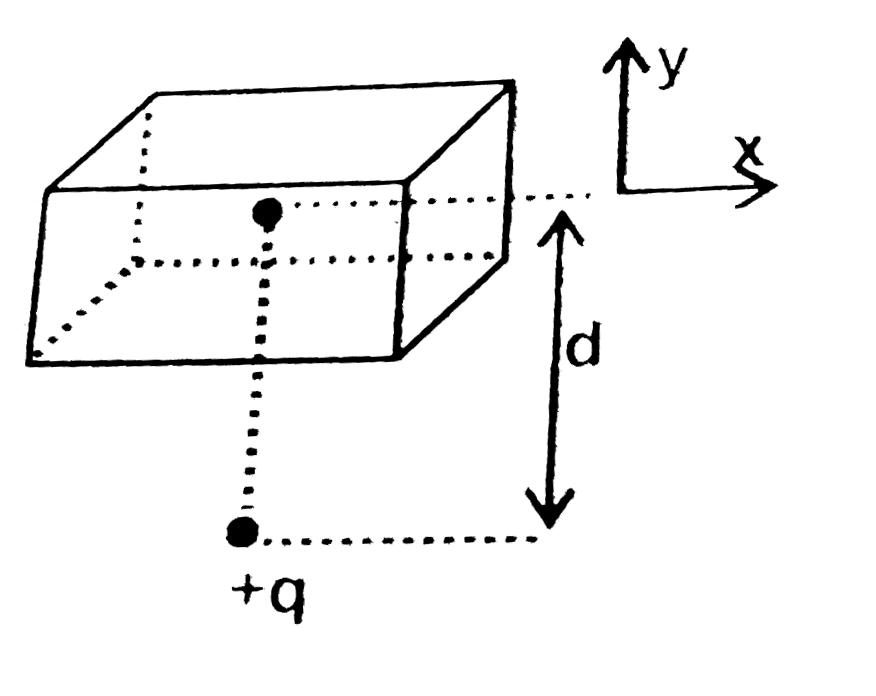
View SolutionA charge +q is placed at a distance 'd' from the centre of the uncharged metallic cube of side 'a'. The electric field at the centre of the cube due to induced charges on the cube will be
View SolutionA point charge q is placed at a distance d from the centre of a circular disc of radius R. Find electric flux flowing through the disc due to that charge
View SolutionA positive point charge q is placed at a distance 2 R from the surface of a metallic shell of radius R. the electric field at centre of shell due to indouced charge has magnitude

View Solution
