Potential at a point x-distance from the centre inside the conducting sphere of radius and charged with charge is
zero
The correct Answer is:A
To find the potential at a point located at a distance x from the center inside a conducting sphere of radius R and charged with charge Q, we can follow these steps:
1. Understanding the Conducting Sphere:
- A conducting sphere with charge Q distributes its charge uniformly on its surface. Inside the conducting material, the electric field (E) is zero due to electrostatic shielding.
2. Applying Gauss's Law:
- According to Gauss's law, the electric field inside a conductor in electrostatic equilibrium is zero. Therefore, for any point inside the conducting sphere (at a distance x<R), we have:
E=0
3. Relating Electric Field to Potential:
- The electric potential V is related to the electric field by the equation:
V=−∫Edr
- Since the electric field E is zero inside the conducting sphere, the potential V remains constant throughout the interior of the sphere.
4. Determining the Potential:
- The potential inside the sphere is equal to the potential on the surface of the sphere. The potential V at the surface of a charged sphere is given by:
V=14πϵ0QR
- Therefore, the potential at any point inside the conducting sphere (including at a distance x from the center) is also:
V=14πϵ0QR
Final Answer:
Thus, the potential at a point x distance from the center inside the conducting sphere is:
V=14πϵ0QR
---
- A conducting sphere with charge Q distributes its charge uniformly on its surface. Inside the conducting material, the electric field (E) is zero due to electrostatic shielding.
- According to Gauss's law, the electric field inside a conductor in electrostatic equilibrium is zero. Therefore, for any point inside the conducting sphere (at a distance x<R), we have:
E=0
- The electric potential V is related to the electric field by the equation:
V=−∫Edr
- Since the electric field E is zero inside the conducting sphere, the potential V remains constant throughout the interior of the sphere.
- The potential inside the sphere is equal to the potential on the surface of the sphere. The potential V at the surface of a charged sphere is given by:
V=14πϵ0QR
- Therefore, the potential at any point inside the conducting sphere (including at a distance x from the center) is also:
V=14πϵ0QR
Thus, the potential at a point x distance from the center inside the conducting sphere is:
V=14πϵ0QR
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBook:DC PANDEY ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITORSExercise:(B) Chapter exercises
Explore 17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBook:DC PANDEY ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITORSExercise:(C) Chapter exercises
Explore 50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBook:DC PANDEY ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITORSExercise:Check point 2.5
Explore 20 Videos
- ELECTROMAGNETIC WAVESBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:Sec C
Explore 22 Videos
- ELECTROSTATICSBook:DC PANDEY ENGLISHChapter:ELECTROSTATICSExercise:Medical entrances gallery
Explore 37 Videos
Similar Questions
A conducting sphere of radius r has a charge . Then .
View SolutionSelf energy of conducting sphere of radius .r. carrying charge .Q. is ______
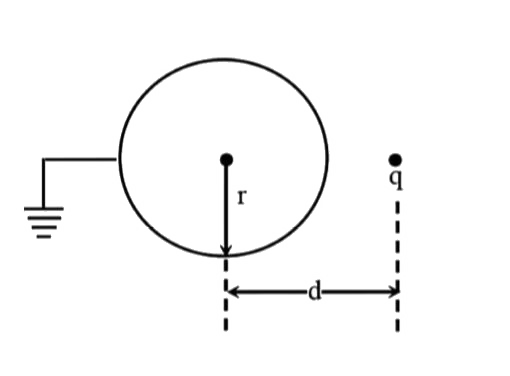
View SolutionA point charge q is placed at some distance d away from the centre of a grounded conducting sphere of radius r, as shown in the figure. The charge that flows the earth to the sphere is
View SolutionA point charge Q is situated (outside) at a distance r from the centre of an uncharged conducting solid sphere of radius R. The potential due to induced charges (on the conductor) at a point B inside the conductor whose distance form the point charge is d is ______
View SolutionThe electric field at a distance 3R/2 from the centre of a charge conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
View SolutionThe electric field at a distance 3R/2 from the centre of a charge conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
View SolutionA charge q is placed at a distance of 2R from the centre of a spherical conducting shell of radius R. What is electrical potential, due to charges induced on the shell, at a point which is farthest from the point charge ?
View Solution
A point charge q'q is placed at distance 'a' from the centre of an uncharged thin spherical conducting shell of radius R=2a. A point 'P' is located at a distance 4a from the centre of the conducting shell as shown. The electric potential due to induced charge on the inner surface of the conducting shell at point 'P' is
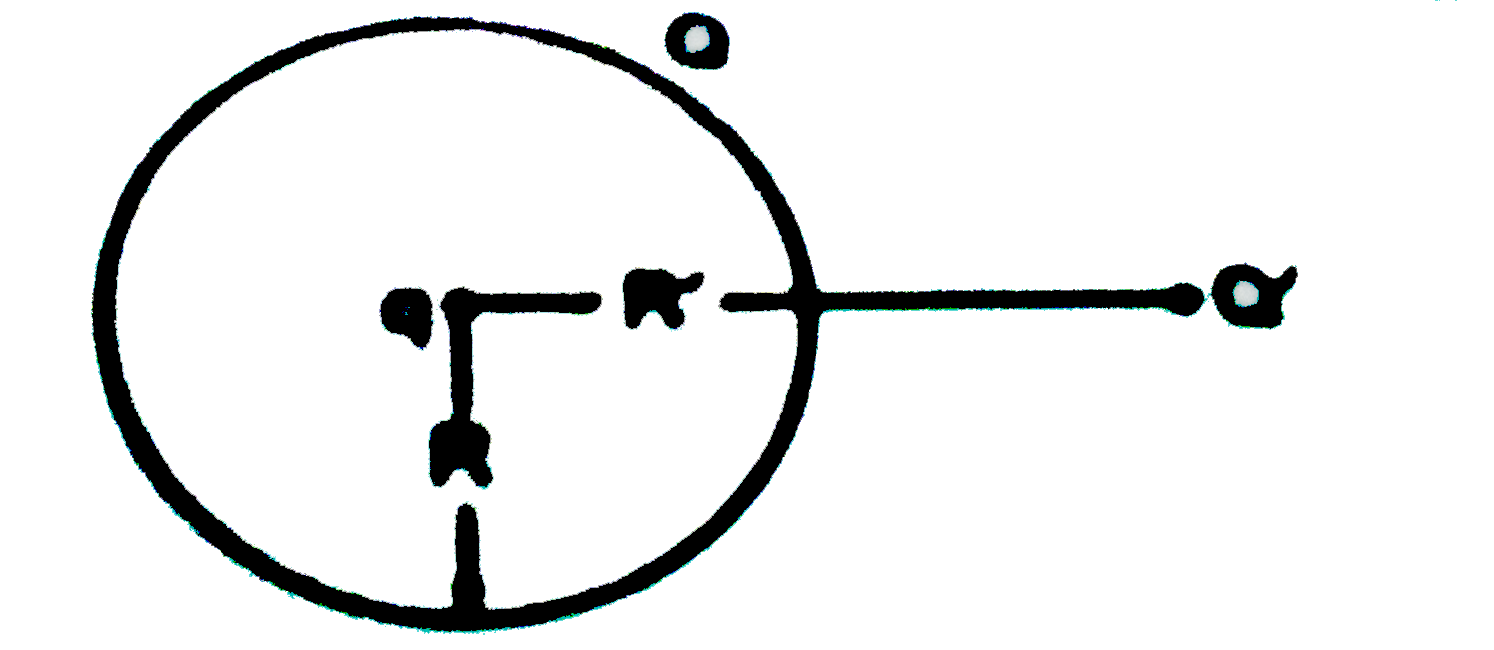
View SolutionA charge 'q' is placed at the centre of a conducting spherical shell of radius R, which is given a charge Q. An external charge Q' is also present at distance R'(R'>R) from 'q'. Then the resultant field will be best represented for region r<R by : [where r is the distance of the point from q]
View SolutionA solid non conducting sphere of radius R has a non-uniform charge distribution of volume charge density, ρ=ρ0rR, where ρ0 is a constant and r is the distance from the centre of the sphere. Show that : (i) the total charge on the sphere is Q=πρ0R3 (ii) the electric field inside the sphere has a magnitude given by, E=KQr2R4
View Solution