A point mass m connected to one end of inextensible string of length l and other end of string is fixed at peg. String is free to rotate in vertical plane. Find the minimum velocity given to the mass in horizontal direction so that it hits the peg in its subsequent motion.
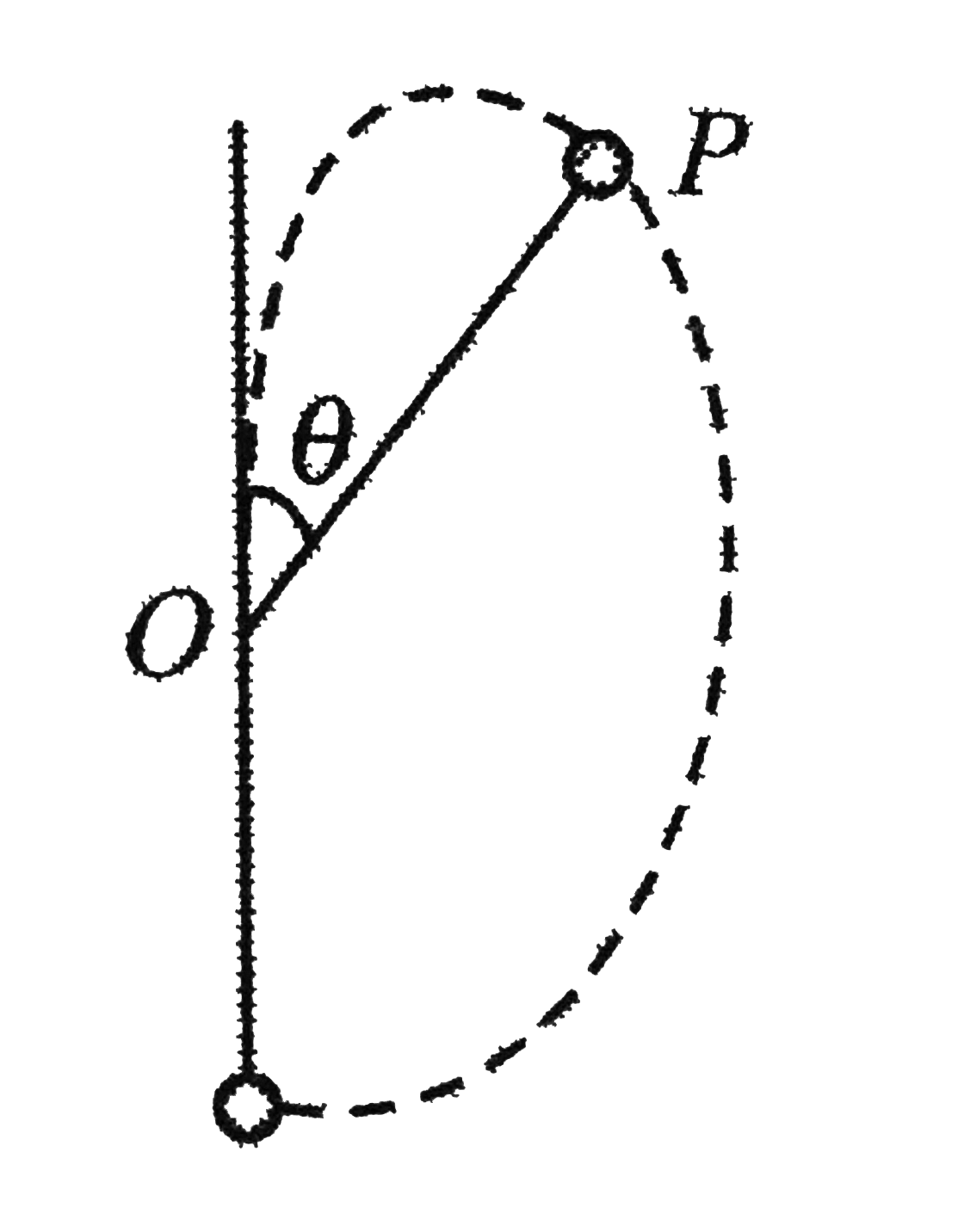
Tension in string is zero at point P in its subsequent motion, after this point its motion is projectile. Velocity at point P, T=0.
⇒mgcosθ=mv2lv=√glcosθ
Assume its projectile motion start at point P and it passes through point C. So that equation of trajectory satisfy the co-ordinate of C(lsinθ,−lcosθ)

Equation of trajectory,
y=xtanθ−gx22v2cos2θ
=(lsinθ)tanθ−g(lsinθ)22(glcosθ)cos2θ
=−cosθ=sin2θcosθ−12sin2θ2cos3θ
⇒−2cos4θ=2sin2θcos2θ−sin2θ
⇒sin2θ=2sin2θcos2θ+2cos4θ
=2cos2θ(sin2θ+cos2θ)
⇒tan2θ=2
⇒tanθ=√2 hence, cosθ=1√3, sinθ=√23
From energy conservation between point P and A,
12mu2=12mv2+mg(1+cosθ)
⇒u2=v2+2gl(1+cosθ)
=2gl+3glcosθ=2gl+3gl1√3
⇒u=[(2+√3)gl]1/2
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Solved Examples
15 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.1
25 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
Two point masses m are connected the light rod of length l and it is free to rotate in vertical plane as shown in figure. Calculate the minimum horizontal velocity is given to mass so that it completes the circular motion in vertical lane.
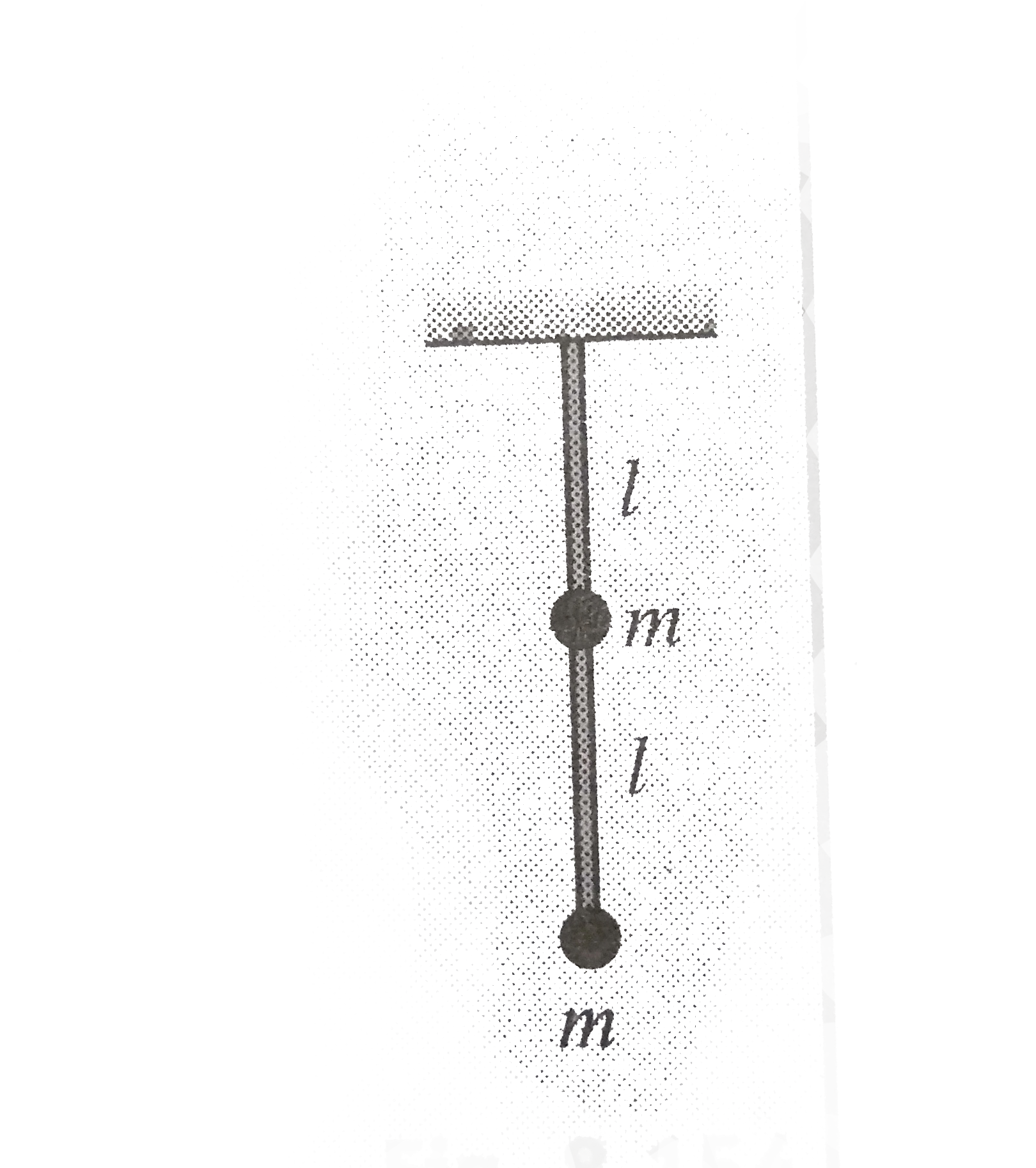
View SolutionA bob of mass m is suspended by a light inextensible string of length l from a fixed point such that it is free to rotate in a vertical plane. The bob is given' a speed of √4gl horizontally. The, height of the bob from the lower most point where the string just becomes slacked is nl3. Find n.
View Solution
Knowledge Check
A point mass m is connected with ideal inextensible string of length l and other end of string is tied at point O as shown in the figure. The string is made horizontal and mass is released from point A to perform vertical circular motion. There is a nail at point N such that ON =r . Find the value of r so that mass m is able to just perform complete vertical circular motion about point N.
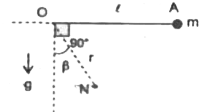 Al2+2cosβB3l3+2cosβCl3+2sinβD3l2+2sinβ
Al2+2cosβB3l3+2cosβCl3+2sinβD3l2+2sinβA mass m connected to inextensible string of length l lie on a horizontal smooth ground. Other end of string is fixed. Mass m is imparted a velocity v such that string remains taut & motion occurs in horizontal providely stirng during the time string turns through 90∘
 A2mvBmvC√2mvDm√2v2−2gl
A2mvBmvC√2mvDm√2v2−2glA particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl
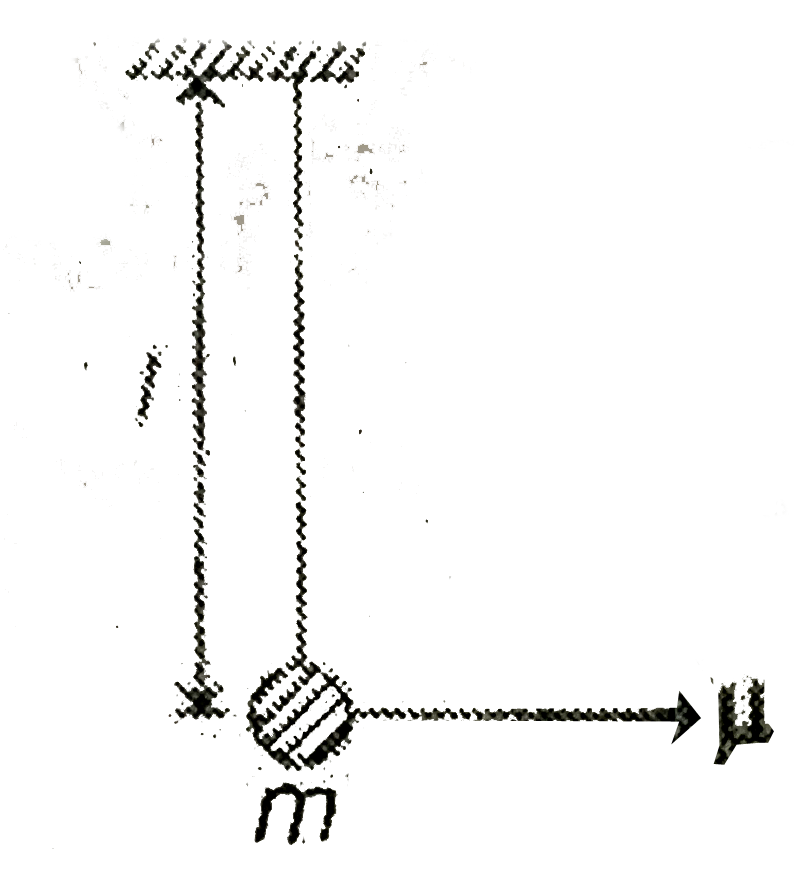
The tension in the string at an instant when acceleration of the particle is horizontal and √3g isAmgB2 mgC4 mgD6 mg
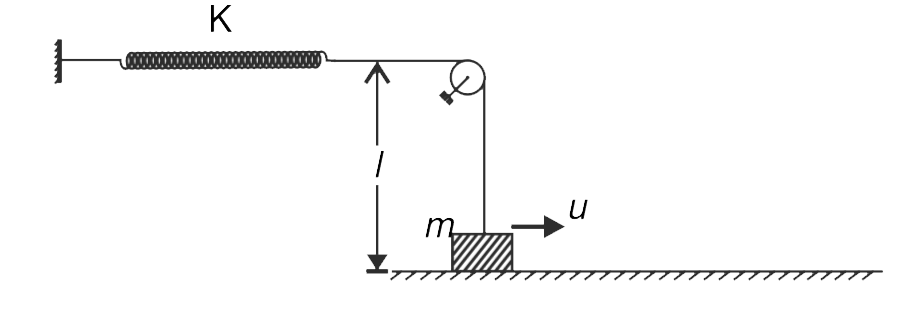
A ideal spring of force constant k is connected to a small block of mass m using an inextensible light string (see fig). The pulley is mass less and friction coefficient between the block and the horizontal surface is μ=1√3. The string between the pulley and the block is vertical and has length l. Find the minimum velocity u that must be given to the block in horizontal direction shown, so that subsequently it leaves contact with the horizontal surface. [Take k=2mgl]
View SolutionA pillar having square cross section of side length L is fixed on a smooth floor. A particle of mass m is connected to a corner A of the pillar using an inextensible string of length 3.5 L. With the string just taut along the line BA, the particle is given a velocity v perpendicular to the string. The particle slides on the smooth floor and the string wraps around the pillar.
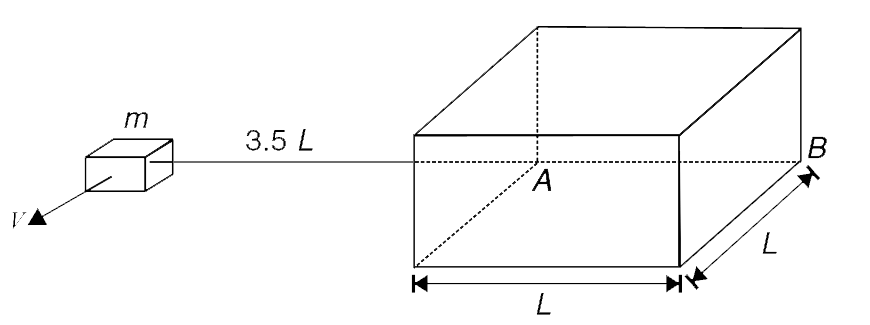
(a) Find the time in which the particle will hit the pillar. (b) Find the tension in the string just before the particle hits the pillar. Neglect any energy loss of the particle.
View SolutionA mass m is tied to a string of length l and is rotated in a vertical circle with centre at the other end of the string.
(a) Find the minimum velocity of the mass at the top of the circle so that it is able to complete the circle.
(b) Find the minimum velocity at the bottom of the circle corresponding to the above condition.
View SolutionA particle of maas m is attched to a light string of length l, the other end of which is fixed. Initially the string is kept horizontal and the particle is given an upwrd velocity v. The particle is just able to complete a circle
View SolutionA particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl
The maximum angle made by the string with downward vertical is
View Solution