Two point masses m are connected the light rod of length l and it is free to rotate in vertical plane as shown in figure. Calculate the minimum horizontal velocity is given to mass so that it completes the circular motion in vertical lane.
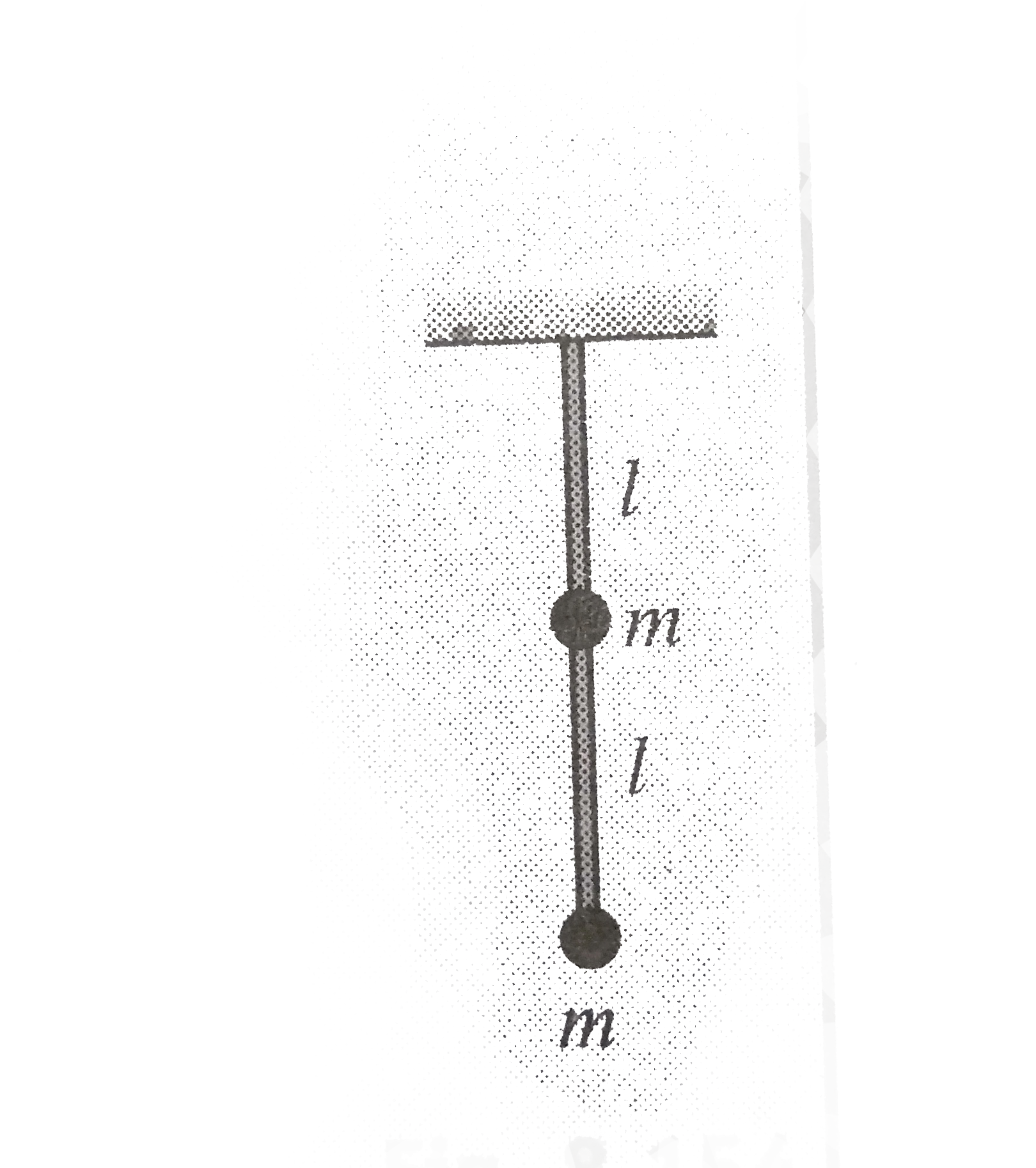
Here tenstion in the rod at the top most point of circle can be zero or negative for completing the loop. So velocity at the top most point is zero.
From energy conservation,
12mv2+12mv24=mg(2l)+mg(4l)+0
v=√48gl5
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.5
15 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Subjective
23 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.3
26 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A L shaped rod of mass M is free to rotate in a vertical plane about axis A A as shown in figure. Maximum angular acceleration of rod is

View SolutionA L shaped rod of mass M is free to rotate in a vertical plane about axis A A as shown in figure. Maximum angular acceleration of rod is

View Solution
Knowledge Check
A unifrom rod of length l and mass m is free to rotate in a vertical plane about A as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is
 A3g2lB3glCg2lD2gl
A3g2lB3glCg2lD2glA simple pendulum of effective length 'l' is kept in equilibrium in vertical position . What horizontal velocity should be given to its bob , so that it just completes a vertical circular motion ?
A√5glB√3glC√glD√7glA point mass m is connected with ideal inextensible string of length l and other end of string is tied at point O as shown in the figure. The string is made horizontal and mass is released from point A to perform vertical circular motion. There is a nail at point N such that ON =r . Find the value of r so that mass m is able to just perform complete vertical circular motion about point N.
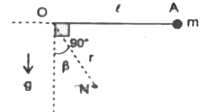 Al2+2cosβB3l3+2cosβCl3+2sinβD3l2+2sinβ
Al2+2cosβB3l3+2cosβCl3+2sinβD3l2+2sinβ
A uniform rod of length l and mass m is free to rotate in a vertical plane about A as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is

View SolutionA mass m is connected to a massless rod of length l( and is free to rotate in vertical plane about hinged end of rod. If rod is released from horizontal position and mass "m" collides inelastically at lowest position with identical mass m, as shown in the figure, then the maximum height attained by combined mass will be
View SolutionTwo particles of masses m and 2m are attached to the massless rod of length 2l as shown in figure. The rod is hinged at its midpoint O and is free to rotate in vertical plane about hinge. The minimum speed v at the given instant so that it can complete the circle.
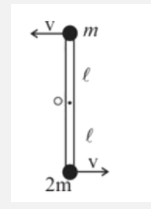
View SolutionTwo particles of masses m and 2m are attached to the massless rod of length 2l as shown in figure. The rod is hinged at its midpoint O and is free to rotate in vertical plane about hinge. The minimum speed v at the given instant so that it can complete the circle.

View SolutionA point mass m is connected with ideal inextensible string of length l and other end of string is tied at point O as shown in the figure. The string is made horizontal and mass is released from point A to perform vertical circular motion. There is a nail at point N such that ON =r . Find the value of r so that mass m is able to just perform complete vertical circular motion about point N.

View Solution
