A point mass m is suspended at the end of a massless wire of length l and cross section. If Y is the Young's modulus for the wire, obtain the frequency of oscillation for the simple harmonic motion along the vertical line.

Video Solution

Text Solution

Verified by Experts

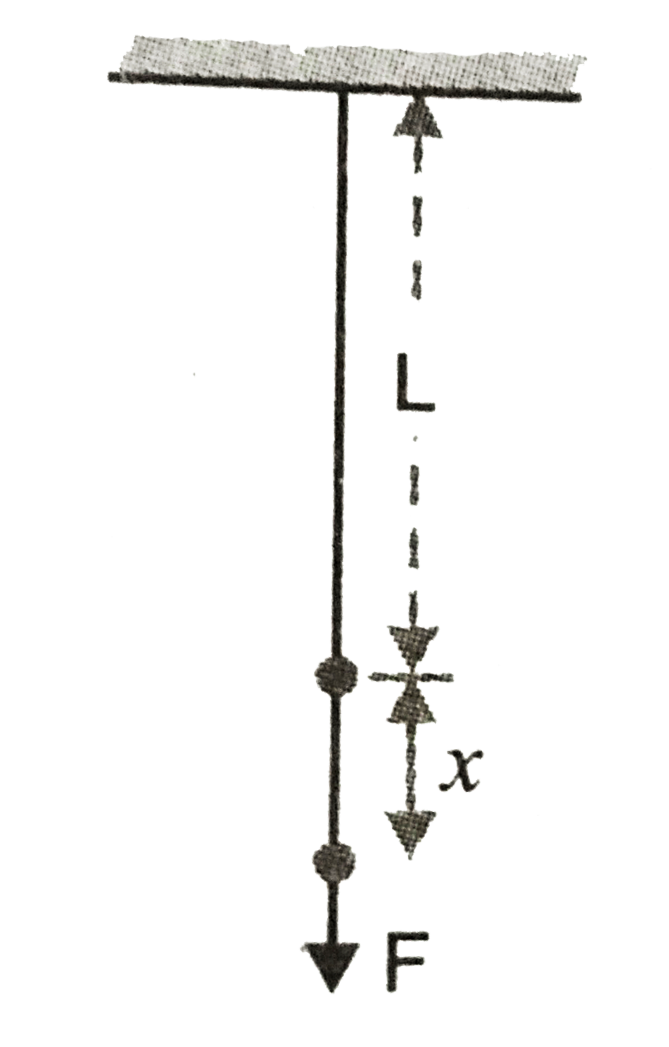
Let F be the force applied on the end of wire and x be the extension in the length of wire, figure,
longitudinal strain $= \frac{x}{L}$
Normal stress $= \frac{F}{A}$
Young's modulus $Y = \frac{F / A}{x / L} or F = Y A \frac{x}{L}$
The restoring force due to elasticity is
$F = - \frac{Y A}{L} x$ ...(i)
Since $F \propto x$ and this force F will tend to bring the body si left free, it will execute linear simple harmonic motion. Comparing (i) with the equation $F = - k y$
We have , spring factor , $k = \frac{Y A}{L}$
and inertia factor $=$ mass of body $=$ m .
As, frequency, $v = \frac{1}{2 π} \sqrt{\frac{s p r i n g f a c t o r}{i n e r t i a f a c t o r}}$
so $v = \frac{1}{2 π} \sqrt{\frac{Y A}{L m}}$

Updated on:21/07/2023

A point of mass m is suspended at the end of a massless wire of length l and cross-section A. If Y is the Young's modulus for the wire, obtain the frequency of oscillation for the simple harmonic motion along the vertical line.
[Hint: If x is the displacement of mass m from the equilibrium position then $Y = \frac{s t r e s s}{s t r a \in} = \frac{\frac{F}{A}}{\frac{x}{l}}$ or F = (YAx)/(l) and this force acts opposite to x. Now proceed as in example 3.
A $\frac{1}{2 π} \sqrt{\frac{Y A}{m L}}$
B $2 π \sqrt{\frac{m L}{Y A}}$
C $\frac{1}{π} \sqrt{\frac{Y A}{m L}}$
D $π \sqrt{\frac{m L}{Y A}}$
A mass (m) is suspended at the end of a weightless wire of length L, cross-sectional area A and Young's modulus Y. The period of oscillation for the S.H.M. along the vertical direction is,
A $2 π \sqrt{\frac{Y A}{m L}}$
B $2 π \sqrt{\frac{m L}{Y A}}$
C $2 π \sqrt{\frac{m Y}{A L}}$
D $2 π \sqrt{\frac{A L}{m Y}}$
A mass (m) is suspended at the end of a weightless wire of length L, cross-sectional area A and Young's modulus Y. The period of oscillation for the S.H.M. along the vertical direction is
A $2 π \sqrt{\frac{Y A}{m L}}$
B $2 π \sqrt{\frac{m L}{Y A}}$
C $2 π \sqrt{\frac{m Y}{A L}}$
D $2 π \sqrt{\frac{A L}{m Y}}$