A point mass starts moving in straight line with constant acceleration a from rest at t=0. At time t=2s, the acceleration changes the sign remaining the same in magnitude. The mass returns to the initial position at time t=t0 after start of motion. Here t0 is
4s
(4+2√2)s
(2+2√2)s
(4+4√2)s
The correct Answer is:B
To solve the problem step by step, we will analyze the motion of the point mass under the given conditions.
Step 1: Initial Setup
The point mass starts from rest at t=0 with a constant acceleration a. Therefore, the initial velocity u=0.
Step 2: Velocity After 2 Seconds
The velocity v of the mass at t=2 seconds can be calculated using the formula:
v=u+at
Substituting u=0 and t=2:
v=0+a⋅2=2a
Step 3: Change in Acceleration
At t=2 seconds, the acceleration changes its sign, becoming −a. The mass will now decelerate until it comes to rest.
Step 4: Time to Come to Rest
Let t′ be the time taken to come to rest after t=2 seconds. The final velocity vf=0 and initial velocity v=2a. Using the equation:
vf=v−at′
Substituting the values:
0=2a−at′
Rearranging gives:
at′=2a⟹t′=2 seconds
Step 5: Total Time Until Rest
The total time from the start until the mass comes to rest is:
ttotal=2+t′=2+2=4 seconds
Step 6: Distance Covered Until Rest
Now, we calculate the distance covered while moving with acceleration a for the first 2 seconds and then with acceleration −a for the next 2 seconds.
1. Distance during first 2 seconds:
s1=ut+12at2=0+12a(22)=2a
2. Distance during next 2 seconds (deceleration):
The initial velocity for this phase is 2a and the time is 2 seconds:
s2=vt′−12a(t′)2=(2a)(2)−12a(22)=4a−2a=2a
Step 7: Total Distance Covered
The total distance covered when the mass comes to rest is:
stotal=s1+s2=2a+2a=4a
Step 8: Return to Initial Position
After coming to rest, the mass will move back to the initial position. The distance to cover is 4a with a constant acceleration a (now positive).
Using the equation:
s=ut+12at2
Here, u=0 and s=4a:
4a=0+12at2return
Solving for treturn:
4a=12at2return⟹8=t2return⟹treturn=2√2 seconds
Step 9: Total Time t0
The total time t0 until the mass returns to the initial position is:
t0=4+2√2
Final Answer
Thus, the total time t0 is:
t0=4+2√2 seconds
The point mass starts from rest at t=0 with a constant acceleration a. Therefore, the initial velocity u=0.
The velocity v of the mass at t=2 seconds can be calculated using the formula:
v=u+at
Substituting u=0 and t=2:
v=0+a⋅2=2a
At t=2 seconds, the acceleration changes its sign, becoming −a. The mass will now decelerate until it comes to rest.
Let t′ be the time taken to come to rest after t=2 seconds. The final velocity vf=0 and initial velocity v=2a. Using the equation:
vf=v−at′
Substituting the values:
0=2a−at′
Rearranging gives:
at′=2a⟹t′=2 seconds
The total time from the start until the mass comes to rest is:
ttotal=2+t′=2+2=4 seconds
Now, we calculate the distance covered while moving with acceleration a for the first 2 seconds and then with acceleration −a for the next 2 seconds.
s1=ut+12at2=0+12a(22)=2a
The initial velocity for this phase is 2a and the time is 2 seconds:
s2=vt′−12a(t′)2=(2a)(2)−12a(22)=4a−2a=2a
The total distance covered when the mass comes to rest is:
stotal=s1+s2=2a+2a=4a
After coming to rest, the mass will move back to the initial position. The distance to cover is 4a with a constant acceleration a (now positive).
s=ut+12at2
Here, u=0 and s=4a:
4a=0+12at2return
Solving for treturn:
4a=12at2return⟹8=t2return⟹treturn=2√2 seconds
The total time t0 until the mass returns to the initial position is:
t0=4+2√2
Thus, the total time t0 is:
t0=4+2√2 seconds
Topper's Solved these Questions
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - MCQ_TYPE
27 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - COMPREHENSION_TYPE
19 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
11 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
Similar Questions
A point mass starts moving in a straight line with constant acceleration. After time t0 the acceleration changes its sign, remaining the same in magnitude. Determine the time T from the beginning of motion in which the point mass returns to the initial position.
View SolutionA point mass starts moving in a straight line with a constant acceleration a. At a time t1 a fter the beginning of motion, the acceleration changes sign, remaining the same in magnitude. Determine the time t from the beginning of motion in which the point mass returns to the initial position.
View Solution
Knowledge Check
A particle, initially at rest, starts moving in a straight line with an acceleration a=6t+4m/s2. The distance covered by it in 3 s is
A15 mB30 mC45 mD60 mA particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is
 A2m/sB3m/sC4m/sD6m/s
A2m/sB3m/sC4m/sD6m/sA body starts from rest at time t=0 , the acceleration time graph is shown in the figure . The maximum velocity attained by the body will be
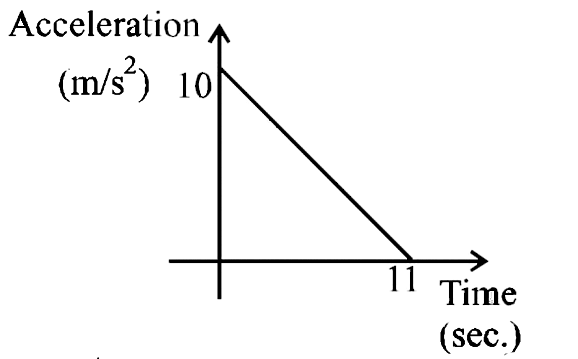 A110m/sB55m/sC650m/s(a)D550m/s
A110m/sB55m/sC650m/s(a)D550m/s
A particle, starting from rest, moves in a straight line with constant acceleration a0 for a time interval t0.Then is accelerates at a constant rate 2a0 for time interval 2t0 .The distance travelled by the particle in time 3t0 from the starts is S . Then Sa0t20=
View SolutionA particle starts with an initial velocity u towards +x direction with an acceleration a after time t1, it starts retarding with another acceleraation a', comes to an instantaneous stop and returns. If reaches its initial position at time t2. Draw the approximate time dependence plots for particle's displacement and velocity.
View SolutionA partical is moving in a straight line under constant acceleration 4m/s2. The motion starts from rest. Sketch v-t and s-t graph for the duration t=0 to t=5s.
View SolutionA particle starts moving from rest on a straight line. Its acceleration a verses time t is shown in the figure. The speed of the particle is maximum at the instant

View SolutionA particle starts from rest at t=0 and moves in a straight line with an acceleration as shown below. The velocity of the particle at t=3 s is

View Solution
