A point mass starts moving in a straight line with constant acceleration. After time t0 the acceleration changes its sign, remaining the same in magnitude. Determine the time T from the beginning of motion in which the point mass returns to the initial position.
The correct Answer is:A, C, D
If we start time calculation from point P and apply
the equation
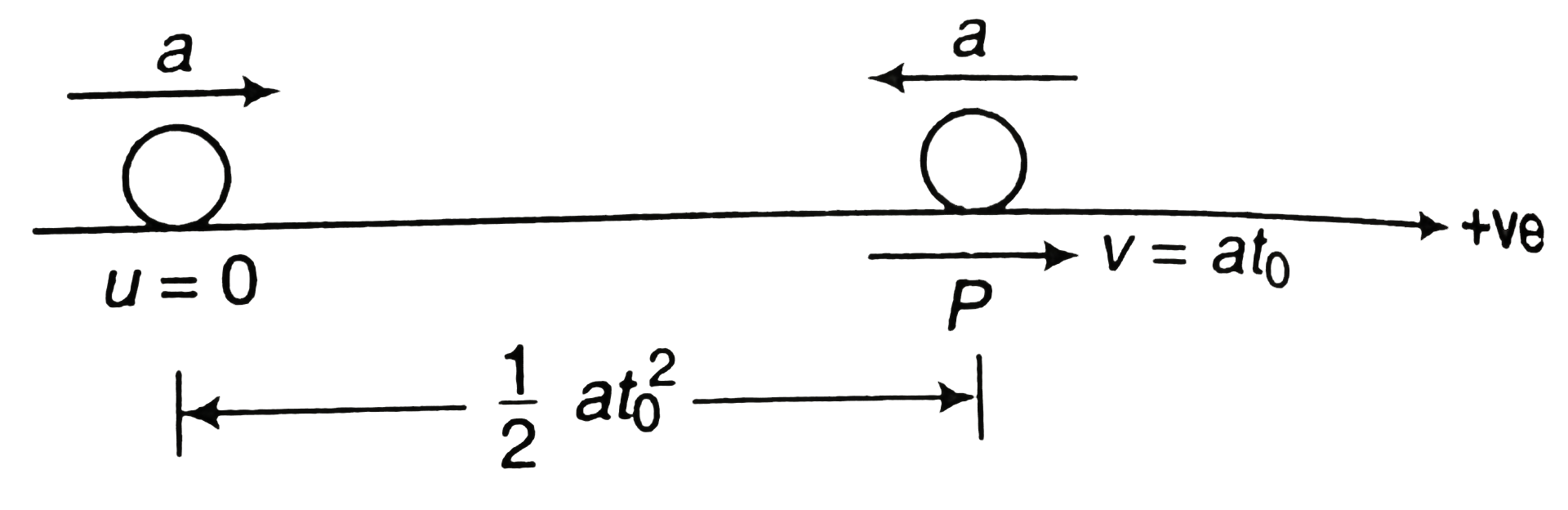
s=ut+12at2
(−12at20)=(+at0)t+12(−a)t2
Solving we get, t=(√2+1)t0
=2.414t0
∴ Total time, T=t+t0
=(3.414)t0
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - More Than One Correct6videos
KINEMATICS
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Comprehension7videos
KINEMATICS
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Objective45videos
KINEMATICS
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises45videos
GRAVITATION
- BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
Similar Questions
A point mass starts moving in a straight line with a constant acceleration a. At a time t1 a fter the beginning of motion, the acceleration changes sign, remaining the same in magnitude. Determine the time t from the beginning of motion in which the point mass returns to the initial position.
View SolutionA particle starts moving from rest on a straight line. Its acceleration a verses time t is shown in the figure. The speed of the particle is maximum at the instant
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A point mass starts moving in straight line with constant acceleration a from rest at t=0. At time t=2s, the acceleration changes the sign remaining the same in magnitude. The mass returns to the initial position at time t=t0 after start of motion. Here t0 is
A4sB(4+2√2)sC(2+2√2)sD(4+4√2)s - Question 2 - Select One
A body moving in a straight line with constant acceleration covers distances a and b in successive equal time interval of t. The acceleration of the body is
Aa+bt2Bb−at2C2b−a2t2Db−2at2 - Question 3 - Select One
A particle moves in a straight line and its position x at time t is given by x2=2+t. Its acceleration is given by :-
A−2x3B−14x3C−14x2D1x2
A point moves along a circle with a velocity v=t/2. Find the acceleration of the point at the moment when it has covered a quarter circle from the beginning of motion.
View SolutionA partical is moving in a straight line under constant acceleration 4m/s2. The motion starts from rest. Sketch v-t and s-t graph for the duration t=0 to t=5s.
View SolutionA particle of mass m is moving along the line y-b with constant acceleration a. The areal velocity of the position vector of the particle at time t is (u=0)
View SolutionA particle starts moving from rest in a from rest in a straight line. Its acceleration vs time (a−t) graph is shown in figure. The speed of particle is maximum at.
 View Solution
View SolutionA body lying initially at point (3,7) starts moving with a constant acceleration of 4ˆi. Its position after 3s is given by the coordinates
View Solution

