A point object O is placed in fornt of a transparent slab at a distance x from its surface. It is seenfrom the other side of he slab by light incident nearlyl normally to the slab. The thickness of the slab is t and its refractive index is μ. Show that the apparent shift in the position of the object is independent of x and find its value.
 <br> The situatiojn is shown in ure Because of the refraction at the first surface, the image of O is formed at <span class=) O1. For the refraction, the real depth is AO=x and the apparent depth is AO1. Also the first medium is air and the second is the slab. Thus
O1. For the refraction, the real depth is AO=x and the apparent depth is AO1. Also the first medium is air and the second is the slab. Thus
xAO1=1μorAO1=μx
The point O1 acts as the object for the refraction at the second surface. Due to this refraction the image of O2 is formed at I. Thus,
BO1BI=μ
orAB+AO1BI=μort−μxBI=μ
orBI=x+tμ
The≠tshift∈OI=OB−BI=(x+t)−(x+tμ)
=t(1−1μ)
which is independent of x.
Similar Questions
A ray of light is incident at an angle of 60° on a parallel side of a glass slab of thickness 0.1 m and refractive index 1.5. Calculate the lateral shift produced.
View SolutionA ray of light strikes the glass slab at an angle of 90∘ from its surface. What is the angle of incidence and the angle of refraction ?
View Solution
Knowledge Check
If t is the real thickness μ is refractive index of a glass slab then the shift of the image with refernce to the object is given by
At[1−μ]Bt[1−1μ]Ct[μ−1]Dt[1μ−1]An object is seen through a glass slab of thickness 36cm and refractive index 3/2. The observer, and the slab are dipped in water (μ=4/3). The shift produced in the position of the object is
A12cmB4cmC6cmD8cmA point object is placed in front of a concave mirror. And its image is found to coincide with its own position. Now a glass slab of thickness 15 cm and refractive index 1.5 is placed in between object and the mirror. In order to form image again at the location of object, it is required to move the object
Atowards the mirror by 5 cmBaway from the mirror by 5 cmCtowards the mirror by 7.5 cmDaway from mirror by 7.5 cm
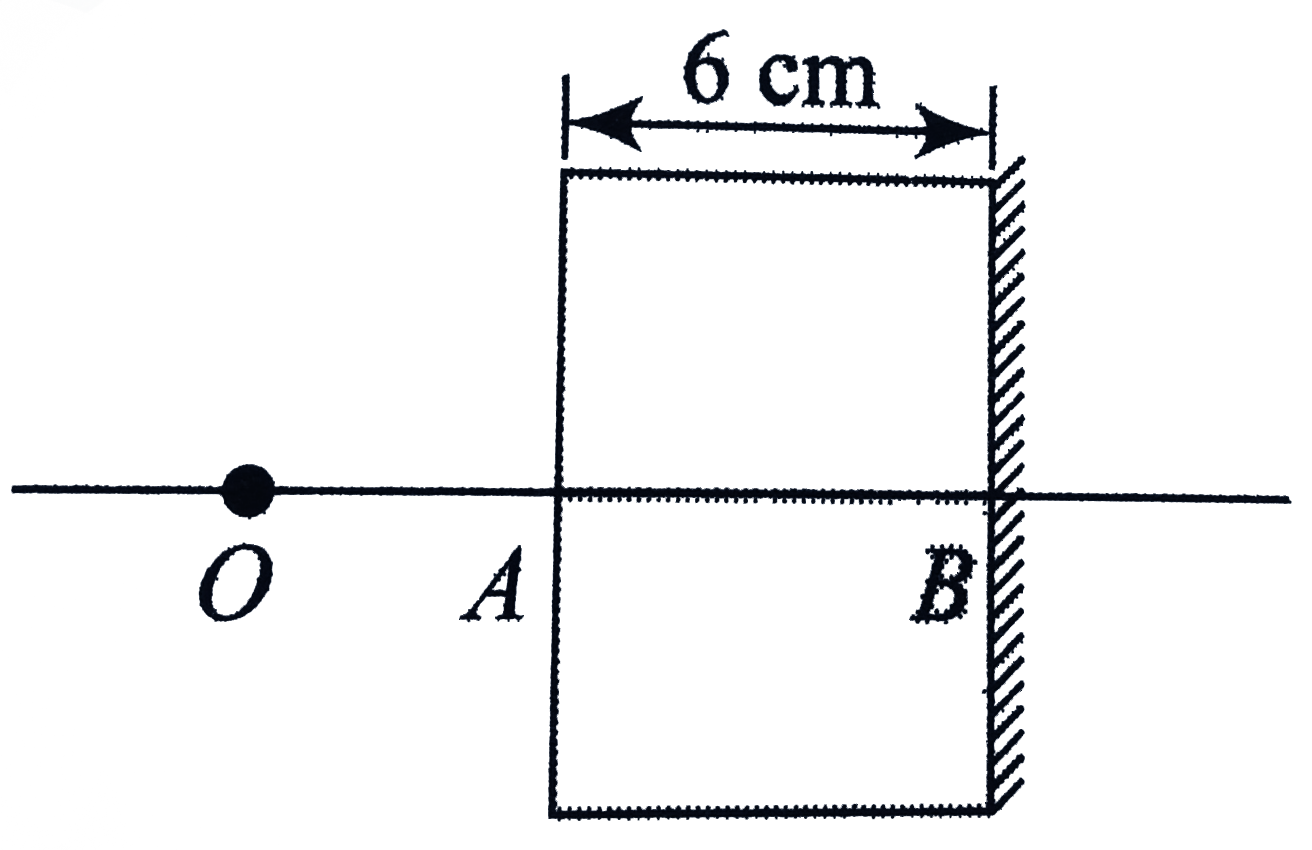
An object O is placed at 8cm in front of a glass slab, whose one face is silvered as shown in Figure. The thickness of the slab is 6cm. If the image formed 10 cm behind the silvered face, find the refractive index of glass.
View SolutionA point object (A) is kept at a distance (L) from a convex mirror on its principal axis. A glass slab is inserted between the object and the mirror with its refracting surfaces perpendicular to the principal axis of the mirror. The thickness of the slab is 6 cm and its refractive index is 32. The image formed after refraction through the slab, reflection from the mirror followed by refraction through the slab is a virtual image at a distance of 10 cm from the pole of the mirror (on its principal axis). Consider paraxial rays only and calculate the distance (L) of the object from the mirror. Focal length of the mirror is f=20cm.

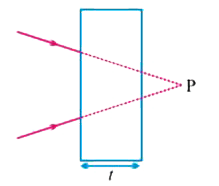
View SolutionA converging beam of light is intercepted by a slab of thickness t andrefractive index μ, By what distance will the convergence point be shiffted? Illustrate the answer.
View SolutionIn YDSE when slab of thickness t and refractive index μ is placed in front of one slit then central maxima shifts by one fringe width. Find out t in terms of λ and μ.
View SolutionA slab of transparent material is made as shown in Fig. Monochromatic parallel beams of light are normally incident on the slab. The thickness of C is twice the thickness of B. If the number of waves in A = number of waves in combination of BandC, then the refractive index of B is :
 .
.
View Solution