A rectangular slab of refractive index μ is placed on another slab of refractive index 3. Both the slabs are of the same dimensions. There is a coin at the bottom of the lower slab. What should be the value of μ such that when viewed normally from above, the coin appears to be at the surface of separation of the two slabs?
Let thickness of each slab be d. According to the question the apparent depth of the coin = d.
∴ d=dμ+d3or,1=1μ+13
or, 1μ=23or,μ=32=1.5
Topper's Solved these Questions
- BOOK - CHHAYA PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - HIGHER ORDER THINKING SKILL (HOTS QUESTION)25videos
REFRACTION OF LIGHT
- BOOK - CHHAYA PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - SECTION RELATED QUESTION18videos
REFRACTION OF LIGHT
- BOOK - CHHAYA PUBLICATIONCHAPTER - REFLECTION OF LIGHTEXERCISE - INTEGER ANSWER TYPE3videos
REFLECTION OF LIGHT
- BOOK - CHHAYA PUBLICATIONCHAPTER - SEMICONDUCTORS AND ELECTRONICS EXERCISE - CBSE SCANNER31videos
SEMICONDUCTORS AND ELECTRONICS
Similar Questions
A rectangular slab of refractive index mu is placed over another slab of refractive index 3 both slabs being identical in dimensions.If a coin is placed below the lower slab for what value of mu will the coin appear to be placed at the interface between the slabs when viewed from the top
View SolutionA slab of water is on the top of a glass slab of refractive index 2. At what angle to the normal must a ray be incident on the top sureface of th eglass slab so that it is reflected from the bottom surface as shown in figure ?
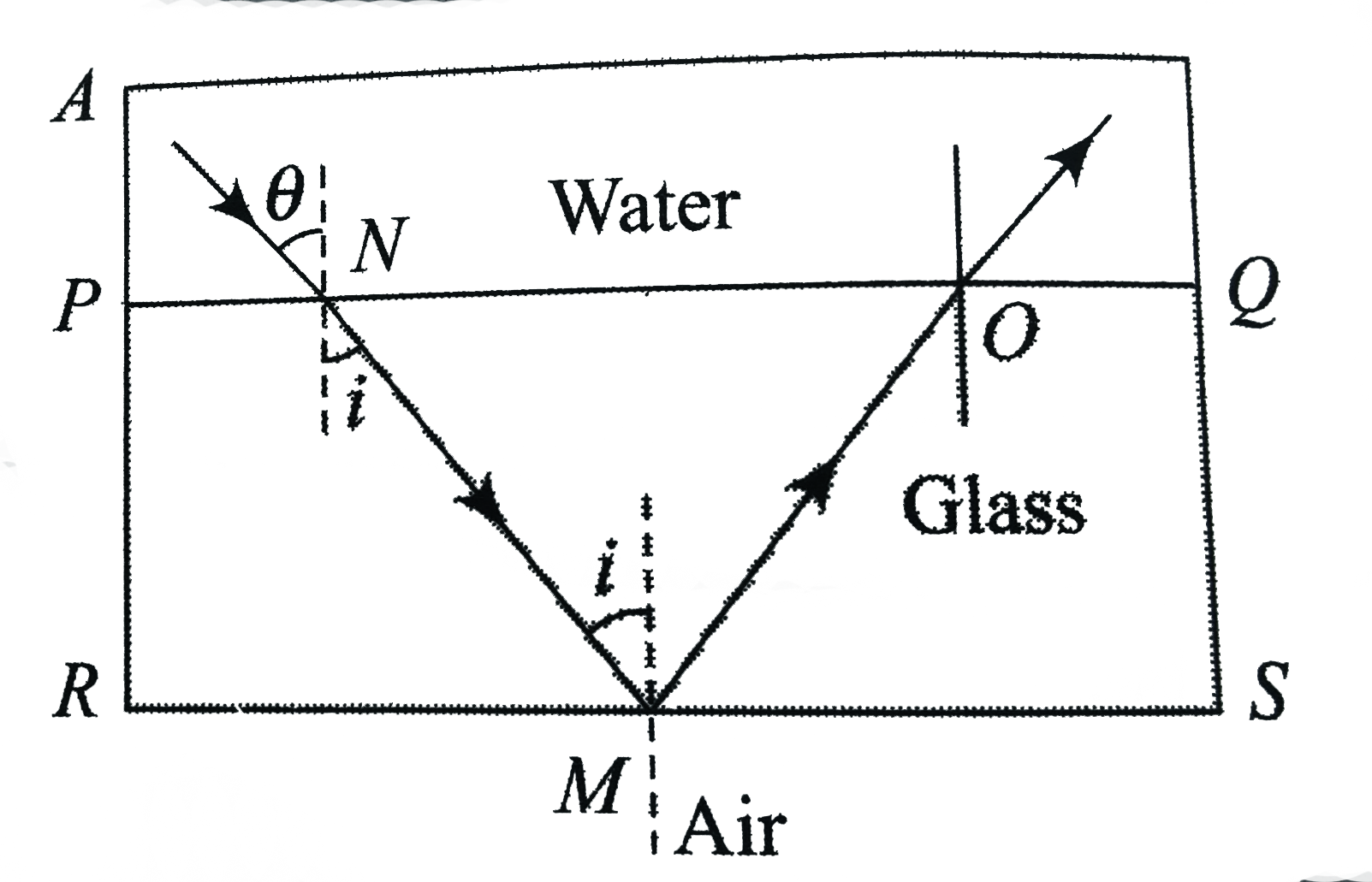 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A rectangular glass slab ABCD of refractive index n1 is immersed in water of refractive index n2(n1<n2). A ray of light is incident at the surface AB of the slab as shwon. The maximum value of the angle of incidence αmax such that the ray comes out from the other surface CD is given by
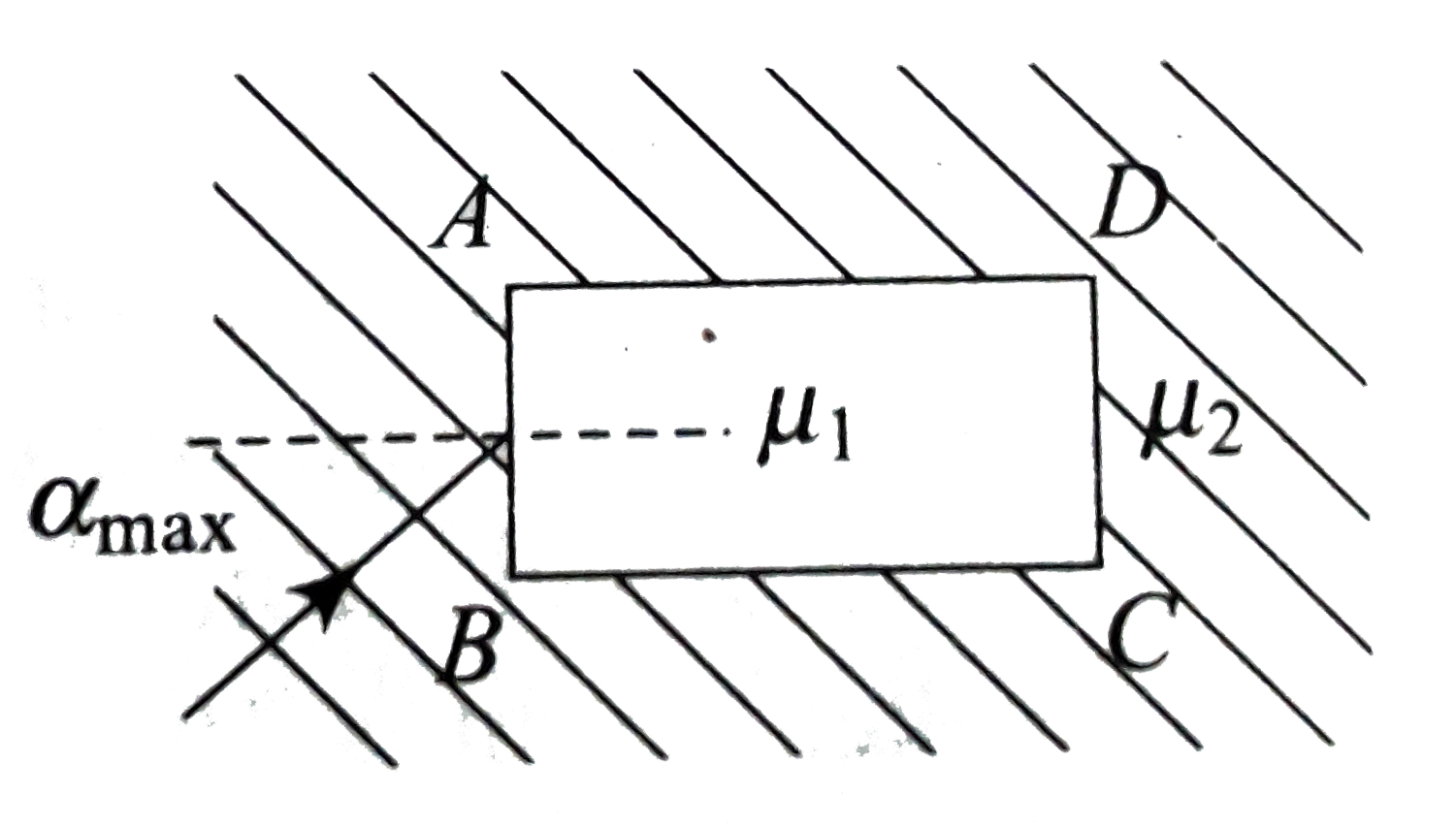 Asin−1[n1n2cos(sin−1(n2n1))]Bsin−1[n1cos(sin−1(1n2))]Csin−1(n1n2)Dsin−1(n2n1)
Asin−1[n1n2cos(sin−1(n2n1))]Bsin−1[n1cos(sin−1(1n2))]Csin−1(n1n2)Dsin−1(n2n1) - Question 2 - Select One
Find the distance of object placed in the slab of refractive index μ from point P of the curved surface of radius R so that image is formed at infinity:
 A(μ−1)RμBμR(μ−1)CR(μ−1)D(μ−1)R2μ
A(μ−1)RμBμR(μ−1)CR(μ−1)D(μ−1)R2μ - Question 3 - Select One
A spot is placed on the bottom of a slab made of transperent material of refractive index 1.5. The spot is viewed vertically from the top when it seems to be raised by 2 cm. Then, the height of the slab is
A10 cmB8 cmC6 cmD4 cm
A slab of water is on the top of a glass slab of refractive index 2. At what angle to the normal must a ray be incident on the top sureface of th eglass slab so that it is reflected from the bottom surface as shown in figure ?
 View Solution
View SolutionFind the distance of object placed in the slab of refractive index μ from point P of the curved surface of radius R so that image is formed at infinity:
 View Solution
View SolutionA spot is placed on the bottom of a slab made of transperent material of refractive index 1.5. The spot is viewed vertically from the top when it seems to be raised by 2 cm. Then, the height of the slab is
View SolutionA ray of light is incident on a glass slab at grazing incidence. The refractive index of the material of the slab is given by μ=√(1+y) . If the thickness of the slab is d=2m, determing the equation of the trajectory of the ray inside the slab and the coordinates of the point where the ray exits from the slab. Take the origin to be at the point of entry of the ray.
View SolutionA ray of light is incident on a glass slab at grazing incidence. The refractive index of the material of the slab is given by μ=√1+√y. If the thickness of the slab is d, determine the equation ofthe trajectory of the ray inside the slab and the coordinates of the point where the ray exits from the slab. Take the origin to be at the point of entry of the ray.
View Solution

