A police inspector in a jeepis chasing a pickpocket on a straightroad. The jeep is going at its maximum speed v (assumed uniform). The pickpocket rides on the motorcycle of a waiting friend when the jeepis at a distance of a waiting friend when the jeep is at a distance d away, and the motorcycle starts with a constant acceleration a. Show that the pickpocket will be caught it v≥√2ad.
To solve the problem of the police inspector in a jeep chasing a pickpocket on a motorcycle, we can break it down into a series of steps using the equations of motion.
1. Understanding the Scenario:
- The jeep is moving at a constant speed v.
- The pickpocket starts from rest on a motorcycle with a constant acceleration a.
- The initial distance between the jeep and the pickpocket is d.
2. Setting Up the Equations:
- For the pickpocket on the motorcycle, the distance traveled d can be described using the second equation of motion:
d=ut+12at2
Here, u=0 (initial velocity of the motorcycle), so the equation simplifies to:
d=12at2
3. Distance Covered by the Jeep:
- The distance covered by the jeep in the same time t is:
Distancejeep=vt
4. Setting the Distances Equal:
- For the pickpocket to be caught, the distance covered by the jeep must equal the distance the pickpocket has traveled plus the initial distance d:
vt=d+12at2
5. Rearranging the Equation:
- Rearranging gives:
12at2−vt+d=0
6. Using the Quadratic Formula:
- This is a quadratic equation in t. We can use the quadratic formula:
t=−b±√b2−4ac2a
Here, a=12a, b=−v, and c=d:
t=v±√v2−2ada
7. Condition for Real Solutions:
- For the pickpocket to be caught, the term under the square root must be non-negative:
v2−2ad≥0
This simplifies to:
v2≥2ad
8. Final Result:
- Taking the square root of both sides gives:
v≥√2ad
- Thus, the condition for the pickpocket to be caught is:
v≥√2ad
- The jeep is moving at a constant speed v.
- The pickpocket starts from rest on a motorcycle with a constant acceleration a.
- The initial distance between the jeep and the pickpocket is d.
- For the pickpocket on the motorcycle, the distance traveled d can be described using the second equation of motion:
d=ut+12at2
Here, u=0 (initial velocity of the motorcycle), so the equation simplifies to:
d=12at2
- The distance covered by the jeep in the same time t is:
Distancejeep=vt
- For the pickpocket to be caught, the distance covered by the jeep must equal the distance the pickpocket has traveled plus the initial distance d:
vt=d+12at2
- Rearranging gives:
12at2−vt+d=0
- This is a quadratic equation in t. We can use the quadratic formula:
t=−b±√b2−4ac2a
Here, a=12a, b=−v, and c=d:
t=v±√v2−2ada
- For the pickpocket to be caught, the term under the square root must be non-negative:
v2−2ad≥0
This simplifies to:
v2≥2ad
- Taking the square root of both sides gives:
v≥√2ad
- Thus, the condition for the pickpocket to be caught is:
v≥√2ad
Topper's Solved these Questions
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Objective -1
13 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Objective -2
9 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer
13 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer
14 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
Similar Questions
A police inspector is chasing a thief who is running away in a car with a speed 3m/s. The speed of police jeep is 12 m/s. Then the speed of image of police jeep as seen by thief in the rear view mirror when the police jeep is at a distance of 30 m is (value of focal length of the rear view mirror is 15 m)
View SolutionAn accelration produces a narrow beam of protons, each having an initial speed of v0. The beam is directed towards an initially uncharges distant metal sphere of radius R and centered at point O. The initial path of the beam is parallel to the axis of the sphere at a distance of (R/2) from the axis, as indicated in the diagram.

The protons in the beam that collide with the sphere will cause it to becomes charged. The subsequentpotential field at the accelerator due to the sphere can be neglected. The angular momentum of a particle is defined in a similar way to the moment of a force. It is defined as the moment of its linear momentum, linear replacing the force. We may assume the angular momentum of a proton about point O to be conserved. Assume the mass of the proton as mP and the charge on it as e. Given that the potential of the sphere increases with time and eventually reaches a constant velue.
After a long time, when the potential of the sphere reaches a constant value, the trajectory of proton is correctly sketched as

View Solution
Knowledge Check
A police party is chasing a dacoit in a jeep which is moving at a constant speed v. The dacoit is on a motor cycle. When he is at a distance x from the jeep, he accelerates from rest at a constant rate α. Which of the following relations is true, if the police is able to catch the dacoit ?
Av2<axBv2<2axCv2≥2axDv2=ax
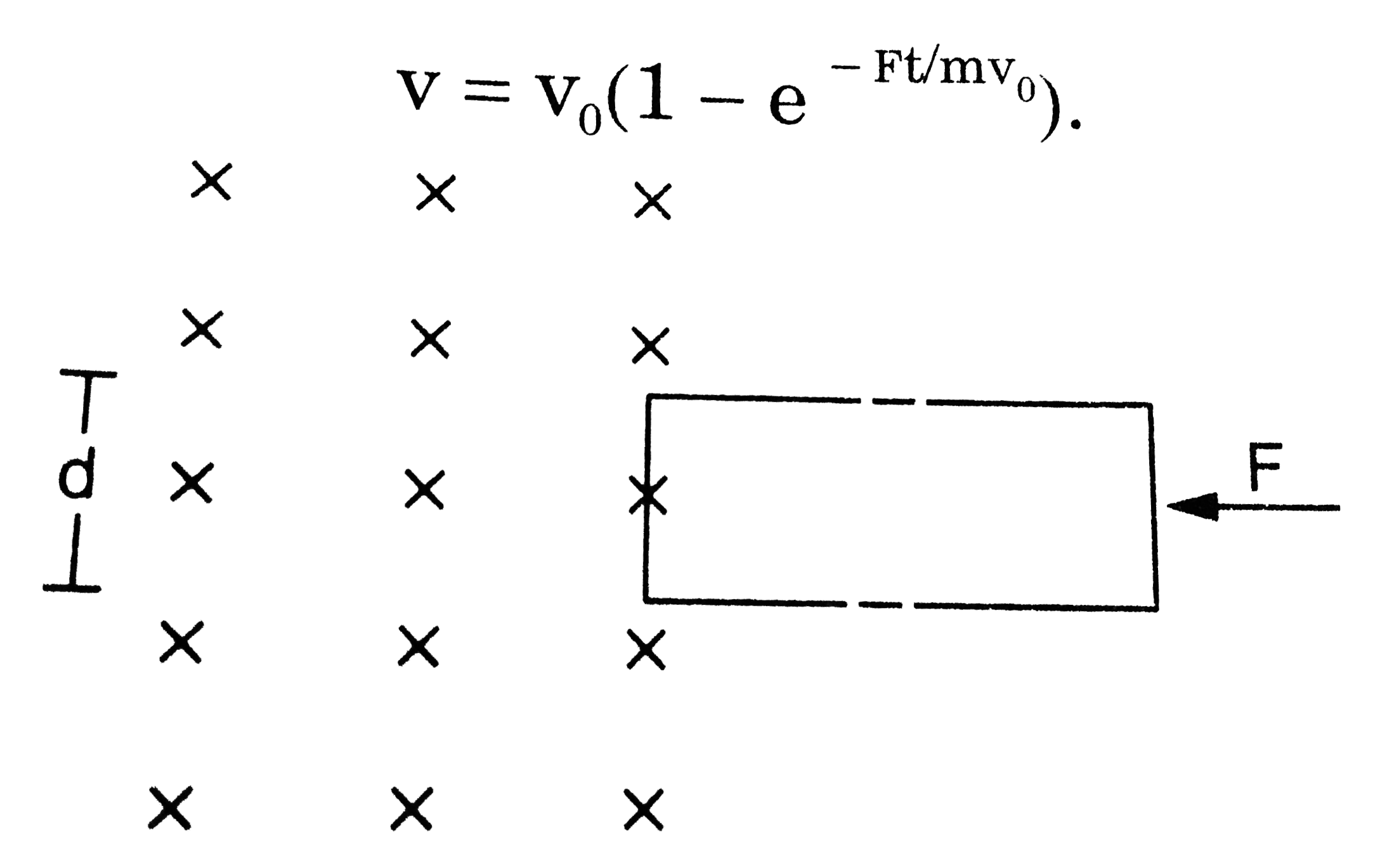
The rectangualr wire- frame, shown in has a width d, mass m, resistance R and a large length. A uniform magnetic field B exists to the left of the frame. A constant force F starts pushing the frame into the magnetic field at t =0. (a) Find the acceleration of the frame when its speed has increased to v. (b) Show that after some time the frame will move with a constant velocity till the whole frame enters into the magnetic field. find this velocity v0. (c) show that the velocity at tiem t is given by v=v0(1−e−Ftmv0.
View SolutionRam and Ali have been fast friends since childhood. Ali neglected studies and now has no means to earn money other than a channel whereas Ram has become an engineer. Now both are working in the same factory. Ali uses camel to transport the load within the factory.
 Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
i. The load used in each trip is 1000kg and has friction coefficient μk=0.1 and μs=0.2.
ii. Mass of camel is 500kg.
iii. Load is accelerated for first 50m with constant acceleration, then it is pulled at a constant speed of 5ms−1 for 2km and at last stopped with constant retardation in 50m.
iv. From biological data, the rate of consumption of energy of camel can be expressed as P=18×103v+104Js−1 where P is the power and v is the velocity of the camel. After calculations on different issues, Ram suggested proper food, speed of camel, etc. to his friend. For the welfare of Ali, Ram wrote a letter to the management to increase his salary.
(Assuming that the camel exerts a horizontal force on the load):
The ratio of the energy consumed by the camel during uniform motion for the two cases when it moves with speed 5ms−1 to the case when it moves with 10ms−1
View SolutionAt the instant, the traffic light turns green, a car that has been waiting at an intersection starts ahead with a constant acceleration of 3.20ms−2, At the some instant, a truck travelling with a constant speed of 20.0ms−1, overtakes and passes the car.
a. At what distance from its starting point does the car overtake the truck?
b. Calculate the speed of the car when it overtakes the truck.
c. Sketch an x−t graph of themotion of both vehicles.
Take x−0 at the intersection.
d. Sketch a vx−t graph of the motion of both vehicles.
View SolutionState Faraday's law of electromagnetic induction.
Figure shows a rectangular conductor PQRS in which the conductor PQ is free to move in a uniform magnetic field B perpendicular to the plane of the paper.The field extends from x=0 to x=b and is zero for x>b.Assume that only the arm PQ posses resistance r.When the arm PQ is pulled outward from x=0 with constant speed v, obtain the expressions for the flux and the induced emf. sketch the variations of these quantities with distance 0≤x≤2b.

View SolutionA student is running at her top speed of 5.0ms−1, to catch a bus, which is stopped at the bus stop. When the student is still 40.0m from the bus, it starts to pull away, moving with a constant acceleration of 0.2ms−2.
a For how much time and what distance does the student have to run at 5.0ms−1 before she overtakes the bus?
b. When she reached the bus, how fast was the bus travelling?
c. Sketch an x−t graph for bothe the student and the bus.
d. Teh equations uou used in part (a)to find the time have a second solution, corresponding to a later time for which the student and the bus are again at thesame place if they continue their specified motions. Explain the significance of this second solution. How fast is the bus travelling at this point?
e. If the students⊤speedis3.5 m s^(-1), will she catch the bus?
f. What is the minimum speed the student must have to just catch up with the bus?For what time and what distance dies she have to run in that case?
View Solution
