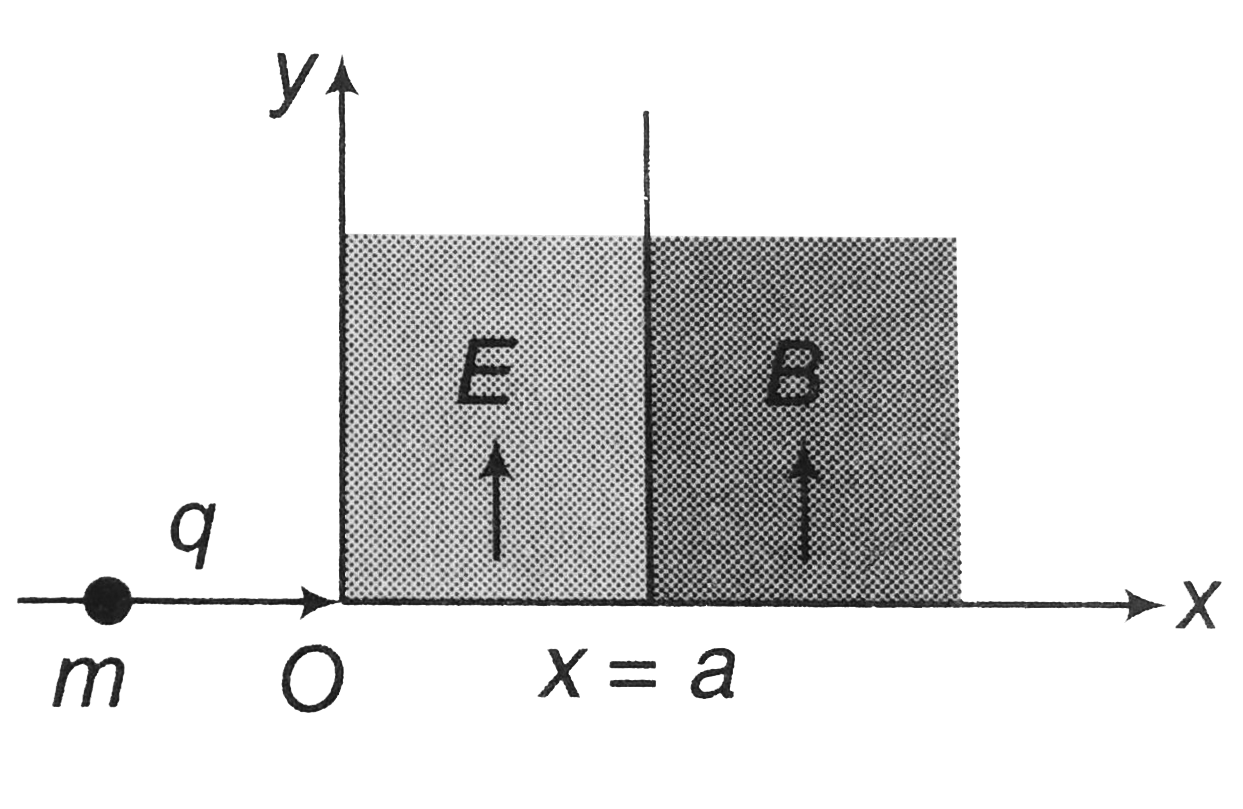
A positively charged particle having charge q is accelerated by a potential difference V. This particle moving along the x-axis enters a region where an electric field E exists. The direction of the electric field is along positive y-axis. The electric field exists in the region bounded by the lines x=0 and x=a. Beyond the line x=a (i.e. in the regionx≥a there exists a magnetic field of strength B, directed along the positive y-axis. Find
(a) at which point does the particle meet the line x=a
(b) the pitch of the helix formed after the particle enters the region x ?_ a. Mass of the particle is m.
The correct Answer is:(a) (x,y)=(a,14Ea2V); (b) p=πaEB(2mVq)1/2
The work done by the potential difference gets stored as its kinetic
energy.
∴12mv2=qV⇒v=(2qVm)1/2....(i)
(a) When it enters the region xε[0,a), it experiences an electric
field →E=Eˆj
Time taken to cross the region:vt=a
⇒t=av=a(m2qV)1/2....(ii)
The distance travelled in y-direction during this time is
y=12qEmt2=12×qEm×a2×m2qV
⇒y=14Ea2V
Hence, the particle meets the line x=a at point
(x,y)=(a,14Ea2V)
(b) Now, velocity of the particle as it crosess the line x=a
→v=(2qVm)1/2ˆi+qEm(2qVm)1/2ˆj
Magnetic field in this region, →B=B→j
Hence, the time period of revolution ,t=2πmqB
Pitch P=v∣∣t=2πmmqB×aE(mq2V)1/2
P=πaEB(2mVq)1/2.
Topper's Solved these Questions
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Single Correct
70 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercises Multiple Correct
25 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Exercise1.3
14 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
- MISCELLANEOUS VOLUME 3BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False
3 Videos
Similar Questions
A positively charged particle, having charge q, is accelerated by a potential difference V. This particle moving along the x-axis enters a region where an electric field E exists. The direction of the electric field is along positive y-axis. The electric field exists in the region bounded by the lines x=0andx=a. Beyond the line x=a (i.e., in the region x>a), there exists a magnetic field of strength B, directed along the positive y-axis. Find

a. at which point does the particle meet the line x=a.
b. the pitch of the helix formed after the particle enters the region x≥a. (Mass of the particle is m.)
View SolutionA positively charged particle moving along x-axis with a certain velocity enters a uniform electric field directed along positive y-axis. Its
View SolutionAn electron moving with a speed u along the positive x-axis at y=0 enters a region of uniform magnetic field which exists to the right of y-axis. The electron exits from the region after some time with the speed v at coordinate y, then

View SolutionAn electron moving with a speed u along the positive x-axis at y=0 enters a region of uniform magnetic field which exists to the right of y-axis. The electron exits from the region after some time with the speed v at coordinate y, then

View SolutionA moving charged particle q travelling along the positive X-axis enters a uniform magnetic field B. When will the force acting on q be maximum?
View SolutionAn electric dipole is placed at origin in the xy plane with its orientation along the positive x-axis. The direction is electric field .
View SolutionA charge q moves region in a electric field E and the magnetic field B both exist, then the force on its is
View SolutionA charged particle is at rest in the region where magnetic field and electric field are parallel. The particle will move in a
View SolutionThe magnetic field exists along negative x-axis and electric field exists along positive x-axis. A charged particle moves with a velocity inclined at an angle (θ) with vertical in (x-y) plane. What will be the correct diagram of the helical path?
View SolutionAn electron is moving along positive x-axis A unifrom electric field exists towards negative y-axis. What should be the direction of magnetic field of suitable magnitude so that net force of electrons is zero .
View Solution
