An electron is moving along positive x-axis A unifrom electric field exists towards negative y-axis. What should be the direction of magnetic field of suitable magnitude so that net force of electrons is zero .
positive z- axis
negative z-axis
positive y-axis
negative y-axis
The correct Answer is:B
To solve the problem, we need to analyze the forces acting on the electron and determine the direction of the magnetic field that will result in a net force of zero. Here’s a step-by-step breakdown of the solution:
Step 1: Identify the Forces Acting on the Electron
The electron is subject to two forces:
1. Electric Force (F_E): This force is due to the electric field (E) and is given by the equation:
FE=qE
where q is the charge of the electron (which is negative).
2. Magnetic Force (F_B): This force is due to the magnetic field (B) and is given by the equation:
FB=q(v×B)
where v is the velocity of the electron.
Step 2: Determine the Direction of the Electric Field
The problem states that there is a uniform electric field directed towards the negative y-axis. Therefore, we can represent the electric field as:
E=−E^j
This means the electric force on the electron (which has a negative charge) will be directed in the positive y-direction:
FE=qE=−e(−E^j)=eE^j
Step 3: Determine the Direction of the Velocity
The electron is moving along the positive x-axis, so we can represent its velocity as:
v=v^i
Step 4: Set Up the Condition for Zero Net Force
For the net force on the electron to be zero, the sum of the electric force and the magnetic force must equal zero:
FE+FB=0
This implies:
FB=−FE
Step 5: Calculate the Magnetic Force
The magnetic force can be expressed as:
FB=q(v×B)=−e(v×B)
Substituting the expressions for v and B:
FB=−e(v^i×B)
Step 6: Determine the Direction of the Magnetic Field
To find the direction of B, we need v×B to point in the direction of −FE, which is in the positive y-direction (^j).
Using the right-hand rule for the cross product:
- Point your fingers in the direction of v (positive x-axis).
- Curl your fingers towards the direction of ^j (positive y-axis).
This means your thumb (which represents the direction of B) must point in the negative z-direction (−^k). Therefore, we conclude:
B=−B^k
Step 7: Conclusion
The direction of the magnetic field should be in the negative z-direction (or −^k) to ensure that the net force on the electron is zero.
The electron is subject to two forces:
1. Electric Force (F_E): This force is due to the electric field (E) and is given by the equation:
FE=qE
where q is the charge of the electron (which is negative).
FB=q(v×B)
where v is the velocity of the electron.
The problem states that there is a uniform electric field directed towards the negative y-axis. Therefore, we can represent the electric field as:
E=−E^j
This means the electric force on the electron (which has a negative charge) will be directed in the positive y-direction:
FE=qE=−e(−E^j)=eE^j
The electron is moving along the positive x-axis, so we can represent its velocity as:
v=v^i
For the net force on the electron to be zero, the sum of the electric force and the magnetic force must equal zero:
FE+FB=0
This implies:
FB=−FE
The magnetic force can be expressed as:
FB=q(v×B)=−e(v×B)
Substituting the expressions for v and B:
FB=−e(v^i×B)
To find the direction of B, we need v×B to point in the direction of −FE, which is in the positive y-direction (^j).
- Point your fingers in the direction of v (positive x-axis).
- Curl your fingers towards the direction of ^j (positive y-axis).
B=−B^k
The direction of the magnetic field should be in the negative z-direction (or −^k) to ensure that the net force on the electron is zero.
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Only One Option is Correct
45 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - More than One Option is Correct
25 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
- MEASUREMENT AND ERRORSBOOK - DC PANDEY ENGLISHCHAPTER - MEASUREMENT AND ERRORSEXERCISE - Subjective
19 Videos
Similar Questions
An electron beam projected along + X-axis, experience a force due to a magnetic field along the + Y-axis. What is the direction of the magnetic field?
View SolutionAn electron is projected along positive z-axis, magnetic field is present along y-axis then direction of initial acceleration of the particle is
View Solution
Knowledge Check
Assertion : In a uniform electric field electrons move in the opposite direction of electric field.
Reason : This is because of the negative charge of an electron.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.
An electron beam projected along positive x-axis deflects along the positive y-axis. If this deflection is caused by a magnetic field, what is the direction of the field?
View SolutionA beam of α particles projected along + x-axis, experiences a force due to a magnetic field along the +y-axis figure. What is the direction of magnetic field.
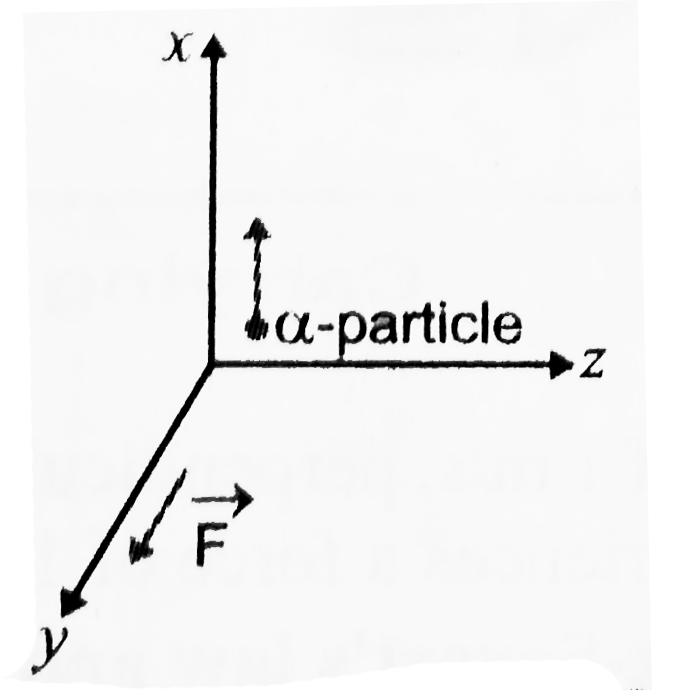
View SolutionAn electron is moving along the positive x-axis. You want to apply a magnetic field for a short time so that the electron may reverse its direction and move parallel to the nagative x-axis. This can be done by applying the magnetic field along
View SolutionAn electron beam projected along the positive x-axis deflects along the positive y-axis deflects . If this deflection is caused by a magnetic field, what is the direction of the field? Can we conclude that is parallel to the z-axis?
View SolutionAn electron is moving along positive x-axis. To get it moving on an anticlockwise circular path in x-y plane, a magnetic field is applied
View SolutionAn electron is moving along positive x-axis. To get it moving on an anticlockwise circular path in x-y plane, a magnetic field is applied
View SolutionAn electron moving with a speed u along the positive x-axis at y=0 enters a region of uniform magnetic field which exists to the right of y-axis. The electron exits from the region after some time with the speed v at coordinate y, then

View Solution
