A positively charged thin metal ring of radius R is fixed in the xy plane with its centre at the origin O. A negatively charged particle P is released from rest at the point (0,0,z0) where z0>0. Then the motion of P is
periodic, for all values of z0 satisfying 0<z0<∞.
simple harmonic, for all values of z0 satisfying 0<z0≤R
approximately simple harmonic, provided z0<<R
such that P crosses O and continues to move along the negative z-axis toward z=−∞.
To solve the problem, we need to analyze the motion of a negatively charged particle P released from rest at the point (0,0,z0) in the presence of a positively charged thin metal ring located in the xy-plane at the origin.
1. Understanding the Setup:
- We have a positively charged ring with radius R lying in the xy-plane, centered at the origin O(0,0,0).
- A negatively charged particle P is placed at the point (0,0,z0) where z0>0.
2. Electric Field Due to the Ring:
- The electric field E at point P due to the charged ring can be derived using the formula for the electric field along the axis of a charged ring:
E=14πϵ0⋅Qz0(R2+z20)3/2
- Here, Q is the total charge on the ring, R is the radius of the ring, and z0 is the distance from the center of the ring to the point P.
3. Direction of the Electric Field:
- Since the ring is positively charged, the electric field E at point P will point away from the ring, which means it will be directed along the positive z-axis towards the point P.
4. Force on the Negatively Charged Particle:
- The force F acting on the negatively charged particle P can be calculated using:
F=q⋅E
- Here, q is the charge of the particle P (which is negative), and E is the electric field calculated above.
- The force will thus be directed towards the ring (downwards along the z-axis) since the charge q is negative.
5. Motion of the Particle:
- As the particle P is released from rest, it will experience a force directed towards the center of the ring. This force is proportional to the displacement from the equilibrium position (the center of the ring).
- If we consider small displacements (i.e., if z0 is much smaller than R), the motion can be approximated as simple harmonic motion (SHM) because the restoring force is proportional to the displacement.
6. Conclusion:
- Therefore, the motion of the negatively charged particle P will be simple harmonic motion as it oscillates about the center of the ring due to the attractive force exerted by the positively charged ring.
Final Answer:
The motion of the negatively charged particle P will be simple harmonic motion.
- We have a positively charged ring with radius R lying in the xy-plane, centered at the origin O(0,0,0).
- A negatively charged particle P is placed at the point (0,0,z0) where z0>0.
- The electric field E at point P due to the charged ring can be derived using the formula for the electric field along the axis of a charged ring:
E=14πϵ0⋅Qz0(R2+z20)3/2
- Here, Q is the total charge on the ring, R is the radius of the ring, and z0 is the distance from the center of the ring to the point P.
- Since the ring is positively charged, the electric field E at point P will point away from the ring, which means it will be directed along the positive z-axis towards the point P.
- The force F acting on the negatively charged particle P can be calculated using:
F=q⋅E
- Here, q is the charge of the particle P (which is negative), and E is the electric field calculated above.
- The force will thus be directed towards the ring (downwards along the z-axis) since the charge q is negative.
- As the particle P is released from rest, it will experience a force directed towards the center of the ring. This force is proportional to the displacement from the equilibrium position (the center of the ring).
- If we consider small displacements (i.e., if z0 is much smaller than R), the motion can be approximated as simple harmonic motion (SHM) because the restoring force is proportional to the displacement.
- Therefore, the motion of the negatively charged particle P will be simple harmonic motion as it oscillates about the center of the ring due to the attractive force exerted by the positively charged ring.
The motion of the negatively charged particle P will be simple harmonic motion.
Similar Questions
A positively charged ring is in y - z plane with its centre at origin . A positive test charge qe , held at origin is released along x axis, then its speed
View SolutionA circular ring of radius R with uniform positive charge density λ per unit length is located in the y z plane with its center at the origin O. A particle of mass m and positive charge q is projected from that point p(−√3R,0,0) on the negative x - axis directly toward O, with initial speed V. Find the smallest (nonzero) value of the speed such that the particle does not return to P ?
View SolutionA circular ring of radius R and uniform linear charge density +λC/m are kept in x - y plane with its centre at the origin. The electric field at a point (0,0,R√2) is
View SolutionThe gravitational force →F upon an object of mass m placed in external gravitational field →Eext is given by →F=m→Eext. Consider a fixed mass ring (of mass M, radius R) in y-z plane, with centre at (0,0) and axis of ring along x direction.
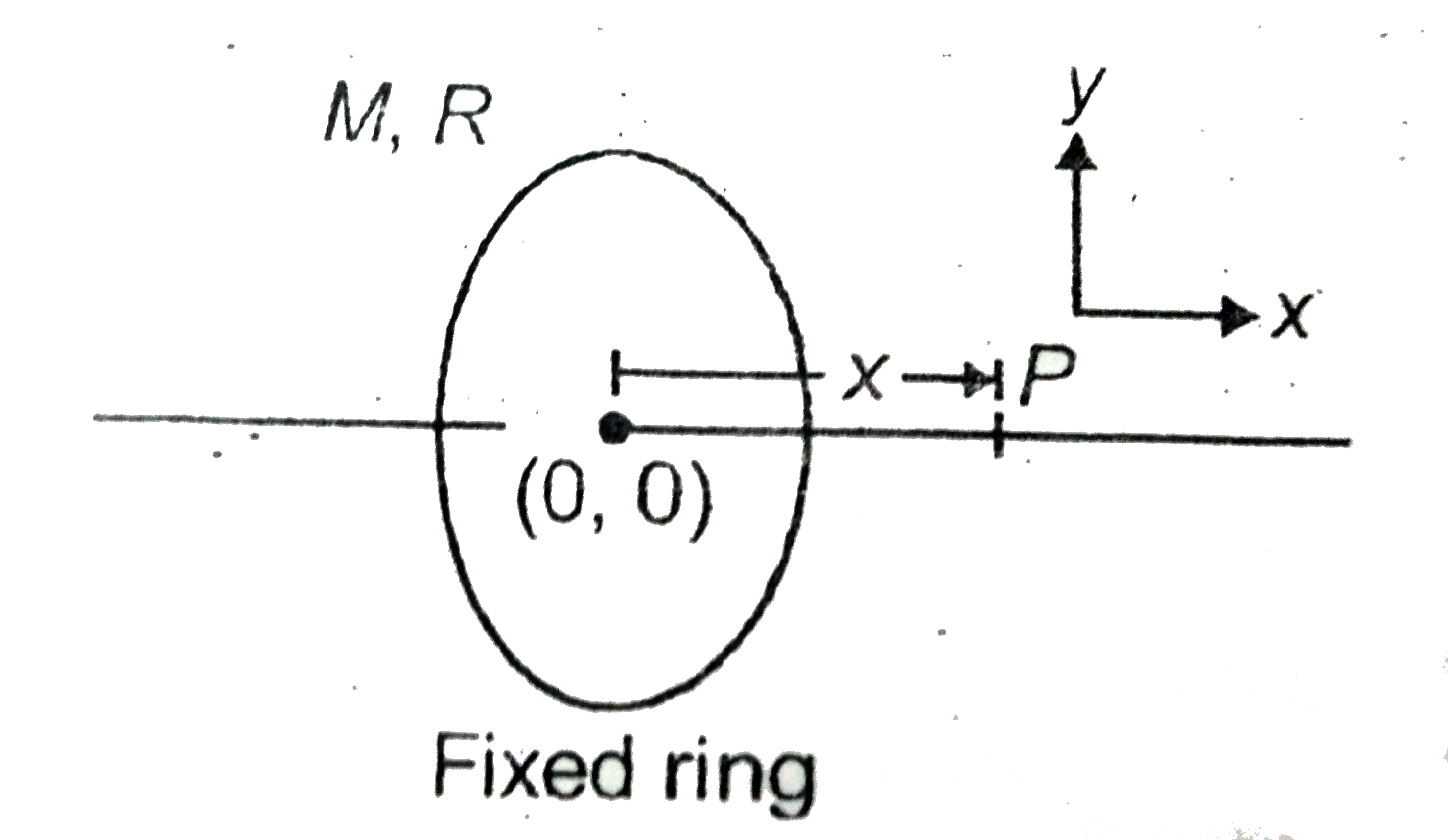
If the particle (mass m) is released from rest from a point distant x=R√3, then it will pass through the centre of ring with speedView SolutionA point P(R√3,0,0) lies on the axis of a ring of mass M and radius R. The ring is located in yx-plane with its centre at origin O. A small particle of mass m starts from P and reaches O under gravitational attraction only. Its speed at O will be
View SolutionTwo equal negative charges −q are fixed at points (0,−a) and (0,a) on y-axis. A poistive charge Q is released from rest at point (2a,0) on the x-axis. The charge Q will
View SolutionA circular ring carries a uniformly distributed positive charge and lies in the xy plane with center at the origin of the cooredinate system. If at a point (0,0,z) the electric field is E, then which of the following graphs is correct?
View SolutionA magnetic field B is confined to a region r≤ a and points out of the paper (the z-axis), r = 0 being the centre of the cicular region. A charged ring (charge = Q) of radius b,bgt a and mass m lie in the x-y plane with its centre at origin. The ring is free to rotate and is at rest. The magnetic field is brougth to zero in time Δt. Find the angular velocity omega or the ring after the field vanishes.
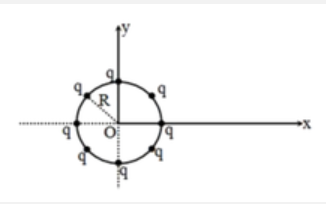
View SolutionEight charges each of value q are placed on a ring of radius R placed in x - y plane with origin at centre . A - q charge having mass m is projected from z=∞ towards the centre of the ring with velocity v . The velocity of - q when it reaches the centre of ring is (neglect gravity)
 View Solution
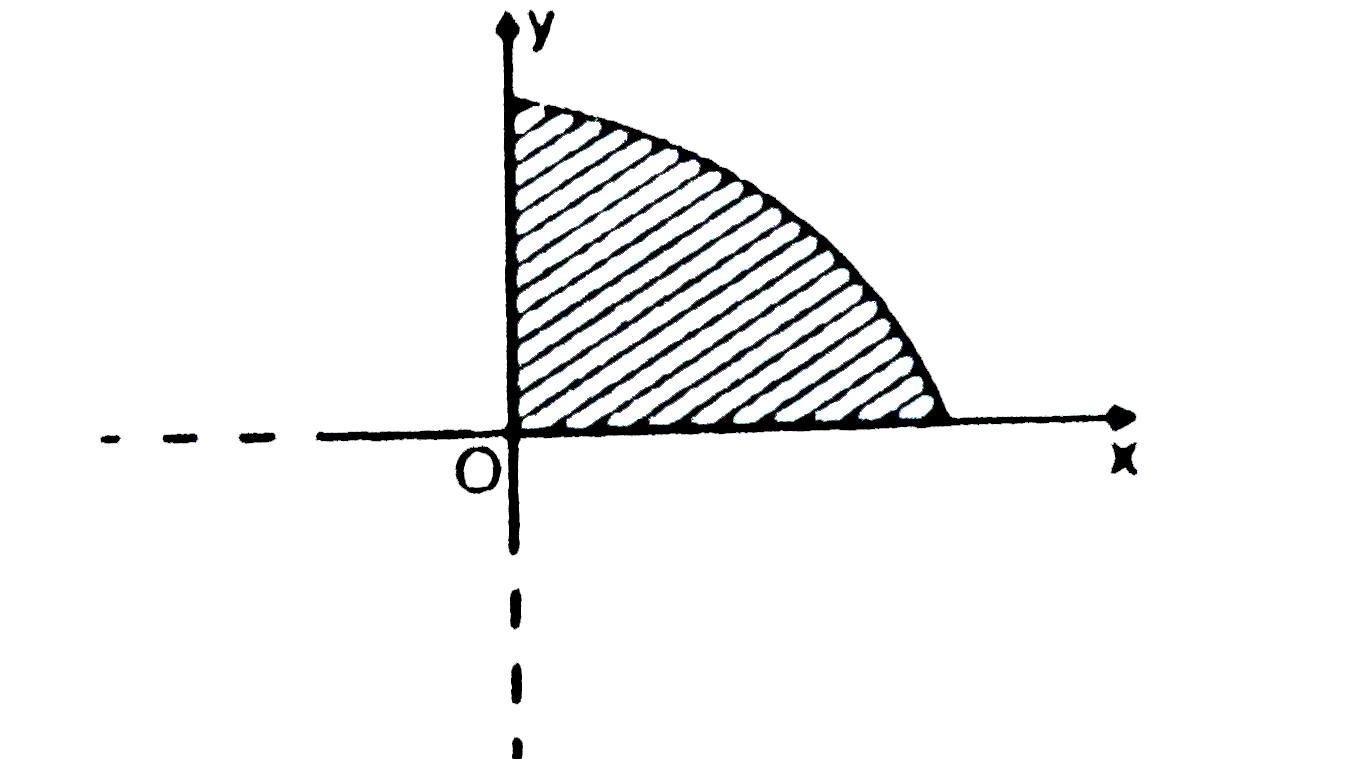
View SolutionA uniform surface charge of density σ is given to a quarter of a disc extending upto infinity in the first quadrant of x-y plane. The centre of the disc is at the origin O. Find the z-component of the electric field at the point (0,0,z) and the potential difference between the points (0,0,d) & (0,0,2d).
 View Solution
View Solution
