A positon dependent force ,F=8−4x+3x2N acts on a small body of mass 2 kg and displaces it from x=0 to x=5 m. The work done in joule is
35
70
115
270
The correct Answer is:C
To find the work done by the position-dependent force F=8−4x+3x2 on a small body of mass 2 kg as it displaces from x=0 to x=5 m, we will follow these steps:
Step 1: Understand the formula for work done
The work done W by a force F when moving an object through a displacement dx is given by the integral of the force with respect to displacement:
W=∫Fdx
Step 2: Set up the integral
Given the force F=8−4x+3x2, we need to integrate this force from x=0 to x=5:
W=∫50(8−4x+3x2)dx
Step 3: Perform the integration
We will integrate each term separately:
1. The integral of 8 with respect to x is 8x.
2. The integral of −4x is −2x2.
3. The integral of 3x2 is x3.
Thus, the integral becomes:
W=(8x−2x2+x3)50
Step 4: Evaluate the integral at the limits
Now we will evaluate the expression at the upper limit x=5 and the lower limit x=0:
1. At x=5:
W(5)=8(5)−2(52)+(53)=40−50+125=115
2. At x=0:
W(0)=8(0)−2(02)+(03)=0
Step 5: Calculate the work done
Now subtract the value at the lower limit from the value at the upper limit:
W=W(5)−W(0)=115−0=115 joules
Final Answer
The work done by the force is 115 joules.
The work done W by a force F when moving an object through a displacement dx is given by the integral of the force with respect to displacement:
W=∫Fdx
Given the force F=8−4x+3x2, we need to integrate this force from x=0 to x=5:
W=∫50(8−4x+3x2)dx
We will integrate each term separately:
1. The integral of 8 with respect to x is 8x.
2. The integral of −4x is −2x2.
3. The integral of 3x2 is x3.
W=(8x−2x2+x3)50
Now we will evaluate the expression at the upper limit x=5 and the lower limit x=0:
1. At x=5:
W(5)=8(5)−2(52)+(53)=40−50+125=115
2. At x=0:
W(0)=8(0)−2(02)+(03)=0
Now subtract the value at the lower limit from the value at the upper limit:
W=W(5)−W(0)=115−0=115 joules
The work done by the force is 115 joules.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - CHECK POINT 6.2
20 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - CHECK POINT 6.3
10 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions
11 Videos
Similar Questions
A position dependent force F=7−2x+3x2 acts on a small body of mass 2 kg and displaced it from x=0 to x=5m. Calculate the work done in joule.
View SolutionA force→F=(7−2x+3x2) N is applied on a 2 kg mass which displaces it from x = 0 to x = 5 m. Work done in joule is -
View SolutionConsider a variable force F=(3x+5)N acting on a body and if it is displaced from x=2m to x=4m, calculate the work done by this force.
View SolutionA position dependent force F acting on a particle and its force-position curve is shown in the figure. The work done by force from x=1 m to x=4 m is
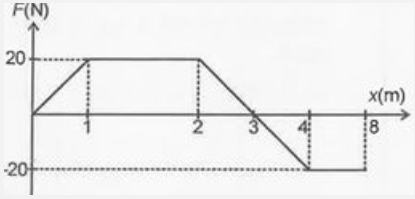
View SolutionFill in Blanks:
When a force of 2N causes a displacement of 0.5 m the work done is _____(1 pascal/1 joule)
View SolutionA position dependent force F ia acting on a particle and its force-position curve is shown in the figure. Work done on the particle, when its displacement is from 0 to 5 m is
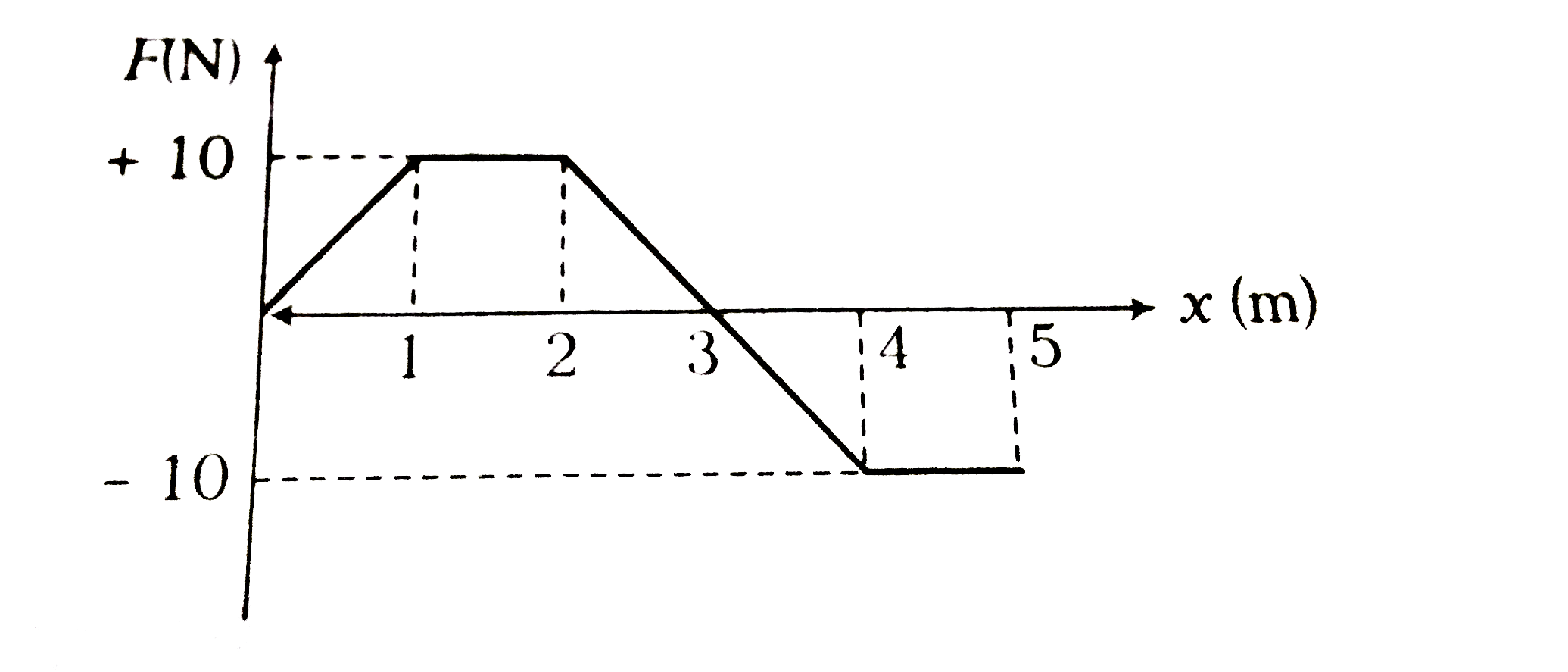
View SolutionUnder the action of a force F = Cx, the position of a body changes from 0 to x. The work done is
View SolutionA tangential force of F = 1.5 N acts on a particle of mass m = 2 kg revolving in a circular path of radius r = 3 m. What is the work done by the torque for a complete revolution of the particle ?
View SolutionA force given by the relation F=8t, acts on a body of mass 2kg, initialiy at rest. Find the work done by this force on the body during first 2 seconds of its motion.
View SolutionCertain force acting on a 20 kg mass changes its velocity from 5m/s→2m/s. calculate the work done by the force.
View Solution
