Under the action of a force F = Cx, the position of a body changes from 0 to x. The work done is
12Cx2
Cx2
Cx
12Cx
The correct Answer is:A
To solve the problem of finding the work done under the action of a force F=Cx as the position of a body changes from 0 to x, we can follow these steps:
Step 1: Understand the Work Done Formula
The work done W by a variable force can be calculated using the integral of the force over the distance moved. The formula is given by:
W=∫x2x1Fdx
where F is the force and x1 and x2 are the initial and final positions, respectively.
Step 2: Substitute the Force
In this case, the force is given as F=Cx. We need to substitute this into the work done formula:
W=∫x0Cxdx
Step 3: Factor Out the Constant
Since C is a constant, we can factor it out of the integral:
W=C∫x0xdx
Step 4: Perform the Integration
Now we need to integrate x:
∫xdx=x22
Thus, we can write:
W=C(x22)x0
Step 5: Evaluate the Integral
Now we evaluate the definite integral from 0 to x:
W=C(x22−022)=C(x22)
Step 6: Final Expression for Work Done
Therefore, the work done W is:
W=Cx22
Conclusion
The work done under the action of the force F=Cx as the position changes from 0 to x is:
W=Cx22
---
The work done W by a variable force can be calculated using the integral of the force over the distance moved. The formula is given by:
W=∫x2x1Fdx
where F is the force and x1 and x2 are the initial and final positions, respectively.
In this case, the force is given as F=Cx. We need to substitute this into the work done formula:
W=∫x0Cxdx
Since C is a constant, we can factor it out of the integral:
W=C∫x0xdx
Now we need to integrate x:
∫xdx=x22
Thus, we can write:
W=C(x22)x0
Now we evaluate the definite integral from 0 to x:
W=C(x22−022)=C(x22)
Therefore, the work done W is:
W=Cx22
The work done under the action of the force F=Cx as the position changes from 0 to x is:
W=Cx22
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MATCH THE COLUMNS7videos
WORK, ENERGY AND POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based2videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions11videos
WORK, POWER AND ENERGY
Similar Questions
A particle of mass 2 kg starts motion at time t = 0 under the action of variable force F = 4t (where F is in N and t is in s). The work done by this force in first two second is
View SolutionA 10−kg block moves in a straight line under the action of a force that varies with position as shown in figure. How much work does the force do as the block moves from origin to x=8m?
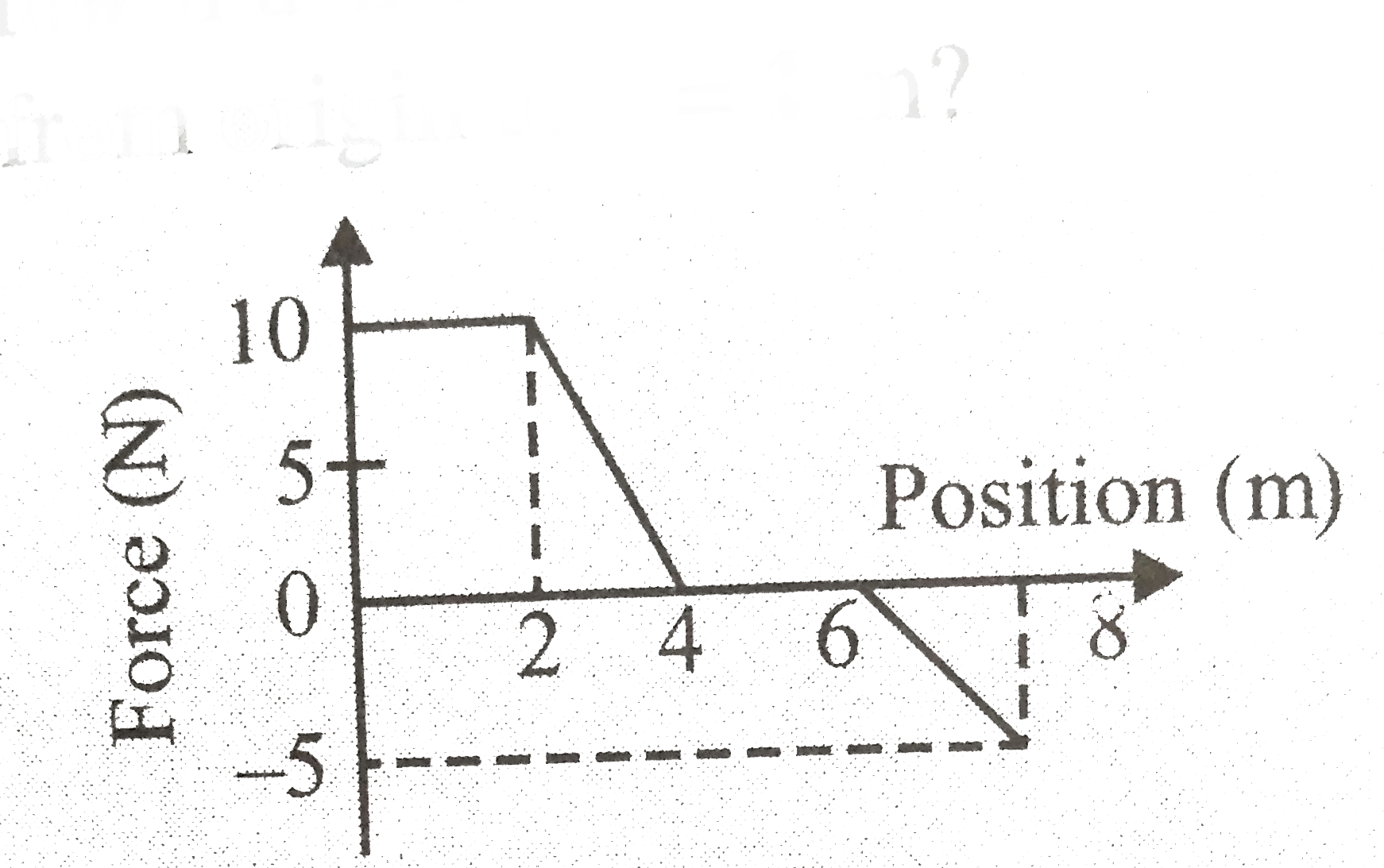 View Solution
View SolutionUnder the action of a force F=−kx3 , the motion of a particle is (k=a positive constant)
View SolutionA particale moves under the effect of a force F=Cx from x=0 to x=x1. The work down in the process is
View SolutionParticle moves from point A to point B along the line shown in figure under the action of force. evcF=−xˆi+yˆj. Determine the work done on the particle by →F in moving the particle from point A to point B.
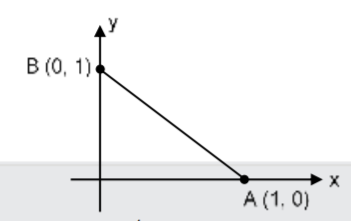 View Solution
View SolutionUnder the action of a force, a 2kg body moves such that its position x as a function of time is given by x=t33 where x is in meter and t in second. The work done by the force in the first two seconds is .
View SolutionUnder the action of a force, a 2kg body moves such that its position x as a function of time is given by x=t33 where x is in metre and t in second. The work done by the force in the first two seconds is .
View SolutionA particle is moving along x-axis under the action of a force, F which varies with its position (x) as F∝x−1/4. The variation of power due to this force with x is
View SolutionA particle moves from a point (2m,3m,0) to (3m,2m,0) under the action of force of magnitude 5N acting along the line y=x. The work done by the force on the particle during the displacement is
View SolutionA body moves from point A to B under the action of a force, varying in magnitude as shown in figure. Obtain the work done. Force is expressed in newton and displacement in meter.
 View Solution
View Solution

