A proton goes undflected in a crossed and magnetic field (the fields are perpendicular to each other) at a speed of The velocity is perpendicular to both the fields. When the electric field is switched off, the proton moves along a circle of radius 4.0 cm. Find the magnitudes of the electric and the magnetic fields. take the mass of the proton kg.
To solve the problem, we will follow these steps:
Step 1: Understand the Forces Acting on the Proton
When the proton is moving in crossed electric and magnetic fields, it experiences two forces:
- The electric force Fe=qE
- The magnetic force Fm=qvB
Since the proton goes undeflected, these two forces must be equal in magnitude:
Fe=Fm⟹qE=qvB
This simplifies to:
E=vB(Equation 1)
Step 2: Calculate the Magnetic Field B
When the electric field is switched off, the proton moves in a circular path due to the magnetic force. The radius R of the circular path is given by:
R=mvqB
Rearranging this equation gives us:
B=mvqR(Equation 2)
Step 3: Substitute Known Values into Equation 2
We know:
- Mass of the proton m=1.6×10−27 kg
- Velocity v=2.0×105 m/s
- Charge of the proton q=1.6×10−19 C
- Radius R=4.0 cm = 4.0×10−2 m
Now substituting these values into Equation 2:
B=(1.6×10−27kg)(2.0×105m/s)(1.6×10−19C)(4.0×10−2m)
Step 4: Calculate B
Calculating the numerator:
1.6×10−27×2.0×105=3.2×10−22
Calculating the denominator:
1.6×10−19×4.0×10−2=6.4×10−21
Now substituting these into the equation for B:
B=3.2×10−226.4×10−21=0.05T
Step 5: Calculate the Electric Field E
Now we can use Equation 1 to find E:
E=vB
Substituting the known values:
E=(2.0×105m/s)(0.05T)=1.0×104N/C
Final Results
- The magnitude of the magnetic field B=0.05T
- The magnitude of the electric field E=1.0×104N/C
When the proton is moving in crossed electric and magnetic fields, it experiences two forces:
- The electric force Fe=qE
- The magnetic force Fm=qvB
Fe=Fm⟹qE=qvB
This simplifies to:
E=vB(Equation 1)
When the electric field is switched off, the proton moves in a circular path due to the magnetic force. The radius R of the circular path is given by:
R=mvqB
Rearranging this equation gives us:
B=mvqR(Equation 2)
We know:
- Mass of the proton m=1.6×10−27 kg
- Velocity v=2.0×105 m/s
- Charge of the proton q=1.6×10−19 C
- Radius R=4.0 cm = 4.0×10−2 m
B=(1.6×10−27kg)(2.0×105m/s)(1.6×10−19C)(4.0×10−2m)
Calculating the numerator:
1.6×10−27×2.0×105=3.2×10−22
Calculating the denominator:
1.6×10−19×4.0×10−2=6.4×10−21
Now substituting these into the equation for B:
B=3.2×10−226.4×10−21=0.05T
Now we can use Equation 1 to find E:
E=vB
Substituting the known values:
E=(2.0×105m/s)(0.05T)=1.0×104N/C
- The magnitude of the magnetic field B=0.05T
- The magnitude of the electric field E=1.0×104N/C
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - QUESTIONS FOR SHORT ASNWER10videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective29videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective 110videos
MAGNETIC FIELD
- BOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer11videos
LIGHT WAVES
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer12videos
MAGNETIC FIELD DUE TO CURRENT
Similar Questions
A proton projected in a magnetic field of 0.020 T travels along a helical path of radius 5.0 cm and pitch 20 cm. Find the components of the velocity of the proton along and perpendicular to the magnetic field. Take the mass of the proton=1.6X10−27kg.
View SolutionA beam of electrons passes undeflected through uniformly perpendicular electric and magnetic fields. If the electric field is switched off, and the same magnetic field is maintained then the electrons move:
View SolutionIn a certain region of space electric field →E and magnetic field →B are perpendicular to each other and an electron enters in region perpendicular to the direction of →B and →E both and move underflected, then velocity of electron is
View Solution1 charge of 1C in a magnetic field of 0.5 Tesla with a velocity of 10m/sec Perpendicular to the field. Force experienced is
View SolutionThe momentum of α-particles moving in a circular path of radius 10 cm in a perpendicular magnetic field of 0.05 tesla will be :
View SolutionA proton is projected with a velocity of 3X106ms−1 perpendicular to a uniform magnetic field of 0.6 T. find the acceleration of the proton.
View SolutionIf the cyclotron oscillator frequency is 16 MHz, then what should be the operating magnetic field for accelerating the proton of mass 1.67×10−27kg?
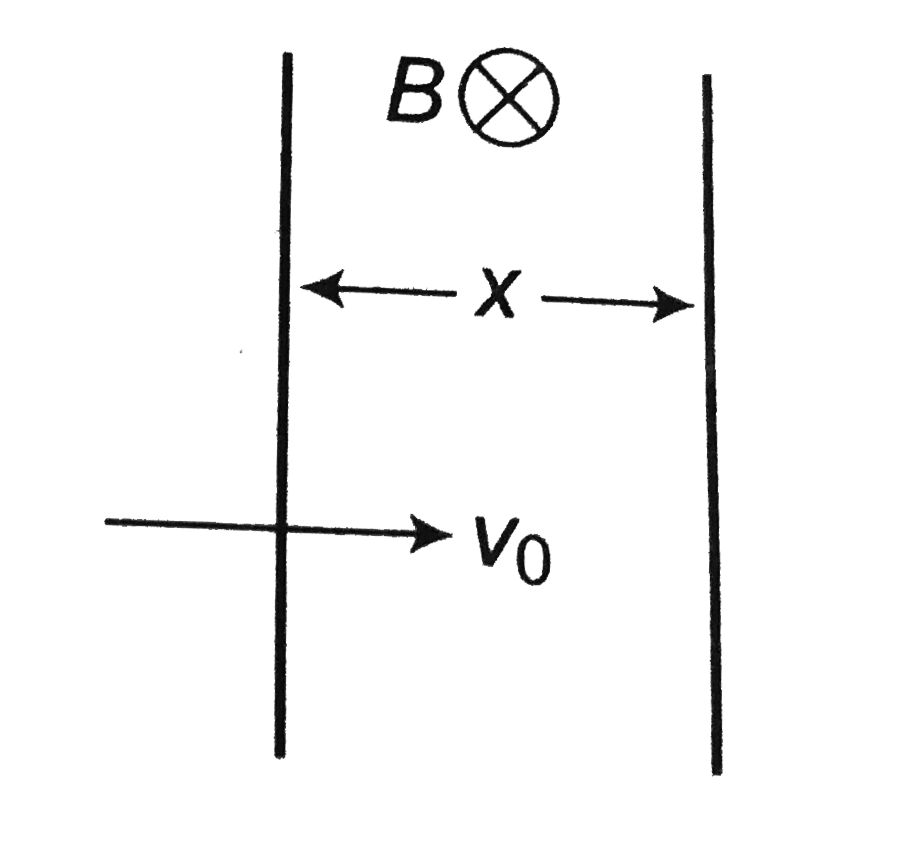
View SolutionA charged particle enters into a uniform magnetic field with velocity v0 perpendicular to it , the length of magnetic field is x=√32R, where R is the radius of the circular path of the particle in the field .The magnitude of charge in velocity of the particle when it comes out of the field is
 View Solution
View SolutionIn the figure shown a semicircular wire loop is placed in a uniform magnetic field B=1.0T. The plane of the loop is perpendicular to the magnetic field. Current i=2A flows in the loop in the directions shown. Find the magnitude of the magnetic force in both the cases a and b. The radius of the loop is 1.0 m
 View Solution
View SolutionIn the figure shown a semicircular wire loop is placed in a uniform magnetic field B=1.0T. The plane of the loop is perpendicular to the magnetic field. Current i=2A flows in the loop in the directions shown. Find the magnitude of the magnetic force in both the cases a and b. The radius of the loop is 1.0 m
 View Solution
View Solution

