A rectangular loop of sides 20 cm and 10 cm carries a current of 5.0 A. A uniform magnetic field of magnituded 0.20 T exists parallel ot the longer side of the loop (a) What is the force acting on the loop? (b) what is the torque acting on the loop?
To solve the problem, we will break it down into two parts: calculating the force acting on the rectangular loop and then calculating the torque acting on the loop.
Part (a): Force Acting on the Loop
1. Identify the dimensions and current:
- The rectangular loop has sides of 20 cm (0.20 m) and 10 cm (0.10 m).
- The current (I) flowing through the loop is 5.0 A.
- The magnetic field (B) is 0.20 T and is parallel to the longer side of the loop.
2. Determine the force on each side of the loop:
- The force on a straight conductor in a magnetic field is given by the formula:
F=BILsinθ
- Where:
- F is the force,
- B is the magnetic field,
- I is the current,
- L is the length of the conductor,
- θ is the angle between the magnetic field and the current.
3. Calculate the force on sides BC and DA:
- For side BC (length = 0.20 m):
- The angle θ between the magnetic field and the current is 180° (since they are parallel).
- Therefore, sin(180°)=0.
- Thus, the force on side BC:
FBC=B⋅I⋅LBC⋅sin(180°)=0
- For side DA (length = 0.20 m):
- The angle θ is also 0° (since they are parallel).
- Thus, the force on side DA:
FDA=B⋅I⋅LDA⋅sin(0°)=0
4. Calculate the force on sides AB and CD:
- For side AB (length = 0.10 m):
- The angle θ is 90°.
- Thus, the force on side AB:
FAB=B⋅I⋅LAB⋅sin(90°)=0.20⋅5.0⋅0.10⋅1=1.0N(inward)
- For side CD (length = 0.10 m):
- The angle θ is also 90°.
- Thus, the force on side CD:
FCD=B⋅I⋅LCD⋅sin(90°)=0.20⋅5.0⋅0.10⋅1=1.0N(outward)
5. Net force calculation:
- The net force F on the loop is the sum of the forces on all sides:
F=FAB+FBC+FCD+FDA=−1.0+0+1.0+0=0N
Part (b): Torque Acting on the Loop
1. Torque formula:
- The torque (τ) acting on a loop in a magnetic field is given by:
τ=N⋅B⋅I⋅A⋅sinα
- Where:
- N is the number of turns (1 for a single loop),
- A is the area of the loop,
- α is the angle between the normal to the loop and the magnetic field.
2. Calculate the area of the loop:
- The area A of the rectangular loop is:
A=length×width=0.20m×0.10m=0.02m2
3. Determine the angle α:
- Since the magnetic field is parallel to one side of the loop, the angle α between the normal to the plane of the loop and the magnetic field is 90°.
- Therefore, sin(90°)=1.
4. Calculate the torque:
- Substitute the values into the torque formula:
τ=1⋅0.20⋅5.0⋅0.02⋅1=0.02N m
Final Answers:
- (a) The net force acting on the loop is 0 N.
- (b) The torque acting on the loop is 0.02 N m.
- The rectangular loop has sides of 20 cm (0.20 m) and 10 cm (0.10 m).
- The current (I) flowing through the loop is 5.0 A.
- The magnetic field (B) is 0.20 T and is parallel to the longer side of the loop.
- The force on a straight conductor in a magnetic field is given by the formula:
F=BILsinθ
- Where:
- F is the force,
- B is the magnetic field,
- I is the current,
- L is the length of the conductor,
- θ is the angle between the magnetic field and the current.
- For side BC (length = 0.20 m):
- The angle θ between the magnetic field and the current is 180° (since they are parallel).
- Therefore, sin(180°)=0.
- Thus, the force on side BC:
FBC=B⋅I⋅LBC⋅sin(180°)=0
- The angle θ is also 0° (since they are parallel).
- Thus, the force on side DA:
FDA=B⋅I⋅LDA⋅sin(0°)=0
- For side AB (length = 0.10 m):
- The angle θ is 90°.
- Thus, the force on side AB:
FAB=B⋅I⋅LAB⋅sin(90°)=0.20⋅5.0⋅0.10⋅1=1.0N(inward)
- The angle θ is also 90°.
- Thus, the force on side CD:
FCD=B⋅I⋅LCD⋅sin(90°)=0.20⋅5.0⋅0.10⋅1=1.0N(outward)
- The net force F on the loop is the sum of the forces on all sides:
F=FAB+FBC+FCD+FDA=−1.0+0+1.0+0=0N
- The torque (τ) acting on a loop in a magnetic field is given by:
τ=N⋅B⋅I⋅A⋅sinα
- Where:
- N is the number of turns (1 for a single loop),
- A is the area of the loop,
- α is the angle between the normal to the loop and the magnetic field.
- The area A of the rectangular loop is:
A=length×width=0.20m×0.10m=0.02m2
- Since the magnetic field is parallel to one side of the loop, the angle α between the normal to the plane of the loop and the magnetic field is 90°.
- Therefore, sin(90°)=1.
- Substitute the values into the torque formula:
τ=1⋅0.20⋅5.0⋅0.02⋅1=0.02N m
- (a) The net force acting on the loop is 0 N.
- (b) The torque acting on the loop is 0.02 N m.
Topper's Solved these Questions
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - QUESTIONS FOR SHORT ASNWER
10 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective 1
10 Videos
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer
11 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer
12 Videos
Similar Questions
A square loop of sides 10cm carries a current of 10A.A uniform magnetic field of magnitude 0.20T exists parallel to one of the side of the loop.(a)What is the force acting on the loop? (b)What is the torque acting on the loop?
View SolutionA rectangular loop of dimensions (a×b) carries a current i. A uniform magnetic field →B=B0ˆi exists in space. Then :
View Solution
Knowledge Check
A conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of loop. What is the magnetic force acting on the loop?
AI r BB2πrIBCzeroDπrIB
A semicircular wire of radius 5.0 cm carries a current of 5.0 A. A magnetic field B of magnitude 0.50 T exists along the perpendicular to the plane of the wire. Find the magnitude of the magnetic force acting on the wire.
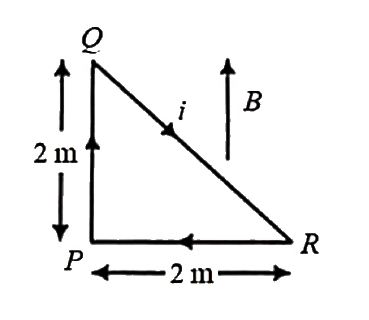
View SolutionA loop PQR carries a current i=2A as shown in the figure. A uniform magnetic field B = 2T exists in space parallel to the plane of the loop . The magnetic torque on the loop is
View SolutionA wire is bent in the form of an equilateral triangle PQR of side 10 cm and carries a current of 5.0 A. It is placed in a magnetic field B of magnitude 2.0 T directed perpendicularly to the plane of the loop. Find the forces on the three sides of the triangle.
View SolutionA current loop, carrying a current of 5.0 A, is in the shape of a right triangle with sides 30,40, and 50 cm. The loop is in a uniform magnetic field of magnitude 80 mT whose direction is parallel to the current in the 50 cm side of the loop. Find the magnitude of (a) the magnetic dipole moment of the loop and (b) the torque on the loop.
View SolutionTorque acting on a current loop in a uniform magnetic field is equal to
View SolutionA rectangular loop of sides 8 cm and 2 cm with a small cut is moving out of a region of uniform megnetic field of magnitude 0.3 tesla directed normal to the loop. What is the voltage developed acorss the cut if velocity of the loop is 1cms−1 in a direction normal to the (i) longer side (ii) shorter side of the loop ? For how long does the induced voltage last in each case?
View SolutionA rectangular loop of wire of size 4cm×10cm carries a steady current of 2A. A straight long wire carrying 5 A current is kept near the loop as shown. If the loop and the wire are coplanar, find
(i) the torque acting on the loop and
(ii) the magnitude and direction of the force on the loop due to the current carrying wire.

View Solution