A pulley fixed to the ceiling carried a thread with bodies of masses m1 and m2 attached to its ends. The mases of the pulley and the thread are negligible and friction is absent. Find the acceleration of the centre of mass of this system.
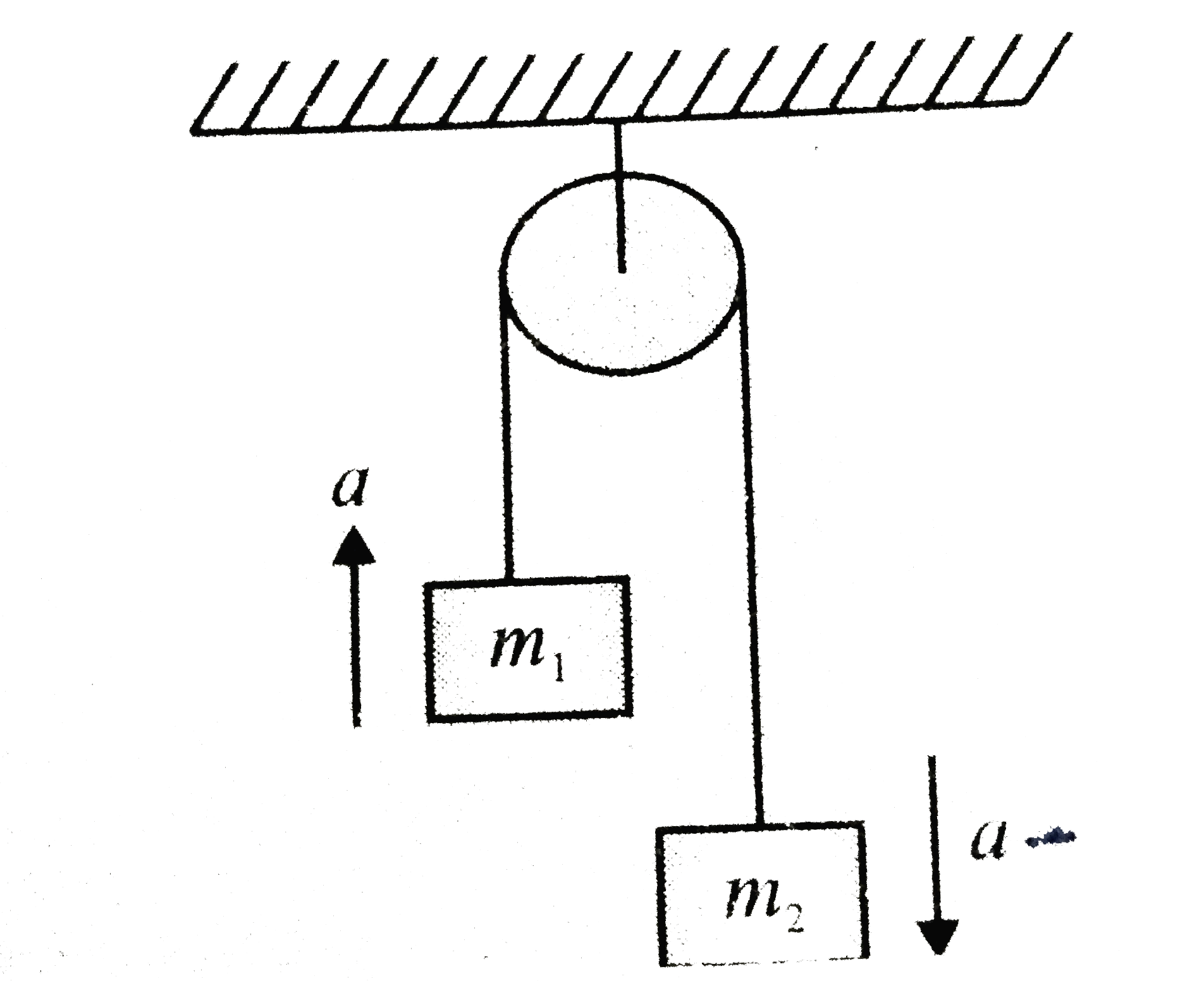
Let us assume that m2>m1. We can see that the masses have equal and opposite acceleration of the same magnitude.
a=m2−m1m2+m1g and tension in string is T=2m1m2gm2+m1
Taking downward direction as positive a1=−,a2=+a
aCM=m1a1+m2a2m1+m2=(m2−m1)am2+m1
substituting for the value of a we have
aCM=(m2−m1m2+m1)2g
Alternative method:
aCM=Fextm1+m2=(m1g+m2g)−2Tm1+m2=g−2Tm1+m2
=g−4m1m2g(m2+m1)2=(m2−m1m2+m1)2g (downwards)
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Solved Examples
13 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.1
20 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A pulley fixed to the ceiling carries a string with blocks of mass m and 3m attached to its ends. The masses of string and pulley are negligible .When the system is released, its center of mass moves with what acceleration
View SolutionTwo bodies with masses m1 and m2(m1>m2) are joined by a string passing over fixed pulley. Assume masses of the pulley and thread negligible. Then the acceleration of the centre of mass of the system (m1+m2) is
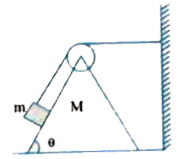
View SolutionA block of mass m is arranged on the wedge as shown in figure . The wedge angle is θ. If the masses of pulley and thread and negligible and friction is absent , find the acceleration of the wedge
View SolutionTwo blocks of masses 6kg and 4kg are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be
View SolutionA pulley fixed to the ceiling of an elevator car carries a thread whose ends are attached to the masses m1andm2. The car starts going up with an acceleration a0. Assuming the masses of the pulley and the thread as well as the friction to be negligible, find:
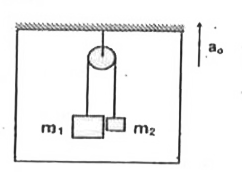
(a) the acceleration of the load m1 relative to the elevator shaft and relative to the car
(b) the force exerted by the pulley on the ceiling of the car. Given m1>m2.
View SolutionA rope thrown over a pulley has a on one of its ends and a counterbalancing mass M on its other end. The man whose mass is m, climbs upwards by →△r relative to the ladder and then stops. Ignoring masses of the pulley and the rope, as well as the friction the pulley axis, find the displacement of the centre of mass of this system.
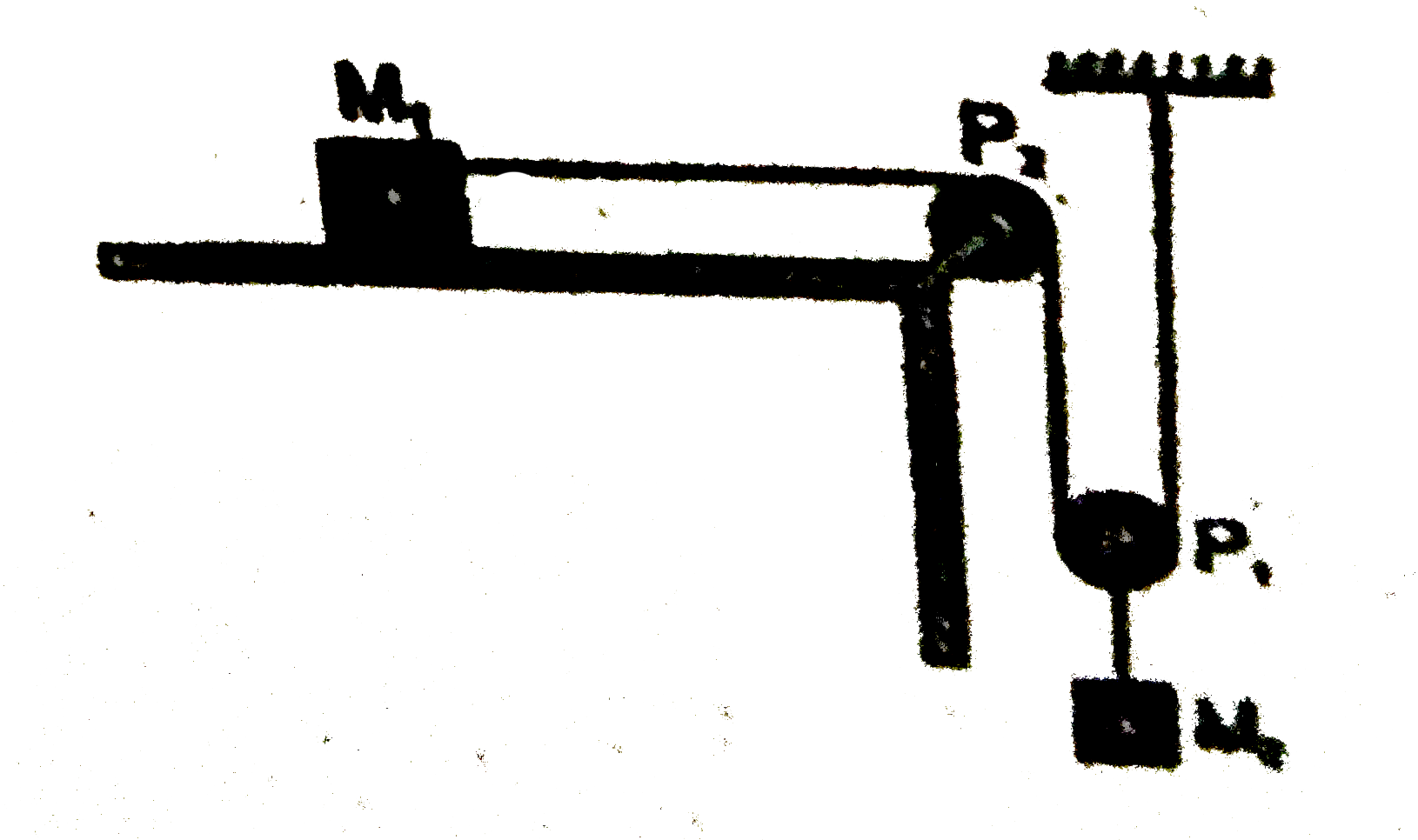
View SolutionBlocks of mass M1 and M2 are connected by a cord which passes over the pulleys P1 and P2 as shown in the figure. If there is no friction, the acceleration of the block of mass M2 will be
View SolutionIn the arrangement shown in figure the masses of the wedge M and the body m are known. The appreciable friction exists only between the wedge and the body m, the friction coefficient being equal to k. The masses of the pulley and the thread are negligible. Find the acceleration of the body m relative to the horizontal surface on which the wedge slides.

View Solution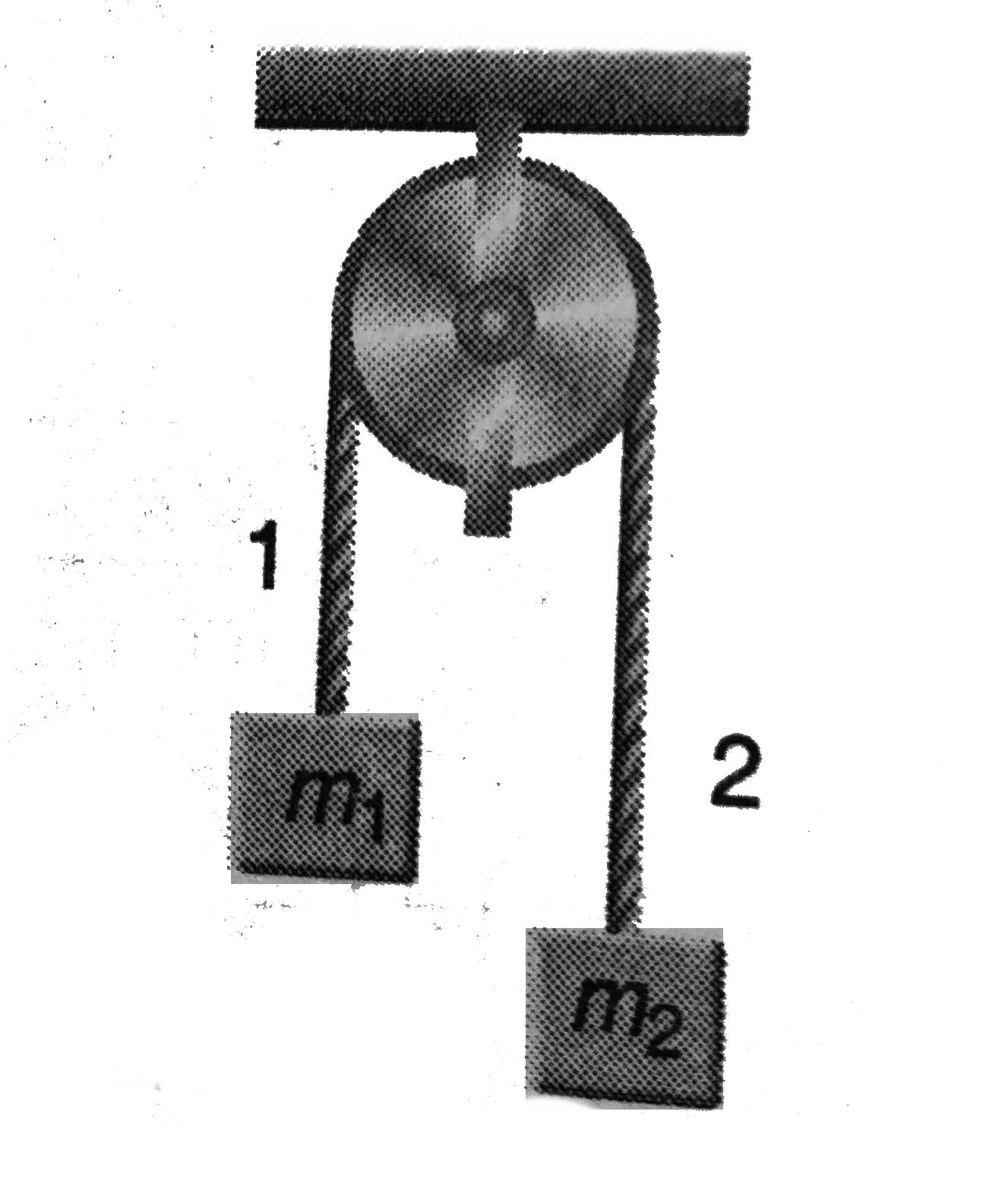
In the arrangement shown in figure the mass of the uniform solid cylindrical pulley of radius R is equal to m and the masses of two bodies are equal to m1 and m2. The thread slipping and the friction in the axle of the pulley are supposed to be absent. Find the angular acceleration of the cylinder and the ratio of tensions T1T2 of the vertical sections of the thread in the process of motion.
View SolutionA rope thrown over a pulley has a ladder with a man of mass m on one of its ends and a counter balancing mass M on its other end. The man climbs with a velocity vr relative to ladder. Ignoring the masses of the pulley and the rope as well as the friction on the pulley axis, the velocity of the centre of mass of this system is:
View Solution
