A racing car travels on a track (without banking) . is a circular arc of radius and are straight paths of length and is a circular arc of radius . The co-efficient of friction on the road is . the maximum speed of the car is . Find the minimum time for completing one round.
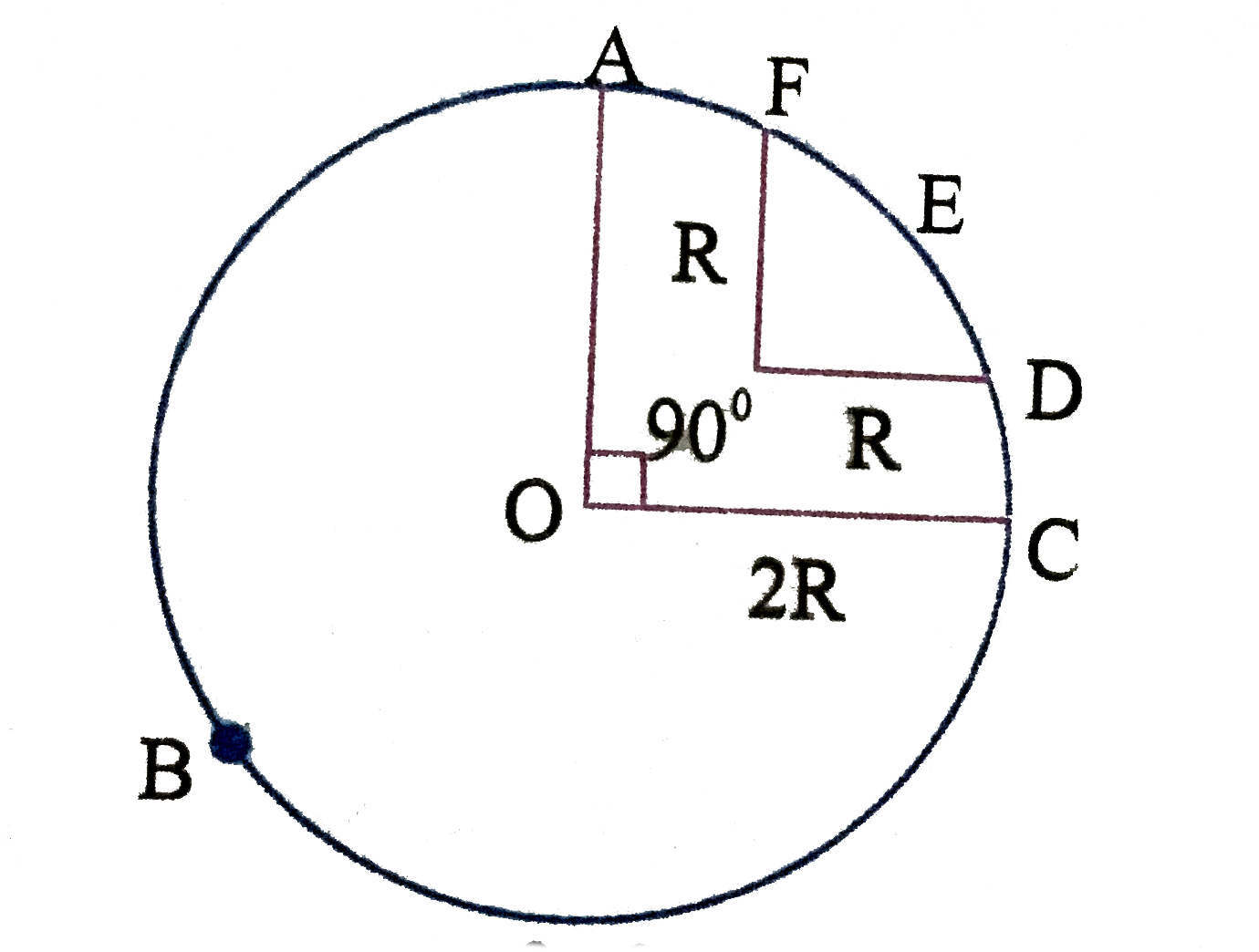 .
.
Balancing frictional force for centripetal force
where N is normal reaction
(where r is radius of the circular track)
For path ABC Path length =
=
= m/s
For path DEF Path length =
m/s
For paths CD and FA
Path length = R + R = 2R = 200 m
s.
Total time for completing one round
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Short answer type questions
6 Videos
- KINETIC THEORYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Multiple Choice Questions (MCQs)
31 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Long Answer Type Questions
3 Videos
Similar Questions
A car is taking turn on a circular path of radius R. If the coefficient of friction between the tyres and road is μ, the maximum velocity for no slipping is
View SolutionA car has to take a safe circular turn on horizontal flat rough road of radius 200 m. If the coefficient of friction between the tyres and road is 0.1 ,then maximum speed of car would be(All are in SI units)
View SolutionA car has to move on a level turn of radius 45 m. If the coefficient of static friction between the tyre and the road is μs=2.0, find the maximum speed the car can take without skidding.
View SolutionA car is moving on a horizontal circular track of radius 0.2 km with a constant speed. If coefficient of friction between tyres of car and road is 0.45, then maximum speed of car may be [Take g=10m/s2]
View SolutionA car of mass m is moving on a level circular track of radius R if μs represents the static friction between the road and tyres of the car, the maximum speed of the car in circular motion is given by.
View SolutionA car is moving on a horizontal circular road of radius 0.1 km with constant speed. If coefficient of friction between tyres of car and road is 0.4, then speed of car may be (g=10m/s2)
View SolutionA car turns a corner on a slippery road at a constant speed of 10 m /s . If the coefficient of friction is 0.5, the minimum radius of the arc in meter in which the car turns is
View SolutionA car goes on a horizontal circular road of radius R. The speed of car is increasing at constant rate a m/s2. If the friction coefficient between the road and the tyre is μ, then the limiting speed of car is
View SolutionWhat will be maximum speed of a car on a curved road of radius 30 m , If the coefficient of friction between the tyres and the road is 0.4?
(g=9.8m/s2)
View SolutionA car is moving on a circular level road of curvature 300m . If the coefficient of friction is 0.3 and acceleration due to gravity is 10m/s2 , the maximum speed of the car be a) 90 km/h b) 81 km/h c) 108 km/h d) 162 km/h
View Solution
