A ray of light is incident at an angle α on the boundary separating two transparant media. It transmited in other medium. If the angle incidence is increased very slightly, the ray gets reflected in the same medium. The different between angles of deviation in the two cases will close to
2α
90∘−α
180∘−α
180∘−α
The correct Answer is:B
To solve the problem, we need to analyze the situation of light rays incident at an angle α on the boundary of two transparent media and how the deviation changes when the angle of incidence is slightly increased.
1. Understanding the Critical Angle:
- When a ray of light is incident at an angle α and it transmits into another medium, we can infer that α is the critical angle. This means that the angle of refraction is 90∘ in the second medium.
2. Calculating Deviation for the First Case:
- When the light ray is incident at the critical angle α, the angle of deviation (δ1) can be calculated as:
δ1=90∘−α
- This is because the ray refracts at 90∘ to the normal.
3. Increasing the Angle of Incidence:
- If we increase the angle of incidence slightly beyond the critical angle, the ray will no longer transmit into the second medium but will instead reflect back into the first medium.
4. Calculating Deviation for the Second Case:
- In this case, the angle of incidence becomes slightly greater than α. Let's denote this new angle as α+ϵ (where ϵ is a very small angle).
- The angle of reflection will also be α+ϵ.
- The angle of deviation (δ2) for this case can be calculated as:
δ2=180∘−2(α+ϵ)
- Simplifying this gives:
δ2=180∘−2α−2ϵ
5. Finding the Difference in Angles of Deviation:
- Now, we can find the difference in the angles of deviation between the two cases:
Δδ=δ2−δ1
- Substituting the values we calculated:
Δδ=(180∘−2α−2ϵ)−(90∘−α)
- Simplifying this expression:
Δδ=180∘−2α−2ϵ−90∘+α
Δδ=90∘−α−2ϵ
6. Conclusion:
- As ϵ is very small, we can approximate:
Δδ≈90∘−α
- Thus, the difference between the angles of deviation in the two cases is approximately 90∘−α.
Final Answer:
The difference between the angles of deviation in the two cases will be close to 90∘−α.
- When a ray of light is incident at an angle α and it transmits into another medium, we can infer that α is the critical angle. This means that the angle of refraction is 90∘ in the second medium.
- When the light ray is incident at the critical angle α, the angle of deviation (δ1) can be calculated as:
δ1=90∘−α
- This is because the ray refracts at 90∘ to the normal.
- If we increase the angle of incidence slightly beyond the critical angle, the ray will no longer transmit into the second medium but will instead reflect back into the first medium.
- In this case, the angle of incidence becomes slightly greater than α. Let's denote this new angle as α+ϵ (where ϵ is a very small angle).
- The angle of reflection will also be α+ϵ.
- The angle of deviation (δ2) for this case can be calculated as:
δ2=180∘−2(α+ϵ)
- Simplifying this gives:
δ2=180∘−2α−2ϵ
- Now, we can find the difference in the angles of deviation between the two cases:
Δδ=δ2−δ1
- Substituting the values we calculated:
Δδ=(180∘−2α−2ϵ)−(90∘−α)
- Simplifying this expression:
Δδ=180∘−2α−2ϵ−90∘+α
Δδ=90∘−α−2ϵ
- As ϵ is very small, we can approximate:
Δδ≈90∘−α
- Thus, the difference between the angles of deviation in the two cases is approximately 90∘−α.
The difference between the angles of deviation in the two cases will be close to 90∘−α.
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - A. Only one option is correct (JEE Advance)
73 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - B. More than one option is correct
20 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
Similar Questions
A ray of light is incident as a normal ray on the surface of separation of two different mediums. What is the value of the angle of incidence in this case ?
View SolutionA light ray is incident fromt a denser medium on the boundary separating it from a rarer medium at an angle of incidence equal to the critical angle. What is the angle of refraction for the ray ?
View Solution
Knowledge Check
A light ray does not bend at the boundary in passing from one medium to the other medium if the angle of incidence is :
A0∘B45∘C60∘D90∘
A ray of light incident at the pole at angle 25∘ will be reflected at an angle 25∘
View SolutionLight from a denser medium 1 passes to a rarer medium 2. When the angle of incidence is θ the partially reflected and refracted rays are mutually perpendicular. The critical angle will be

View SolutionA ray of light is incident on the surface of seperation of a medium at an angle 45∘ and is refracted in the medium at an angle 30∘. What will be the velocity of light in the medium?
View SolutionA ray of monochromatic light is incident on the plane surface of separation between two media x and y with angle of incidence i in the medium x and angle of refraction r in the medium y. The graph shows the relation between sin i and sin r.

View SolutionA ray of light-is incident on glass at the polarising angle ip. Find the angle between the reflected and refracted rays.
View SolutionIn the figure given the angle between incident ray and the reflected ray is 70∘
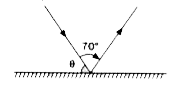
Find the angle of reflection.
View SolutionA ray of light incident at an angle of incidence 48∘ on a prism of refracting angle 60∘ suffers minimum deviation. Calculate the angle of minimum deviation.
View Solution
