A ray of light is incident on the surface of seperation of a medium at an angle 45∘ and is refracted in the medium at an angle 30∘. What will be the velocity of light in the medium?
1.96×108 m/s
2.12×108 m/s
2.65×108 m/s
1.24×108 m/s
The correct Answer is:B
To solve the problem step by step, we will use Snell's Law and the relationship between the speed of light in different media.
Step 1: Identify the given values
- Angle of incidence (I) = 45°
- Angle of refraction (R) = 30°
- Speed of light in vacuum (C) = 3 × 10^8 m/s
Step 2: Use Snell's Law
Snell's Law states that:
μ=sinIsinR
where μ is the refractive index of the medium.
Step 3: Calculate the refractive index
Substituting the values into Snell's Law:
μ=sin(45°)sin(30°)
Using the known values:
- sin(45°)=1√2
- sin(30°)=12
Now substituting these values:
μ=1√212=2√2=√2
Step 4: Relate the refractive index to the speed of light
The refractive index is also related to the speed of light in vacuum (C) and the speed of light in the medium (v) by the formula:
μ=Cv
Step 5: Rearranging to find the speed of light in the medium
Rearranging the equation gives:
v=Cμ
Step 6: Substitute the values
Now substituting the values of C and μ:
v=3×108 m/s√2
Step 7: Calculate the value of v
Calculating v:
v=3×108×1√2
v≈3×108×0.7071
v≈2.1213×108 m/s
Final Answer
Thus, the velocity of light in the medium is approximately:
v≈2.12×108 m/s
- Angle of incidence (I) = 45°
- Angle of refraction (R) = 30°
- Speed of light in vacuum (C) = 3 × 10^8 m/s
Snell's Law states that:
μ=sinIsinR
where μ is the refractive index of the medium.
Substituting the values into Snell's Law:
μ=sin(45°)sin(30°)
- sin(45°)=1√2
- sin(30°)=12
μ=1√212=2√2=√2
The refractive index is also related to the speed of light in vacuum (C) and the speed of light in the medium (v) by the formula:
μ=Cv
Rearranging the equation gives:
v=Cμ
Now substituting the values of C and μ:
v=3×108 m/s√2
Calculating v:
v=3×108×1√2
v≈3×108×0.7071
v≈2.1213×108 m/s
Thus, the velocity of light in the medium is approximately:
v≈2.12×108 m/s
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - medical entrance special format question
23 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Medical entrance gallary
76 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.7
10 Videos
- NUCLEIBOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - C MADICAL ENTRANCES GALLERY
46 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
Similar Questions
When light is refracted into a medium
View SolutionWhen light is refracted into a medium
View SolutionA ray of light falls on the surface of a spherical glass paper weight making an angle α with the normal and is refracted in the medium at an angle β. The angle of deviation of the emergent ray from the direction of the incident ray is :
View SolutionA ray of light falls on the surface of a spherical glass paper weight making an angle α with the normal and is refracted in the medium at an angle β. The angle of deviation of the emergent ray from the direction of the incident ray is :
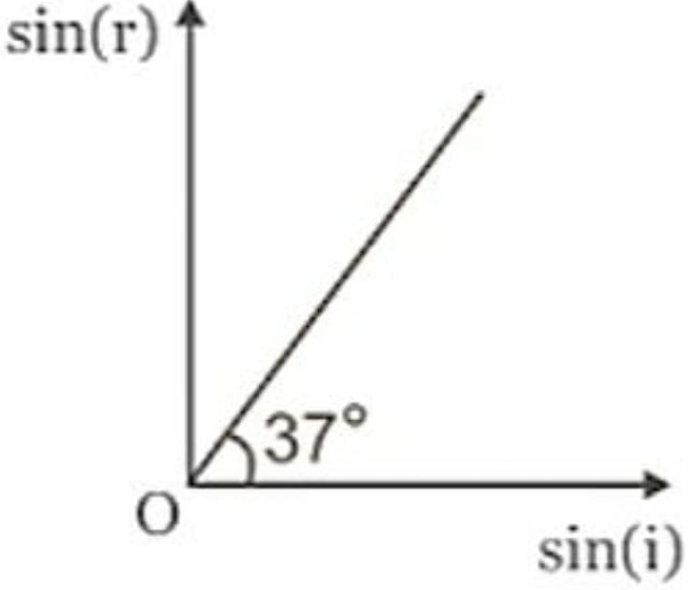
View SolutionA ray of monochromatic light is incident on the plane surface of separation between two media x and y with angle of incidence i in the medium x and angle of refraction r in the medium y. The graph shows the relation between sin i and sin r.

View SolutionIf the critical angle for total internal reflection, from a medium to vacuum is 30∘, then velocity of light in the medium is
View SolutionA ray of light is incident on a transparent medium at polarizing angle. What is the angle between the reflected ray and the refracted ray .
View SolutionA ray of light is incident as a normal ray on the surface of separation of two different mediums. What is the value of the angle of incidence in this case ?
View SolutionWhen unpolarised light is incident on the interface separating the rarer medium and the denser medium, Brewster angle is found to be 60∘ . Determine the refractive index of the denser medium.
View SolutionA ray of light travelling in medium. A is incident on the plane interface of two medium W and B and gets refracted into the medium B. The angle of incidence is I and that of refraction is r. The graph between sin(i) and sin(r) is a shown in the diagram . The correct Statement among the following is
View Solution
