A ray of light is incident on a horizontal plane mirror at an angle of incidence 30∘. By what angle should the mirror be rotated so that the reflected ray becomes horizontal?
To solve the problem, we need to determine the angle by which the mirror should be rotated so that the reflected ray becomes horizontal after the initial incident ray strikes the mirror at an angle of incidence of 30 degrees. Here’s a step-by-step solution:
Step 1: Understand the Law of Reflection
According to the law of reflection, the angle of incidence (i) is equal to the angle of reflection (r).
Hint: Remember that the angle of incidence is measured from the normal to the surface of the mirror.
Step 2: Identify the Given Values
From the problem, we know:
- Angle of incidence (i) = 30 degrees
- Therefore, angle of reflection (r) = 30 degrees (by the law of reflection).
Hint: Make sure to visualize the angles with respect to the normal line to the mirror.
Step 3: Determine the Angle with the Vertical
Since the mirror is horizontal, the angle of the reflected ray with the vertical can be calculated as:
θ=90∘−r
Substituting the value of r:
θ=90∘−30∘=60∘
Hint: The angle with the vertical is complementary to the angle of reflection.
Step 4: Determine the Required Rotation of the Mirror
To make the reflected ray horizontal, we need it to be at an angle of 0 degrees with respect to the horizontal line. This means that the angle with the vertical should be 90 degrees.
To achieve this, we need to rotate the mirror such that the angle of reflection changes from 30 degrees to 90 degrees. The change in angle required is:
Change in angle=90∘−30∘=60∘
Hint: Think about how rotating the mirror affects the angles of incidence and reflection.
Step 5: Conclusion
Thus, the mirror should be rotated by 30 degrees to achieve the desired condition where the reflected ray becomes horizontal.
Final Answer: The mirror should be rotated by 30 degrees.
According to the law of reflection, the angle of incidence (i) is equal to the angle of reflection (r).
From the problem, we know:
- Angle of incidence (i) = 30 degrees
- Therefore, angle of reflection (r) = 30 degrees (by the law of reflection).
Since the mirror is horizontal, the angle of the reflected ray with the vertical can be calculated as:
θ=90∘−r
Substituting the value of r:
θ=90∘−30∘=60∘
To make the reflected ray horizontal, we need it to be at an angle of 0 degrees with respect to the horizontal line. This means that the angle with the vertical should be 90 degrees.
Change in angle=90∘−30∘=60∘
Thus, the mirror should be rotated by 30 degrees to achieve the desired condition where the reflected ray becomes horizontal.
Topper's Solved these Questions
- RAY OPTICSBOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - PROBLEMS ( LEVEL-I)
57 Videos
- RAY OPTICSBOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - PROBLEMS ( LEVEL-II)
60 Videos
- RAY OPTICSBOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - EXERCISE (SHORT ANSWER QUESTIONS )
24 Videos
- PRACTICAL PHYSICSBOOK - AAKASH SERIESCHAPTER - PRACTICAL PHYSICSEXERCISE - LECTURE SHEET LEVEL-II (ADVANCED) Linked Comprehension Type Questions
4 Videos
- SEMICONDUCTOR DEVICESBOOK - AAKASH SERIESCHAPTER - SEMICONDUCTOR DEVICESEXERCISE - EXERCISE - III
3 Videos
Similar Questions
A ray of light is incident on a plane mirror at an angle of incidence of 30∘. The deviation produced by the mirror is
View SolutionA light ray strikes a horizontal plane mirror and gets deviated by π/3. By what angle should the mirror be tilted so that the reflected ray becomes vertical?
View SolutionA light ray is incident normally on a plane mirror.
What is the angle of incidence?
View SolutionA light ray is incident normally on a plane mirror.
What is its angle of incidence?
View SolutionA ray of light falls normally on a plane mirror. What is the angle of incidence ?
View Solutionrays of light strike a horizontal plane mirror at an angle of 45∘. At what angle should be a second plane mirror be placed in order that the reflected ray finally be reflected horizontally from the second mirror.
View SolutionA horizontal light ray passes through a prism (μ=1.5) of angle 4∘.Further, it is incident on a plane mirror M, that has been placed verticall. By what angle the mirror is rotated so that the ray after reflection becomes horizontal?
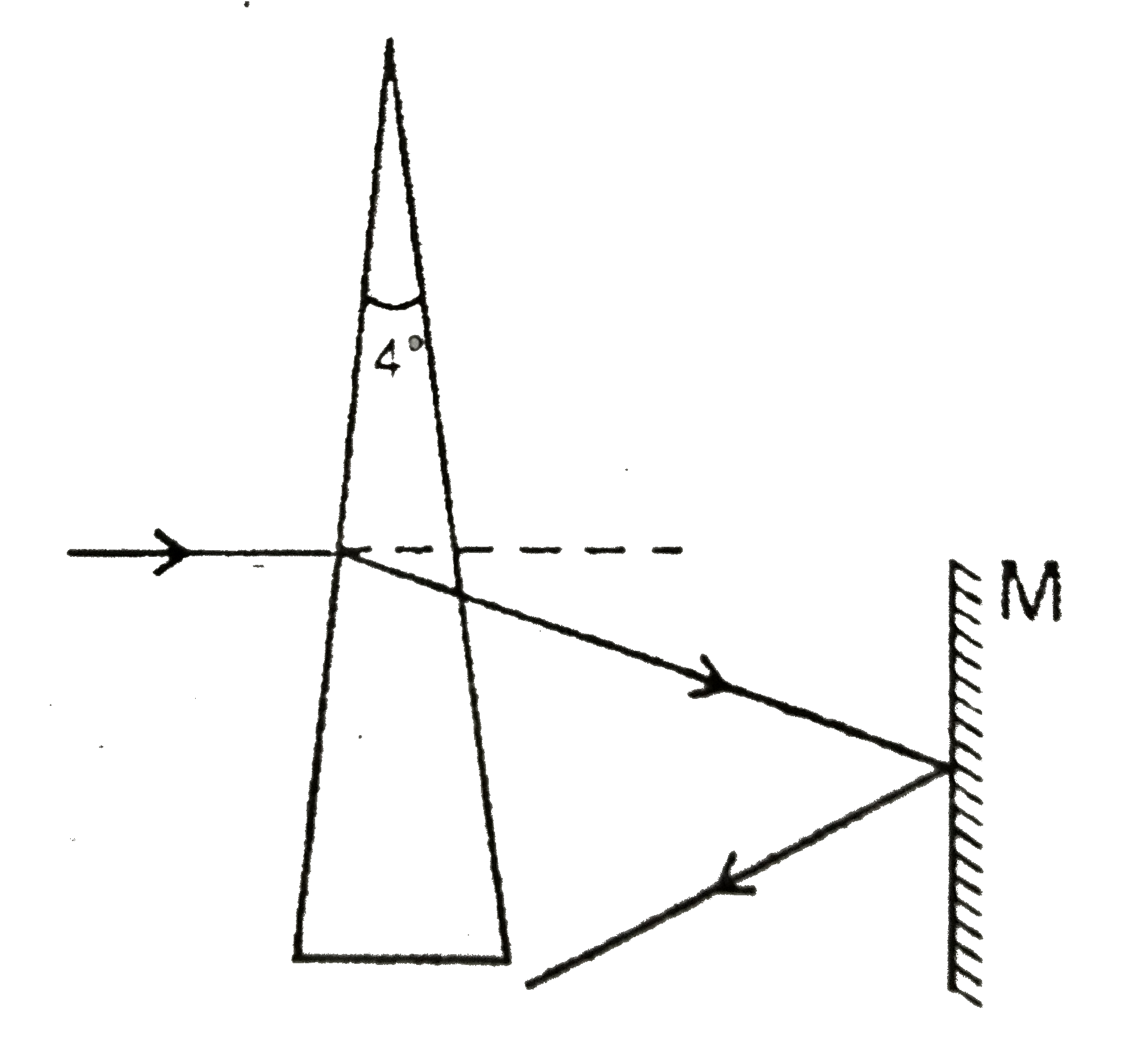
View Solutiona ray of light is incident on a plane miror at an angle of 30∘ in anti-clockwise direction. Find the angle and sense of rotation of the reflected ray.

View SolutionWhen a ray of light falls normally on a plane mirror. The angle of incidence will be
View SolutionWhen a ray of light strikes a plane mirror along the normal, the angle of incidence is :
View Solution
