A light ray strikes a horizontal plane mirror and gets deviated by π/3. By what angle should the mirror be tilted so that the reflected ray becomes vertical?
π/6
(π)/2
π3
(π)/4
The correct Answer is:A
To solve the problem, we need to determine the angle by which the mirror should be tilted so that the reflected ray becomes vertical after initially being deviated by π3.
1. Understand the Initial Setup:
- A light ray strikes a horizontal plane mirror and is deviated by an angle of π3 (or 60 degrees). This means that the angle of reflection is also π3 due to the law of reflection, which states that the angle of incidence is equal to the angle of reflection.
2. Determine the Angle of Incidence:
- Let the angle of incidence be i. According to the law of reflection:
i=π3
- The angle between the incident ray and the normal (which is vertical in this case) is:
Angle with normal=π2−i=π2−π3=π6
3. Determine the Required Angle for Vertical Reflection:
- For the reflected ray to become vertical, the angle of reflection must be 0 with respect to the vertical axis. This means that we need to adjust the angle of incidence such that the reflected ray is directed straight up.
4. Tilt the Mirror:
- If we tilt the mirror by an angle θ, the angle of incidence will change. The new angle of incidence will be:
i′=i+θ
- The new angle of reflection will also be equal to the new angle of incidence:
r′=i′=i+θ
- For the reflected ray to be vertical, we need:
r′=0⇒i+θ=0⇒θ=−i
- Since i=π3, we have:
θ=−π3
5. Calculate the Total Tilt:
- However, we are looking for the angle by which the mirror should be tilted to achieve this condition. Since the original angle of incidence was π3, we need to tilt the mirror by an angle that compensates for this deviation:
Tilt angle=π6
Final Answer:
The mirror should be tilted by π6 (or 30 degrees) so that the reflected ray becomes vertical.
- A light ray strikes a horizontal plane mirror and is deviated by an angle of π3 (or 60 degrees). This means that the angle of reflection is also π3 due to the law of reflection, which states that the angle of incidence is equal to the angle of reflection.
- Let the angle of incidence be i. According to the law of reflection:
i=π3
- The angle between the incident ray and the normal (which is vertical in this case) is:
Angle with normal=π2−i=π2−π3=π6
- For the reflected ray to become vertical, the angle of reflection must be 0 with respect to the vertical axis. This means that we need to adjust the angle of incidence such that the reflected ray is directed straight up.
- If we tilt the mirror by an angle θ, the angle of incidence will change. The new angle of incidence will be:
i′=i+θ
- The new angle of reflection will also be equal to the new angle of incidence:
r′=i′=i+θ
- For the reflected ray to be vertical, we need:
r′=0⇒i+θ=0⇒θ=−i
- Since i=π3, we have:
θ=−π3
- However, we are looking for the angle by which the mirror should be tilted to achieve this condition. Since the original angle of incidence was π3, we need to tilt the mirror by an angle that compensates for this deviation:
Tilt angle=π6
The mirror should be tilted by π6 (or 30 degrees) so that the reflected ray becomes vertical.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - PRACTICE SHEET (EXERCISE I LEVEL -II (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS)
7 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - PRACTICE SHEET (EXERCISE I LEVEL -II (ADVANCED) MORE THAN ONE CORRECT TYPE QUESTIONS)
2 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE III LEVEL -II (ADVAMCED) INTEGER TYPE QUESTIONS)
2 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
106 Videos
Similar Questions
rays of light strike a horizontal plane mirror at an angle of 45∘. At what angle should be a second plane mirror be placed in order that the reflected ray finally be reflected horizontally from the second mirror.
View SolutionA horizontal light ray passes through a prism (μ=1.5) of angle 4∘.Further, it is incident on a plane mirror M, that has been placed verticall. By what angle the mirror is rotated so that the ray after reflection becomes horizontal?
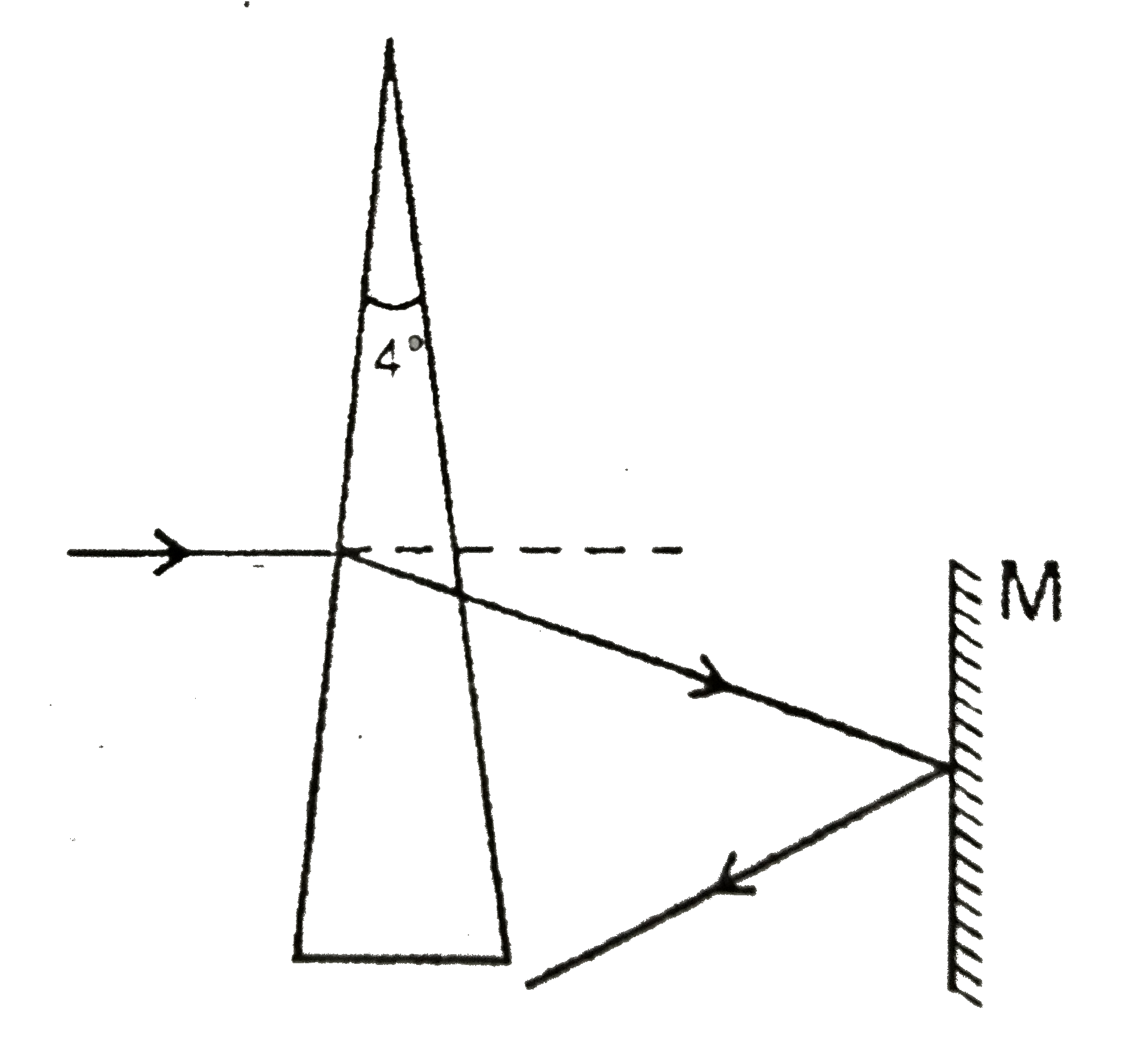
View SolutionA ray of light makes an angle of 10∘ with the horizontal and strikes a plane mirror which is inclined at an angle θ to the horizontal. The angle θ for which the reflected ray becomes vertical, is
View SolutionA horizontal ray of light passes through a prism of index 1.50 and apex angle 4∘ and then strikes a vertical mirror , as shown in the figure. Through what angle must the mirror be rotated if after reflection the ray is to be horizontal?
_E01_041_Q01.png)
View SolutionRays of light are incident on a plane mirror at 40∘. At what angle with the first should a second mirror be placed such that the rays emerge from the second mirror parallel to the first mirror.
View SolutionA light ray is incident on a plane mirror at an angle of 30∘ with horizontal. At what angle with horizontal must a plane mirror be placed in its path so that it becomes vertically upwards after reflection?
View SolutionTwo plane mirrors are arranged at right angles to each other as shown in figure.A ray of light is incident on the horizontal mirror at an angle θ. For what value of θthe ray emerges parallel to the incoming ray after reflection from the vertical mirror ?

View SolutionThe diagram below shows a light ray striking and reflecting from a plane mirror AO is the incident ray and OB the reflected ray. The angle between the incident ray and the reflected ray is 120∘.
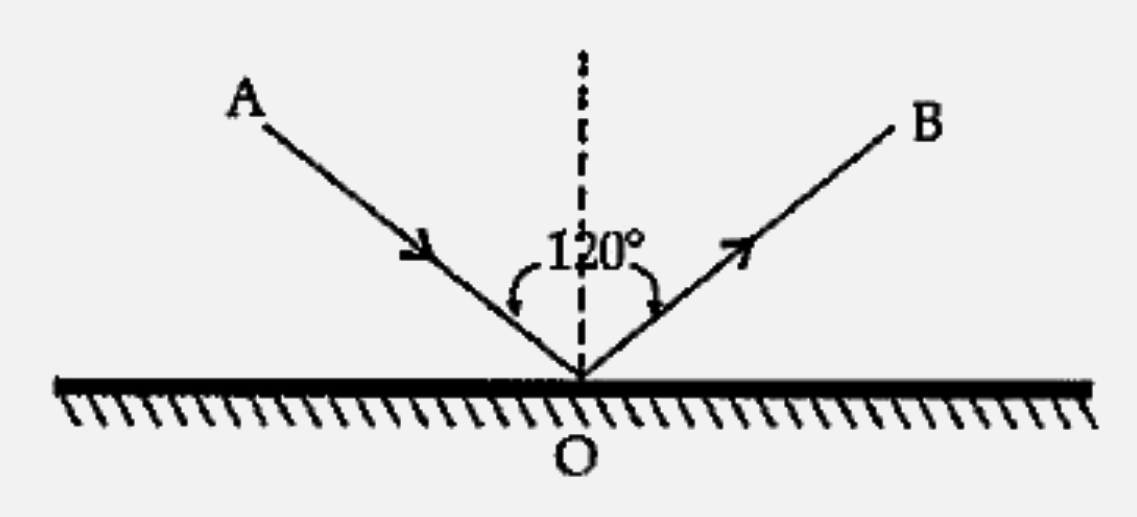
What is the value of the angle of reflection?
View SolutionThe diagram below shows a light ray striking and reflecting from a plane mirror AO is the incident ray and OB the reflected ray. The angle between the incident ray and the reflected ray is 120∘.

If the image of an object is formed 5 cm behind the mirror, what is the distance between the image and the object?
View SolutionThe diagram below shows a light ray striking and reflecting from a plane mirror AO is the incident ray and OB the reflected ray. The angle between the incident ray and the reflected ray is 120∘.

If two plane mirrors are used and kept facing parallel to each other, how many images are formed if the object is kept in between them?
View Solution
