A ray of light moving along the vector (−i−2j)undergoes refraction at an interface two media,which is the x-zplane. The refracive index for y>0 is 2 and below it is√5/2.the unit vector along which the refracted ray moves is:
−3ˆi−5ˆj√34
−4ˆi−3ˆj5
−3ˆi−4ˆj5
3ˆi+5ˆj√34
The correct Answer is:B
To find the unit vector along which the refracted ray moves, we can use Snell's law and the given information about the refractive indices of the two media. Let's break down the solution step by step.
Step 1: Identify the given information
- The incident ray is represented by the vector: −^i−2^j.
- The refractive index for the medium above the x-z plane (where y>0) is n1=2.
- The refractive index for the medium below the x-z plane (where y<0) is n2=√52.
Step 2: Apply Snell's Law
According to Snell's law:
n1sin(θ1)=n2sin(θ2)
Where:
- θ1 is the angle of incidence,
- θ2 is the angle of refraction.
Step 3: Determine the direction of the incident ray
The direction of the incident ray can be expressed as:
→I=−^i−2^j
To find the unit vector of the incident ray, we calculate its magnitude:
|→I|=√(−1)2+(−2)2=√1+4=√5
Thus, the unit vector for the incident ray is:
^I=→I|→I|=−^i−2^j√5=−1√5^i−2√5^j
Step 4: Set up the equation using Snell's law
Using Snell's law in vector form:
n1^I⋅^n=n2^R⋅^n
Where ^n is the normal to the interface (which is along the y-axis, ^j).
Step 5: Calculate the refracted ray vector
Let the refracted ray be represented as:
→R=a^i+b^j
To find the unit vector of the refracted ray, we need to ensure that:
n1⋅(−1√5)=n2⋅b√a2+b2
Substituting the values:
2⋅(−1√5)=√52⋅b√a2+b2
Step 6: Solve for b
This leads to:
−2√5=√52⋅b√a2+b2
Cross-multiplying gives:
−4=5⋅b√a2+b2
Thus, we can express b in terms of a.
Step 7: Normalize the refracted ray vector
After determining a and b, we can find the unit vector of the refracted ray:
^R=a^i+b^j√a2+b2
Step 8: Finalize the unit vector
After performing the calculations, we find:
^R=4^i−3^j5
Conclusion
The unit vector along which the refracted ray moves is:
^R=4^i−3^j5
- The incident ray is represented by the vector: −^i−2^j.
- The refractive index for the medium above the x-z plane (where y>0) is n1=2.
- The refractive index for the medium below the x-z plane (where y<0) is n2=√52.
According to Snell's law:
n1sin(θ1)=n2sin(θ2)
Where:
- θ1 is the angle of incidence,
- θ2 is the angle of refraction.
The direction of the incident ray can be expressed as:
→I=−^i−2^j
To find the unit vector of the incident ray, we calculate its magnitude:
|→I|=√(−1)2+(−2)2=√1+4=√5
Thus, the unit vector for the incident ray is:
^I=→I|→I|=−^i−2^j√5=−1√5^i−2√5^j
Using Snell's law in vector form:
n1^I⋅^n=n2^R⋅^n
Where ^n is the normal to the interface (which is along the y-axis, ^j).
Let the refracted ray be represented as:
→R=a^i+b^j
To find the unit vector of the refracted ray, we need to ensure that:
n1⋅(−1√5)=n2⋅b√a2+b2
Substituting the values:
2⋅(−1√5)=√52⋅b√a2+b2
This leads to:
−2√5=√52⋅b√a2+b2
Cross-multiplying gives:
−4=5⋅b√a2+b2
Thus, we can express b in terms of a.
After determining a and b, we can find the unit vector of the refracted ray:
^R=a^i+b^j√a2+b2
After performing the calculations, we find:
^R=4^i−3^j5
The unit vector along which the refracted ray moves is:
^R=4^i−3^j5
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - B. More than one option is correct
20 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - C. comprehension type question
14 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
Similar Questions
A ray of light moving along a vector (3√2ˆi−3ˆj−3ˆk) undergoes refraction at an interface of two media which is y-z plane. The refractive index for x≤0 is 1 while for x≥0 it is √2. Then,
View SolutionThe unit vector along →A=2ˆi+3ˆj is :
View SolutionThe unit vector along →A=2ˆi+3ˆj is :
View SolutionA ray of light travelling along the line x+y=1 is incident on the X - axis and after refraction the other side of the X - axis by turning π/6 by turning away from the X - axis .The equation of the line along which the refracted ray travels is
View SolutionA ray of light is sent along the line 2x−3y=5. After refracting across the line x+y=1 it enters the opposite side after torning by 150 away from the line x+y=1 . Find the equation of the line along which the refracted ray travels.
View SolutionA ray of light is incident on a plane mirror along a vector ˆi+ˆj−ˆk.
The normal on incidence point is along ˆi+ˆj.Find a unit vector along the
reflected ray.
View Solutionx-y plane separates two media, z≥0 contains a medium of refractive index 1 and z≤0 contains a medium of refractive index 2. A ray of light is incident from first medium along a vectorˆi+ˆj−ˆk. Find the unit vector along the refracted ray.
View SolutionIn the diagram shown, light is incident on the interface between media 1 (refractive index n1) and 2 (refractive index n2) at angle slightly greater than the critical angle, and is totally reflected. The light is then also totally reflected at the interface between media 1 and 3 (refractive index n3), after which it travels in a direction opposite to its initial direction, The media must have a refractive indices such that.
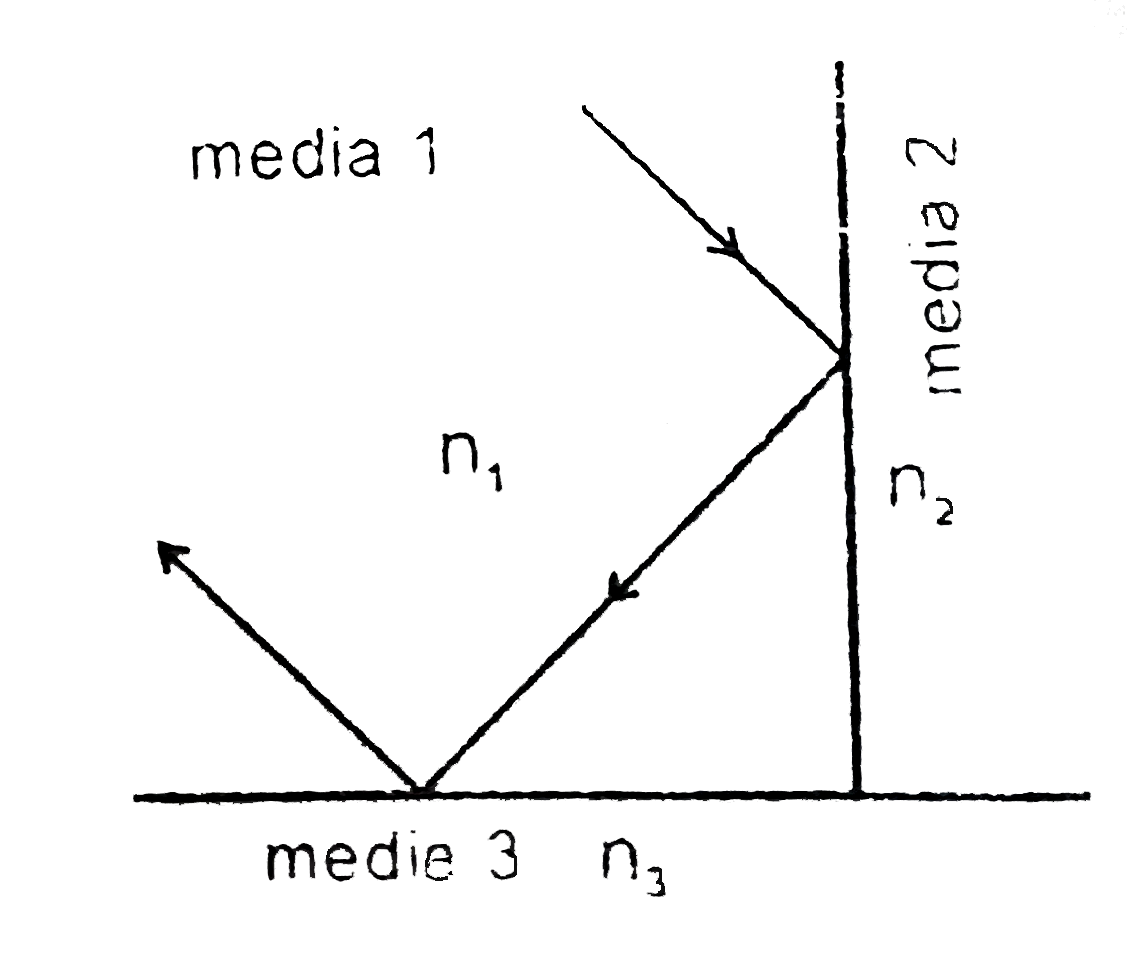 .
.
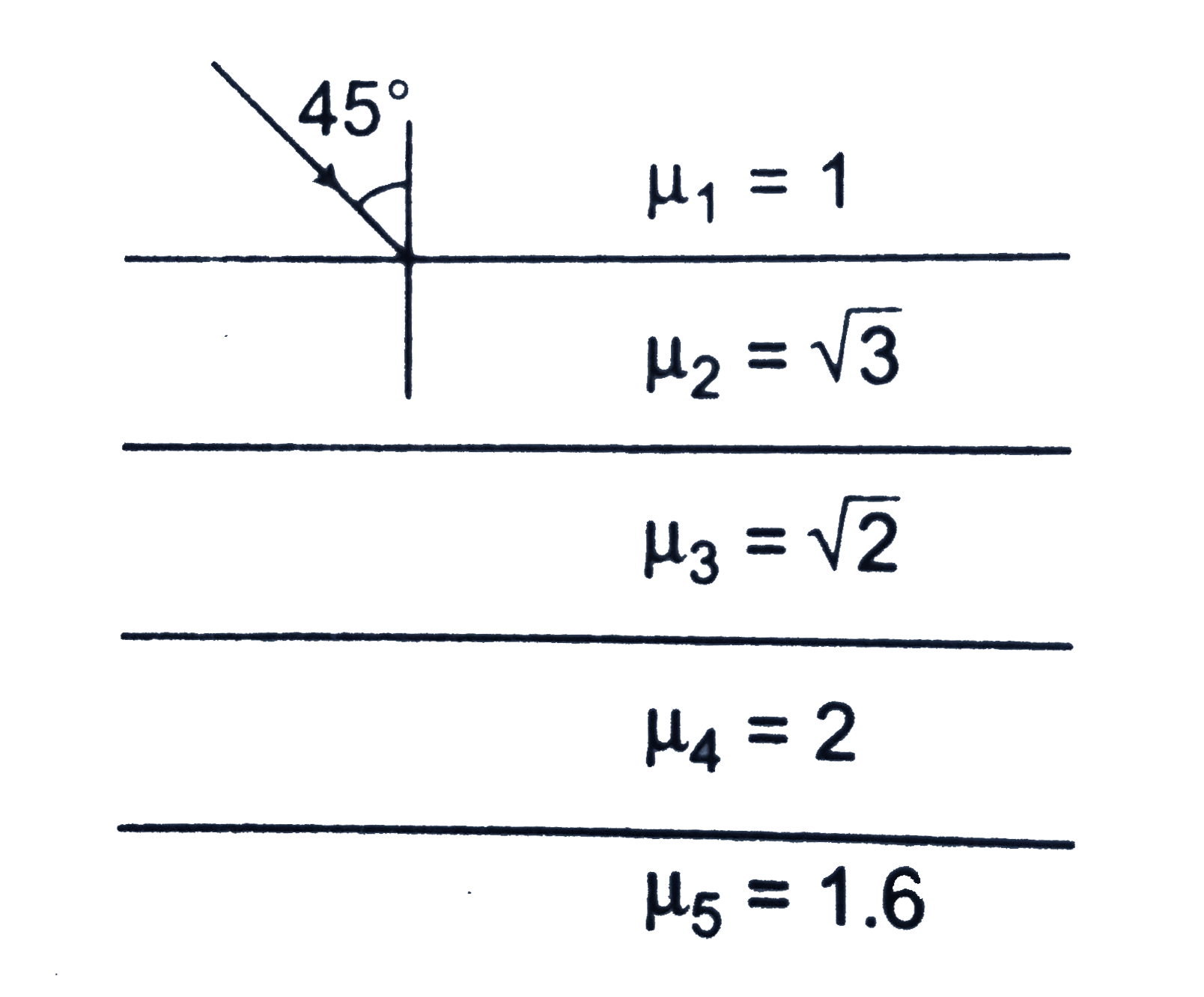
View SolutionIn the figure shown, the angle made by the light ray with the normal in the medium of refractive index √2 is
View SolutionFind the angle of deviation suffered by the light ray shown in figure. The refractive index μ=2.0 for the prism material.
View Solution
