Find the angle of deviation suffered by the light ray shown in figure. The refractive index μ=2.0 for the prism material.
The correct Answer is:B
To find the angle of deviation suffered by the light ray passing through a prism with a refractive index of μ=2.0 and an angle of prism A=4∘, we can follow these steps:
Step 1: Understand the relationship between refractive index, angle of prism, and angle of deviation
The refractive index μ of a prism is related to the angle of prism A and the angle of minimum deviation Dm by the formula:
μ=sin(A+Dm2)sin(A2)
Step 2: Substitute the known values into the formula
Given that μ=2.0 and A=4∘, we can substitute these values into the equation:
2=sin(4+Dm2)sin(42)
This simplifies to:
2=sin(2+Dm2)sin(2)
Step 3: Simplify the equation
To simplify further, we can express sin(2) as a constant value. We know that for small angles, sin(x)≈x in radians. So, we can approximate:
sin(2)≈2 (in radians)
Thus, the equation becomes:
2=sin(2+Dm2)2
Multiplying both sides by 2:
4=sin(2+Dm2)
Step 4: Solve for Dm
To find Dm, we need to isolate it:
sin(2+Dm2)=4
However, since the sine function cannot exceed 1, we must have made an error in our approximations or assumptions.
Step 5: Correct the approach
Instead, we can use the formula for small angles directly:
μ=A+DmA
Substituting the known values:
2=4+Dm4
Cross-multiplying gives:
8=4+Dm
Thus, solving for Dm:
Dm=8−4=4∘
Conclusion
The angle of deviation Dm suffered by the light ray is 4∘.
---
The refractive index μ of a prism is related to the angle of prism A and the angle of minimum deviation Dm by the formula:
μ=sin(A+Dm2)sin(A2)
Given that μ=2.0 and A=4∘, we can substitute these values into the equation:
2=sin(4+Dm2)sin(42)
This simplifies to:
2=sin(2+Dm2)sin(2)
To simplify further, we can express sin(2) as a constant value. We know that for small angles, sin(x)≈x in radians. So, we can approximate:
sin(2)≈2 (in radians)
Thus, the equation becomes:
2=sin(2+Dm2)2
Multiplying both sides by 2:
4=sin(2+Dm2)
To find Dm, we need to isolate it:
sin(2+Dm2)=4
However, since the sine function cannot exceed 1, we must have made an error in our approximations or assumptions.
Instead, we can use the formula for small angles directly:
μ=A+DmA
Substituting the known values:
2=4+Dm4
Cross-multiplying gives:
8=4+Dm
Thus, solving for Dm:
Dm=8−4=4∘
The angle of deviation Dm suffered by the light ray is 4∘.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXAMPLE9videos
GEOMETRICAL OPTICS
- BOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer18videos
GEOMETRICAL OPTICS
- BOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Objective -27videos
GEOMETRICAL OPTICS
- BOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question7videos
GAUSS LAW
- BOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer11videos
LIGHT WAVES
Similar Questions
Find the angle of devaition suffered by the light ray shown in figure for following two conditions. The refractive index for the prism material is μ=3/2.
(i) When the prism is placed in air 9μ=1)
(ii) When the prism is placed in water (μ=4/3)
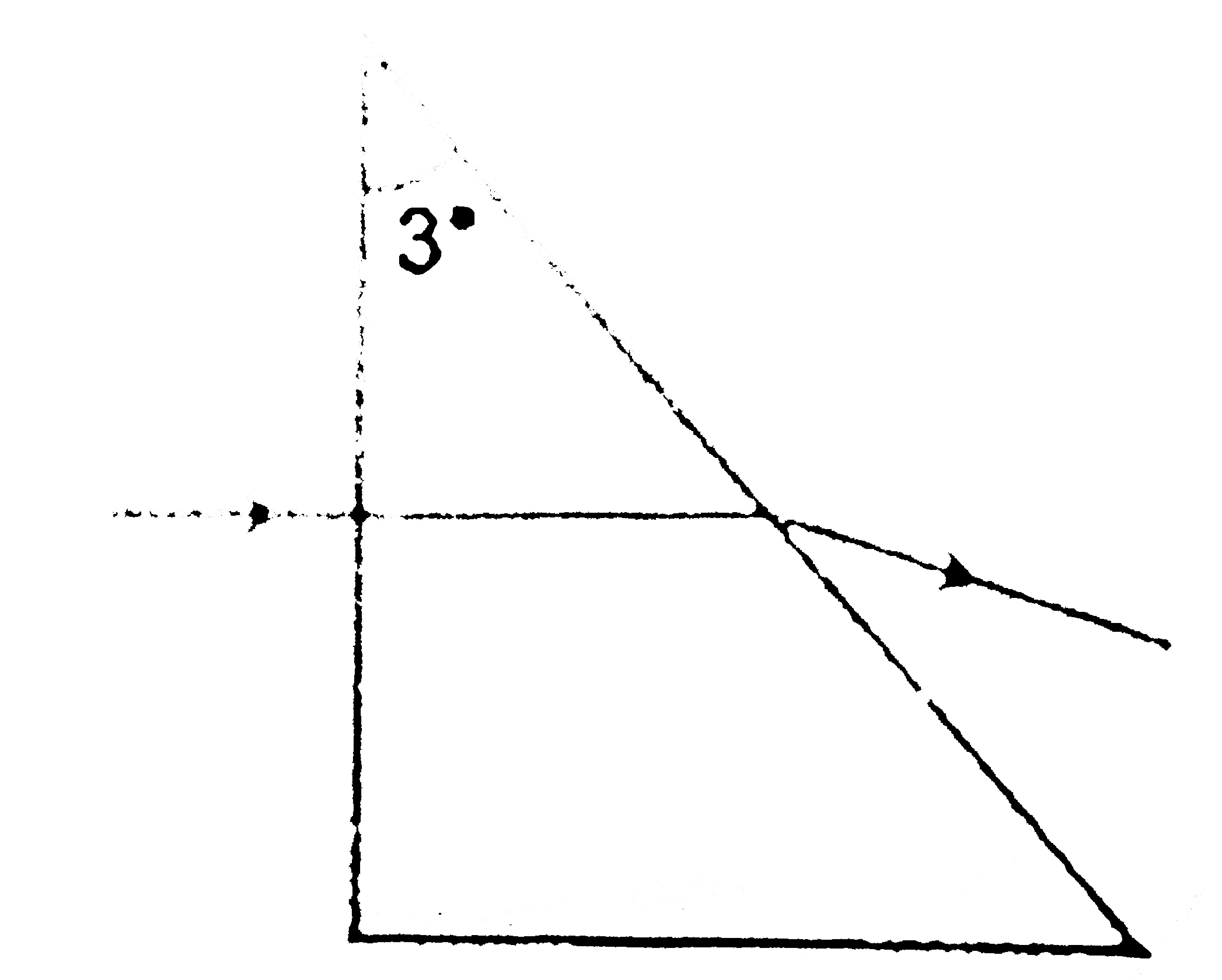 View Solution
View SolutionFind the net deviation produced in the incident ray for the optical instrument shown in figure. (Take refractive index of the prism material as 2.)
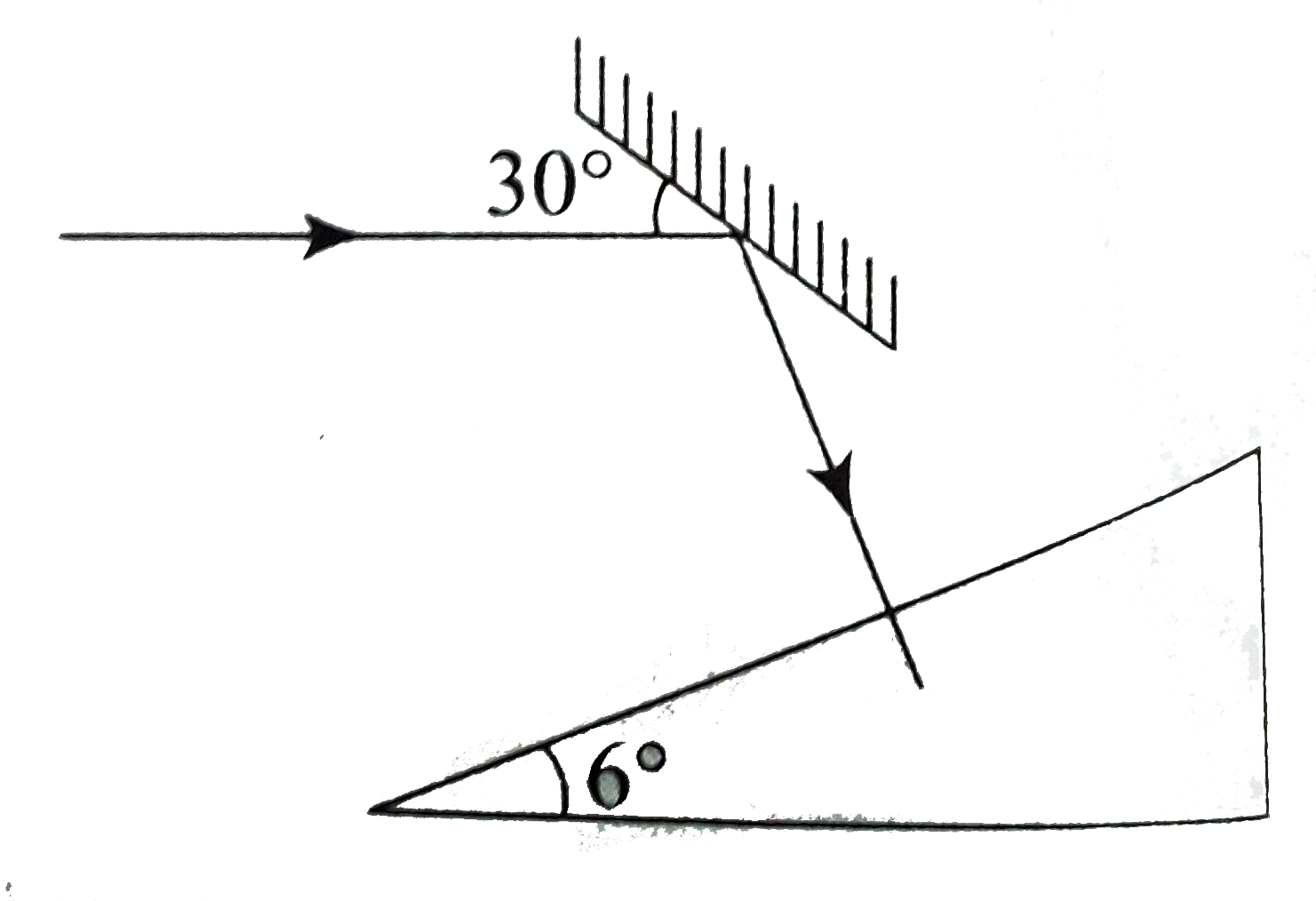 View Solution
View SolutionWhen light of wavelength λ is incident on an equilateral prism, kept on its minimum deviation position, it is found that the angle of deviation equals the angle of the prism itself. The refractive index of the material of the prism for the wavelength λ is
View SolutionA prism is made of glass of unknown refractive index. A parallel beam of light is incident on a face of the prism. By rotating the prism, the minimum angle of deviation is measured to be 40∘. What is the refractive index of the prism ? If the prism is placed in water (μ=1.33), predict the new angle of minimum deviation of the parallel beam. The refracting angle of prism is 60∘.
View SolutionIf the angle of minimum deviation is of 60∘ for an equilateral prism , then the refractive index of the material of the prism is
View Solution
A ray of light is incident normally on one face of a prism as shown in figure. The refractive index of the material of the prism is 53 and the prism is immersed in water of refractive index 43, thenView SolutionA ray of light falls on a right angled prism ABC (AB=BC) and travels as shown in figure. What is the refractive index of material of the prism ?
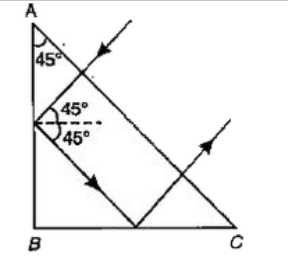 View Solution
View SolutionFind the angle of minimum deviation for an equilateral prism made of a material of refractive index 1.732. What is the angle of incidence for this deviation ?
View SolutionThe angle of minimum deviation from a prism is 37∘. If the angle of prism is 53∘, find the refractive index of the material of the prism.
View SolutionThe angles of refraction of a very thin prism is 1∘. A light say is incident normally on one of the refracting surface. The ray that ultimately emerges from the first surface, after suffering from the second surface. Makes an angle of 3.32∘ with the normal. the deviation of the ray emerging from the second surface and the refractive index of the material of the prism respectivley, are
View Solution

