A real image of an object is formed at a distance of 20cm from a lens. On putting another lens in contact with it, the image is shifted 10cm towards the combination, Determine the power of the second lens.
2D
5D
6D
10 D
The correct Answer is:B
To solve the problem step by step, we will follow these instructions:
Step 1: Understand the given information
We have a real image formed by the first lens at a distance of V1=20cm. When a second lens is placed in contact with the first lens, the image shifts 10cm towards the combination, resulting in a new image distance of V2=20cm−10cm=10cm.
Step 2: Use the lens formula for the first lens
The lens formula is given by:
1F=1V−1U
For the first lens, we can express it as:
1F1=1V1−1U
Substituting V1=20cm:
1F1=120−1U(Equation 1)
Step 3: Use the lens formula for the combination of lenses
For the combination of the two lenses, we have:
1F=1F1+1F2
Using the new image distance V2=10cm:
1F=1V2−1U
Substituting V2=10cm:
1F=110−1U(Equation 2)
Step 4: Substitute Equation 1 into Equation 2
From Equation 1, we know 1F1:
1F=110−(120−1U)
This simplifies to:
1F=110−120+1U
Step 5: Simplify the equation
Now, we can simplify the left-hand side:
110−120=2−120=120
So we have:
1F=120+1U
Now, we can cancel 1U from both sides:
1F−1U=120
Step 6: Solve for F2
Now, we know that F=F1+F2:
1F2=1F−1F1
Substituting F1=20cm:
1F2=1F−120
Since we found F=20cm:
1F2=110−120
This gives:
1F2=2−120=120
Thus, F2=20cm.
Step 7: Calculate the power of the second lens
The power P of a lens is given by:
P=1F(in meters)
Converting F2 to meters:
F2=20cm=0.2m
So,
P2=10.2=5diopters
Final Answer
The power of the second lens is 5diopters.
---
We have a real image formed by the first lens at a distance of V1=20cm. When a second lens is placed in contact with the first lens, the image shifts 10cm towards the combination, resulting in a new image distance of V2=20cm−10cm=10cm.
The lens formula is given by:
1F=1V−1U
For the first lens, we can express it as:
1F1=1V1−1U
Substituting V1=20cm:
1F1=120−1U(Equation 1)
For the combination of the two lenses, we have:
1F=1F1+1F2
Using the new image distance V2=10cm:
1F=1V2−1U
Substituting V2=10cm:
1F=110−1U(Equation 2)
From Equation 1, we know 1F1:
1F=110−(120−1U)
This simplifies to:
1F=110−120+1U
Now, we can simplify the left-hand side:
110−120=2−120=120
So we have:
1F=120+1U
Now, we can cancel 1U from both sides:
1F−1U=120
Now, we know that F=F1+F2:
1F2=1F−1F1
Substituting F1=20cm:
1F2=1F−120
Since we found F=20cm:
1F2=110−120
This gives:
1F2=2−120=120
Thus, F2=20cm.
The power P of a lens is given by:
P=1F(in meters)
Converting F2 to meters:
F2=20cm=0.2m
So,
P2=10.2=5diopters
The power of the second lens is 5diopters.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Reflection Of Light By Spherical Mirrors
5 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Refraction
10 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - ASSERTION AND REASON
15 Videos
- PRACTICE PAPPERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 3
50 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
A convex lens forms a real and inverted image of a needle at a distance of 50cm from it. Where is the needle placed in front of the convex lens if the image is equal to size of the object ? Also, find the power of the lens.
View SolutionA point object is placed at a distance of 15 cm from a convex lens. The image is formed on the other side at a distance of 30 cm from the lens. When a concave lens is placed in contact with the convex lens, the image shifts away further by 30 cm. Calculate the focal lengths of the two lenses.
View SolutionA real image is formed by a convex lens. If we put a concave lens in contact with it, the combination again forms a real image. The new image
View SolutionA convex lens forms an image of an object placed 20cm away from it at a distance of 20cm on the other side of the lens. If the object is moves 5cm toward the lens, the image will be
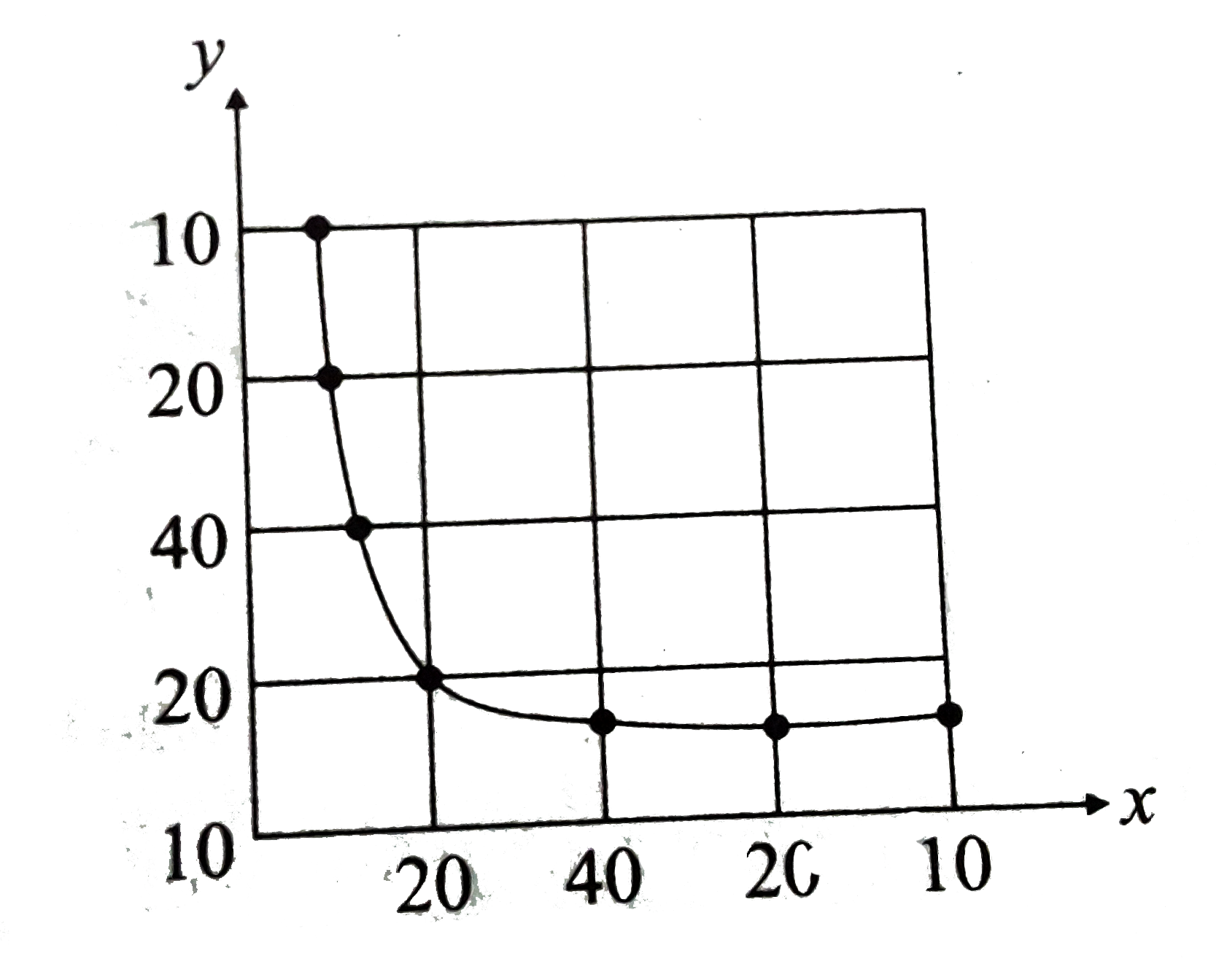
View SolutionA lens forms a real image of an object. The distance from the object to the lens is x cm and that from the lens to the image is y cm. The graph shows the variation of y with x.
It can be deduced that the lens is
View SolutionA convex lens forms an image of an object on a screen 30 cm from the lens. When the lens is moved 90 cm towards the object, then the image is again formed on the screen. Then, the focal length of the lens is
View SolutionAn object is kept at a distance of 15 cm from a convex lens of focal length 10 cm. Calculate the image distance and state the characteristics of the image formed.
View SolutionAn object is placed at a distance 24 cm in front of a convex lens of focal length 8 cm.
Calculate the distance of the image from the lens.
View SolutionAn object is kept at a distance of 16cm from a thin lens and the image formed is real. If the object is kept at a distance of 6cm from the lens, the image formed is virtual. If the sizes of the images formed are equal, the focal length of the lens will be
View SolutionWhen an object is placed 40cm from a diverging lens, its virtual image is formed 20cm from the lens. The focal length and power of lens are
View Solution
