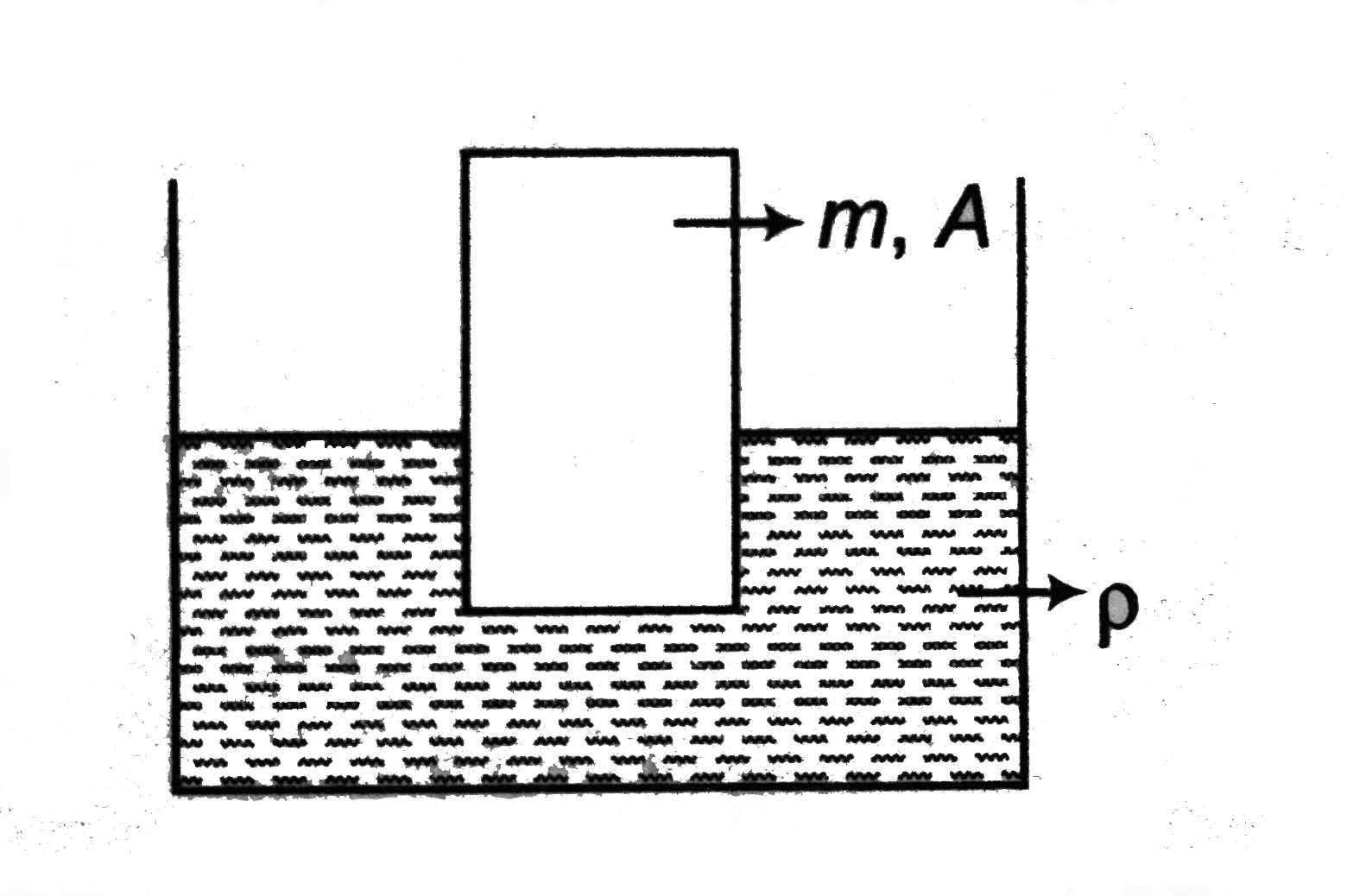
A rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period T. Then
T∝√ρ
T∝1√A
T∝1ρ
T∝1√m
The correct Answer is:B
To solve the problem, we will derive the expression for the time period T of oscillation of a rectangular block floating in a liquid when displaced vertically from its equilibrium position.
1. Understanding the Forces:
When the block is floating, it displaces a volume of liquid equal to the weight of the block. The buoyant force acting on the block is given by:
Fb=ρgV
where V is the volume of the liquid displaced. For a block of area A and depth x submerged, the volume is V=Ax. Thus, the buoyant force becomes:
Fb=ρgAx
2. Weight of the Block:
The weight of the block is:
Fg=mg
3. Equilibrium Condition:
At equilibrium, the buoyant force equals the weight of the block:
ρgAh=mg
where h is the depth of the block submerged at equilibrium.
4. Displacement from Equilibrium:
When the block is displaced by a small distance x downwards, the new submerged depth is h+x. The new buoyant force becomes:
F′b=ρgA(h+x)=ρgAh+ρgAx
5. Net Force:
The net force acting on the block when it is displaced is given by:
Fnet=F′b−Fg=ρgA(h+x)−mg
Since ρgAh=mg, we can simplify this to:
Fnet=ρgAx
6. Using Newton's Second Law:
According to Newton's second law, the net force is also equal to mass times acceleration:
Fnet=−md2xdt2
Setting these two expressions for net force equal gives:
−md2xdt2=−ρgAx
Rearranging gives:
d2xdt2+ρgAmx=0
7. Identifying the Angular Frequency:
This is a standard form of simple harmonic motion, where:
ω2=ρgAm
Thus, the angular frequency ω is:
ω=√ρgAm
8. Finding the Time Period:
The time period T of oscillation is related to the angular frequency by:
T=2πω=2π√mρgA
Final Expression:
Thus, the time period of oscillation T is given by:
T=2π√mρgA
When the block is floating, it displaces a volume of liquid equal to the weight of the block. The buoyant force acting on the block is given by:
Fb=ρgV
where V is the volume of the liquid displaced. For a block of area A and depth x submerged, the volume is V=Ax. Thus, the buoyant force becomes:
Fb=ρgAx
The weight of the block is:
Fg=mg
At equilibrium, the buoyant force equals the weight of the block:
ρgAh=mg
where h is the depth of the block submerged at equilibrium.
When the block is displaced by a small distance x downwards, the new submerged depth is h+x. The new buoyant force becomes:
F′b=ρgA(h+x)=ρgAh+ρgAx
The net force acting on the block when it is displaced is given by:
Fnet=F′b−Fg=ρgA(h+x)−mg
Since ρgAh=mg, we can simplify this to:
Fnet=ρgAx
According to Newton's second law, the net force is also equal to mass times acceleration:
Fnet=−md2xdt2
Setting these two expressions for net force equal gives:
−md2xdt2=−ρgAx
Rearranging gives:
d2xdt2+ρgAmx=0
This is a standard form of simple harmonic motion, where:
ω2=ρgAm
Thus, the angular frequency ω is:
ω=√ρgAm
The time period T of oscillation is related to the angular frequency by:
T=2πω=2π√mρgA
Thus, the time period of oscillation T is given by:
T=2π√mρgA
Topper's Solved these Questions
- OPTICS AND OPTICAL INSTRUMENTSBOOK - NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)CHAPTER - OPTICS AND OPTICAL INSTRUMENTSEXERCISE - All Questions
87 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)CHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Physical
41 Videos
Similar Questions
A plank of mass 'm' and area of cross - section A is floating as shown in figure. When slightly displaced from mean position, plank starts oscillations. Find time period of these osillations.

View SolutionA plank of mass 'm' and area of cross - section A is floating in a non - viscous liquid of desity ρ. When displaced slightly from the mean position, it starts oscillating. Prove that oscillations are simple harmonic and find its time period.
View Solution
Knowledge Check
A rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period T.
(i) T∝√m
(ii) T∝√ρ
(iii) T∝1√A
(iv) T∝1√ρ.A(i),(ii),(iii)B(i),(iii),(iv)C(i),(iii)D(iii),(iv)A rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period T. Then
AT∝√ρBT∝1√ACT∝1√ρDT∝1√mA rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period T. Then
AT∝√ρBT∝1√ACT∝1∝DT∝1√m
A rectangular block of mass m and area of cross section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium it undergoes with a time period T, then
View SolutionA block of rectangular size of mass m and area of cross section A, float in a liquid of density ρ.If we give a small vertical displacement from equilibrium, It undergoes SHM with time period T, then
View SolutionA rectangular block of mass m and area of cross a small vertical displacement from equilibrium it undergoes oscillation with a time period T then
View SolutionA cylinderical block of wood of mass m and area cross-section A is floating in water (density = ρ) when its axis vertical. When dressed a little and the released the block starts oscillating. The period oscillations is
View SolutionA body of uniform cross-sectional area floats in a liquid of density thrice its value. The portion of exposed height will be :
View Solution
