A rectangular box is completely filled with a liquid of density , as shown in Fig. The box is accelerated horizontally with a constant acceleration a. Determine the gauge pressures at the four points and .
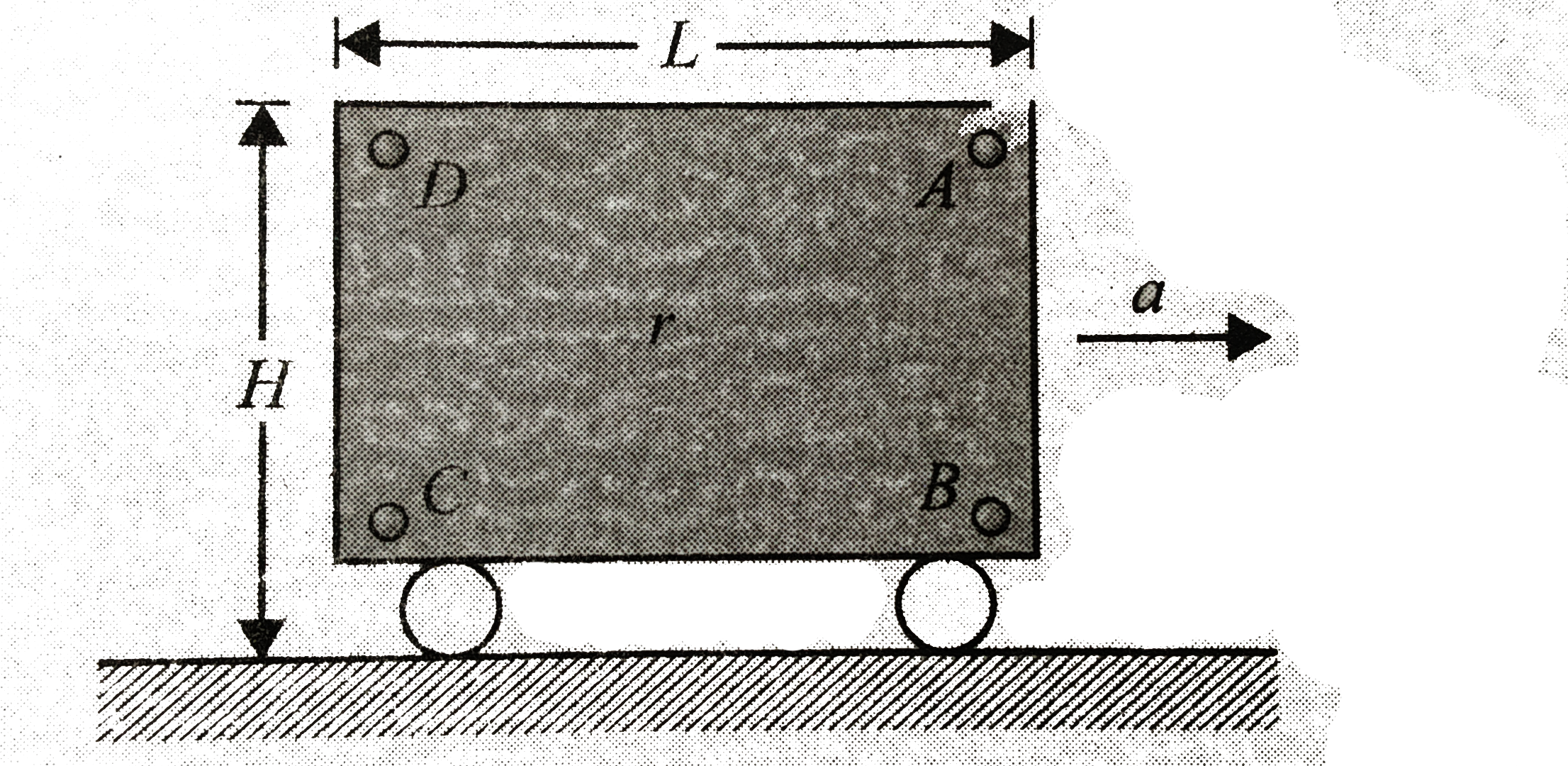
At point
At point
At point
At point
Or alternatively,
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.3
10 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.4
10 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.1
11 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
A container shown in Fig. is accelerated horizontally with acceleration a.
a. Find the minimum value of a at which liquid just starts spilling out.

View SolutionA small ball of volume V and density ρ is held inside a cubical container of side L filled with an ideal liquid of density 4ρ as .Now if the container started moving with constant acceleration a and the ball it hits the top corner point Q of the container . Then find the value of k . Given g=10m/s2
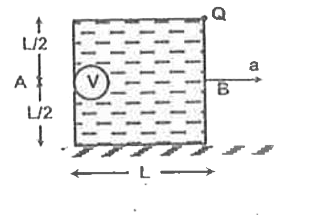
View Solution
Knowledge Check
A closed rectangular tank is completely filled with water and is accelerated horizontally with an acceleration towards the righ. Pressure is i. maximum and ii. minimum at
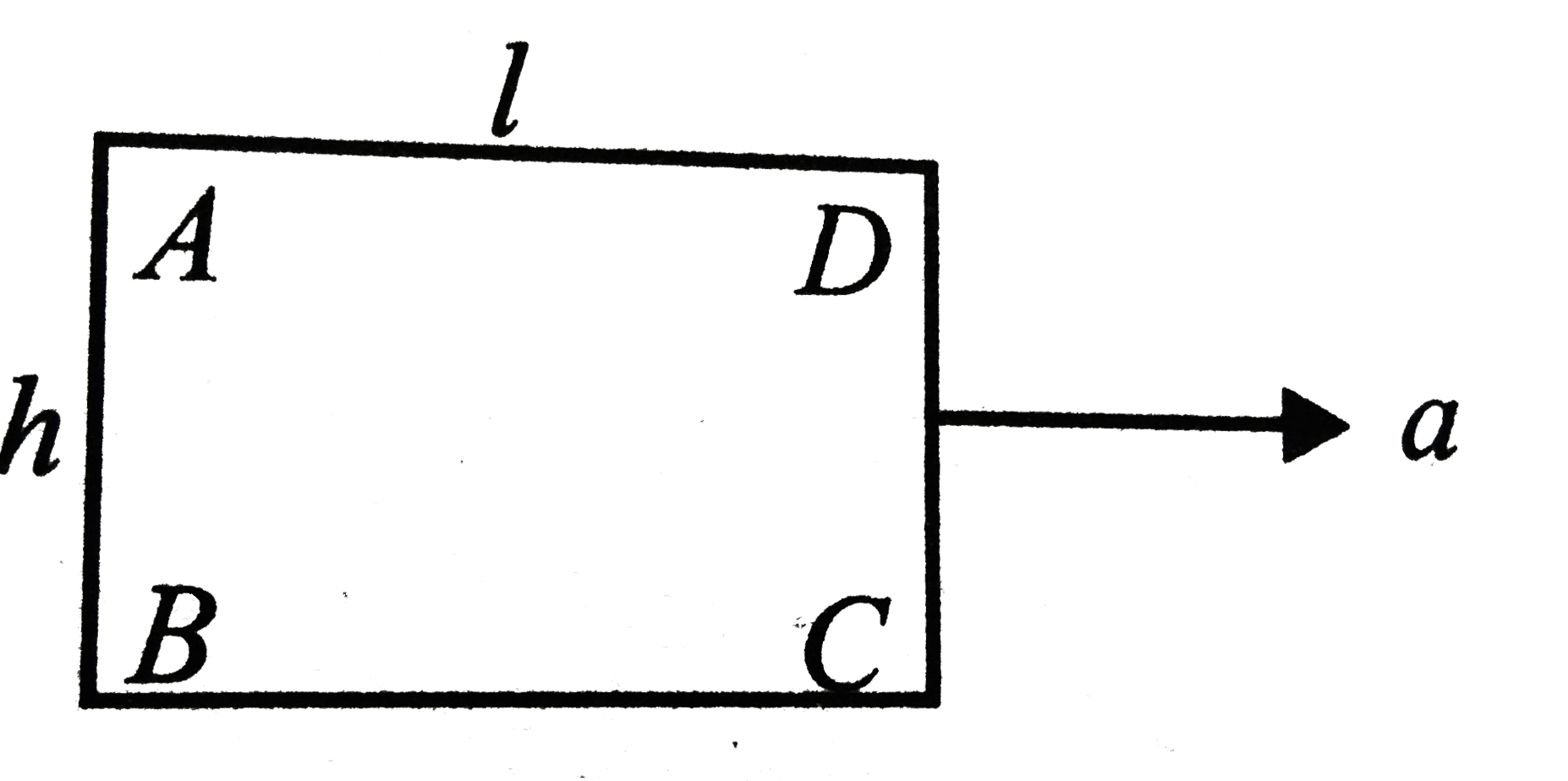 Ai. B ii DBi C ii DCi B ii CDi B ii A
Ai. B ii DBi C ii DCi B ii CDi B ii AA closed cubical box is completely filled with water and is accelerated horizontally towards right with an acceleration a. The resultant normal force by the water on the top of the box.
Apasses through the centre of topBpasses through a point to the righ of the centreCpasses through a point to the left of the centreDbecomes zeroA small solid ball of density ρ is held inside at point A of a cubical container of side L, filled with an ideal liquid of density 4ρ as shown in the figure. Now, if the container starts moving with constant acceleration a horizontally and the ball is released from point A simultaneously, then choose from following the correct option(s)
 AFor ball to hit the top of container at end Q,a=3gBFor ball to hit the top of container at end Q,a=2gCBall hits the top of container at end Q after a time t=√L3gDBall hits the top of container at end Q after a time t=√2L3g
AFor ball to hit the top of container at end Q,a=3gBFor ball to hit the top of container at end Q,a=2gCBall hits the top of container at end Q after a time t=√L3gDBall hits the top of container at end Q after a time t=√2L3g
A vessel filled with water is moving horizontally with constant acceleration w. What shape will the surface of the liquid have?
View SolutionA ball of density ais released from rest from the centre of an accelerating sealed cubical vessel completely filled with a liquid of density ρ. If the trough moves with a horizontal acceleration →a0 find the initial acceleration of the ball.
View SolutionA cubical contaienr of side length L is filled completely with water. The container is closed. It is acclerated horizontally with acceleration a. Density of water is ρ.
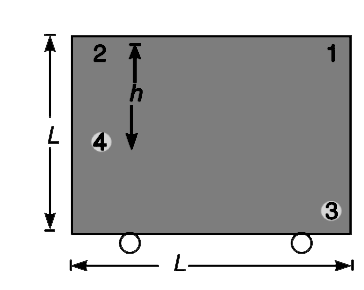
(a) Assuming pressure at point 1 (upper right corner) to be zero, find pressure at point 2 (upper left corner).
(b) Pressure at point 4, at a distance h vertically below point 2 , is same as pressure at lower right corner 3. find h.
View SolutionA closed rectangular vessel completely filled with a liquid of density ρmoveswithanae≤rationa=g.Thevalueofthepressrured⇔erenceatp∮AandBi.e.,(P_1 -P_2) is :

View Solution
A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B is
View Solution
