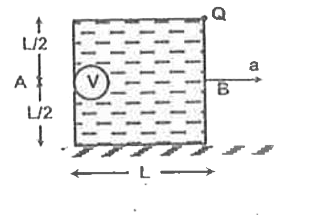
A small ball of volume V and density $ρ$ is held inside a cubical container of side L filled with an ideal liquid of density $4 ρ$ as .Now if the container started moving with constant acceleration a and the ball it hits the top corner point Q of the container . Then find the value of k . Given $g = 10 m / s^{2}$

Text Solution

Verified by Experts

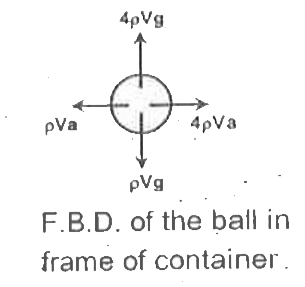
Acceleration of the ball in y direction will be $a_{y} = \frac{4 ρ V g - ρ V g}{ρ V} = 3 g$
For the ball to hit the top of the container
$\frac{L}{2} = \frac{1}{2} 3 {gt}^{2} \Rightarrow t - \sqrt{\frac{L}{3 g}}$
In the frame of container , along the container
$\frac{4 δ_{a} - δ v_{a}}{δ v} = 3 a, \frac{1}{2} 3 a t^{2} = L$
$\Rightarrow a = 2 g$

|

Updated on:21/07/2023

Class 12 PHYSICS FLUID MECHANICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
A small solid ball of density $ρ$ is held inside at point A of a cubical container of side L, filled with an ideal liquid of density $4 ρ$ as shown in the figure. Now, if the container starts moving with constant acceleration a horizontally and the ball is released from point A simultaneously, then choose from following the correct option(s)

AFor ball to hit the top of container at end $Q, a = 3 g$
BFor ball to hit the top of container at end $Q, a = 2 g$
CBall hits the top of container at end Q after a time $t = \sqrt{\frac{L}{3 g}}$
DBall hits the top of container at end Q after a time $t = \sqrt{\frac{2 L}{3 g}}$
Question 2 - Select One
A ball of density $ρ$ is released from deep inside of a liquid of density $2 ρ$ . It will move up
Awith an increasing acceleration
Bwith a decreasing acceleration
Cwith a constant acceleration
Dwith zero acceleration
Question 3 - Select One

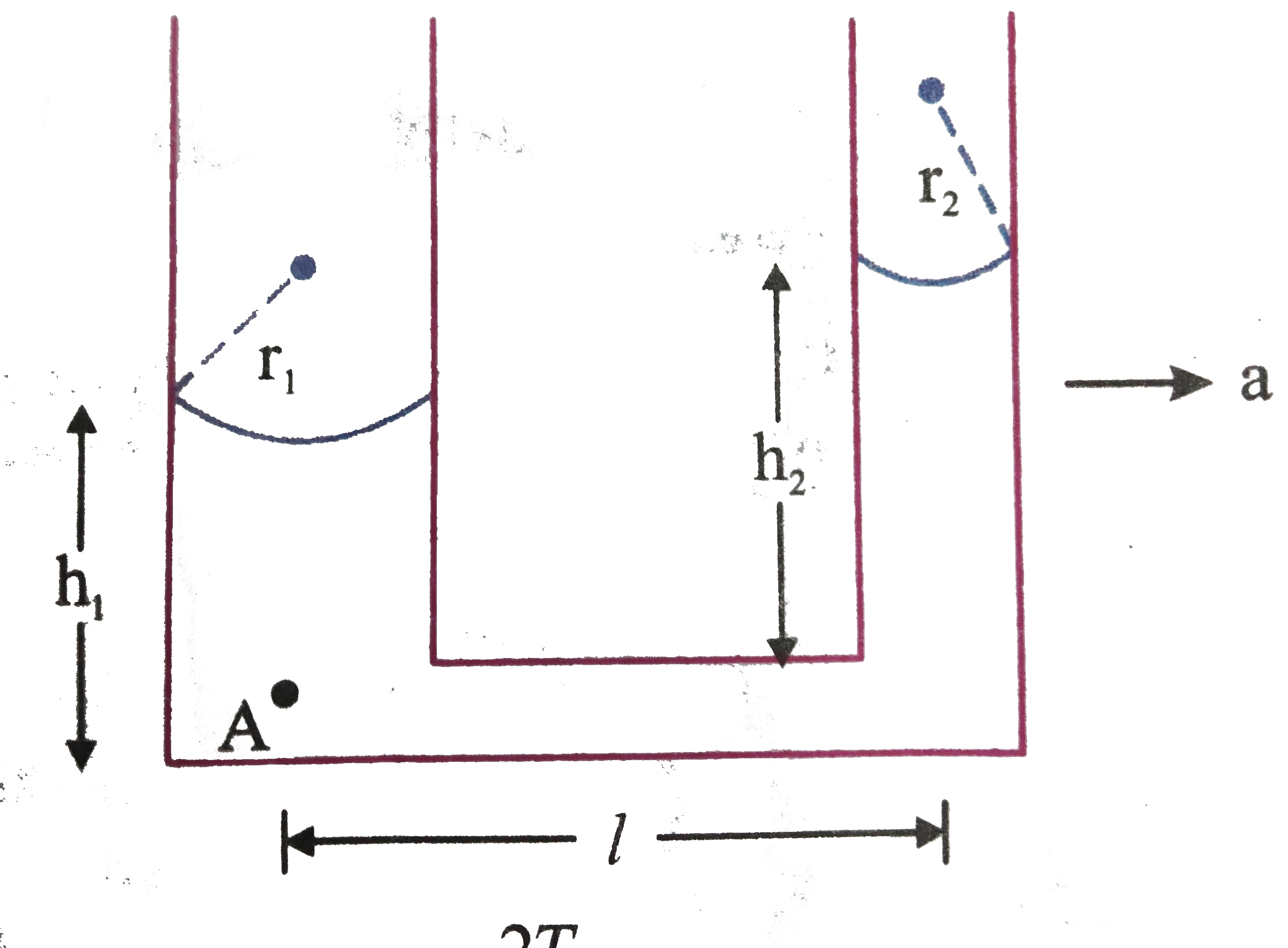
A vertical communicating tube contains a liquid of density $ρ$ . If it moves with a horizontal acceleration $a$ , pressure at $A$ is equal to :
A $ρ g h_{2} + P_{0} + \frac{2 T}{r_{2}} + ρ a l$
B $ρ g h_{2} + ρ a l + P_{0} - \frac{2 T}{r_{2}}$
C $ρ g h_{1} + P_{0} - \frac{2 T}{r_{1}}$
D $ρ g h_{1} - P_{0} - \frac{2 T}{r_{1}}$

FIITJEE-FLUID MECHANICS -NUMERICAL BASED QUESTIONS

Home
Ask Doubt
Profile