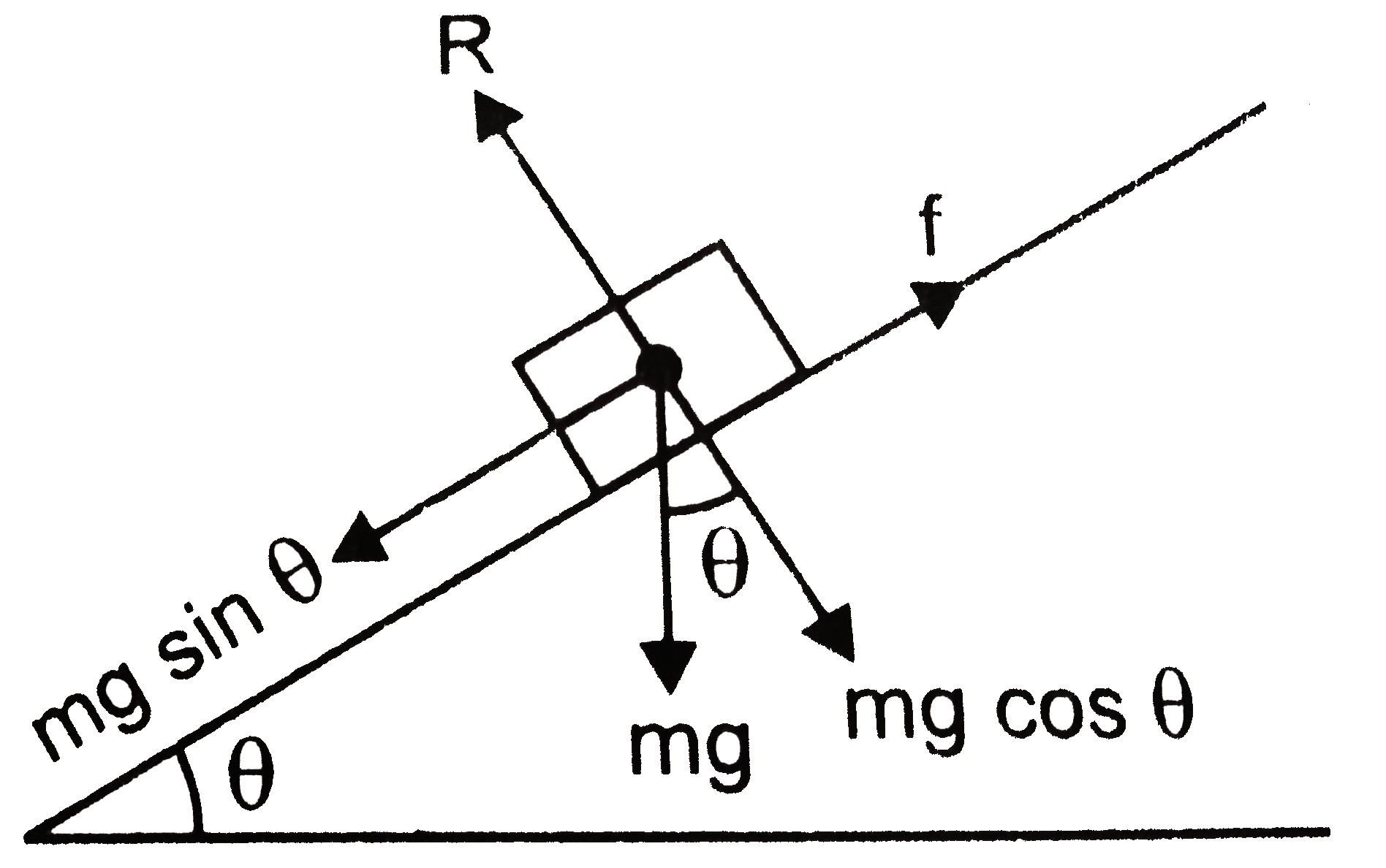
A rectangular box lies on a rough inclined surface . The coefficient of friction between the surface and the box is $μ$ . Let the mass of the box be m .
(a) At what angle of inclination $θ$ of the plane to the horizontal will the box just start to slide down the plane ?
(b) What is the force acting on the box down the plane , if the angle of inclination of the plane is increased to $α > θ$ ?
(c) What is the force needed to be applied upwards along the plane to make the box either remain stationary or just move up with uniform speed ?
(d) What is the force needed to be applied upwards along the plane to make the box move up the plane with acceleration a ?

Video Solution

Text Solution

Verified by Experts

(a) As the box tends to slide down force of friction will act up the plane
As is clear from box will just start slidding down , when
$m g sin θ = f = μ R = μ m g cos θ$
or $tan θ = μ or θ = {tan}^{- 1} (μ)$
(b) When angle of inclination is increased to $α > θ$ then net force acting on the box down the plane is
$F_{1} = m g sin α - f = m g sin α + f = m g (sin α + μ cos α)$
(In this case friction would act down the plane ) (d) If the box is to be moved with an upward acceleration a then upward force needed
$F_{3} = m g (sin α + μ cos α) + m a$
.

Updated on:21/07/2023