A rigid bar of mass 15 kg is supported symmetrically by three wires each 2 m long. Those at each end aer of copper and middle one is of iron. Determine the ratio of their diameters if each is to have the same tensoin. Young's modulus of elasticity for copper and steel are 110×109Nm−2 and 190×109Nm−2 respectively.
To solve the problem of determining the ratio of the diameters of the copper and iron wires supporting a rigid bar, we will follow these steps:
Step 1: Understand the Problem
We have a rigid bar of mass 15 kg supported symmetrically by three wires: two copper wires at the ends and one iron wire in the middle. Each wire is 2 m long, and we need to find the ratio of their diameters if each wire experiences the same tension.
Step 2: Identify Given Data
- Mass of the rigid bar (m) = 15 kg
- Length of each wire (L) = 2 m
- Young's modulus for copper (E_cu) = 110×109N/m2
- Young's modulus for iron (E_fe) = 190×109N/m2
Step 3: Establish the Relationship
Since each wire has the same tension (T) and experiences the same extension (ΔL), we can use the relationship provided by Young's modulus (E), which is defined as:
E=StressStrain=F/AΔL/L
Where:
- Stress = FA=TA
- Strain = ΔLL
Step 4: Express Area in Terms of Diameter
The cross-sectional area (A) of a wire can be expressed in terms of its diameter (D):
A=πD24
Step 5: Set Up the Equations
For both materials, we can write:
For copper:
Ecu=TπD2cu4⋅ΔLL
For iron:
Efe=TπD2fe4⋅ΔLL
Since the tension (T), length (L), and extension (ΔL) are the same for both wires, we can simplify the equations:
Ecu∝1D2cu
Efe∝1D2fe
Step 6: Relate the Diameters
From the proportional relationships, we can set up the ratio of the diameters:
D2cuD2fe=EfeEcu
Taking the square root gives us:
DcuDfe=√EfeEcu
Step 7: Substitute the Values
Substituting the values of Young's modulus:
DcuDfe=√190×109110×109=√190110=√1.727≈1.31
Step 8: Final Ratio
Thus, the ratio of the diameters of the copper wire to the iron wire is approximately:
DcuDfe≈1.31
Conclusion
The ratio of the diameters of the copper wire to the iron wire is approximately 1.31.
---
We have a rigid bar of mass 15 kg supported symmetrically by three wires: two copper wires at the ends and one iron wire in the middle. Each wire is 2 m long, and we need to find the ratio of their diameters if each wire experiences the same tension.
- Mass of the rigid bar (m) = 15 kg
- Length of each wire (L) = 2 m
- Young's modulus for copper (E_cu) = 110×109N/m2
- Young's modulus for iron (E_fe) = 190×109N/m2
Since each wire has the same tension (T) and experiences the same extension (ΔL), we can use the relationship provided by Young's modulus (E), which is defined as:
- Stress = FA=TA
- Strain = ΔLL
The cross-sectional area (A) of a wire can be expressed in terms of its diameter (D):
For both materials, we can write:
Ecu=TπD2cu4⋅ΔLL
Efe=TπD2fe4⋅ΔLL
Efe∝1D2fe
From the proportional relationships, we can set up the ratio of the diameters:
Substituting the values of Young's modulus:
Thus, the ratio of the diameters of the copper wire to the iron wire is approximately:
The ratio of the diameters of the copper wire to the iron wire is approximately 1.31.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Higher Order thinking skells17videos
PROPERTIES OF BULK MATTER
- BOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Value Based Question5videos
PROPERTIES OF BULK MATTER
- BOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Advanced problems for competitions21videos
PROPERTIES OF BULK MATTER
- BOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance18videos
PHYSICAL WORLD AND MEASUREMENT
- BOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)25videos
RAY OPTICS
Similar Questions
A block of weight 100 N is suspended by copper and steel wires of same cross sectional area 0.5cm2 and, length √3 m and 1m, respectively. Their other ends are fixed on a ceiling as shown in figure. The angles subtended by copper and steel wires with ceiling are 30∘and60∘, respectively. If elongation in copper wire is (ΔlC) and elongation in steel wire is (Δls), then the ratio ΔlCΔls is -
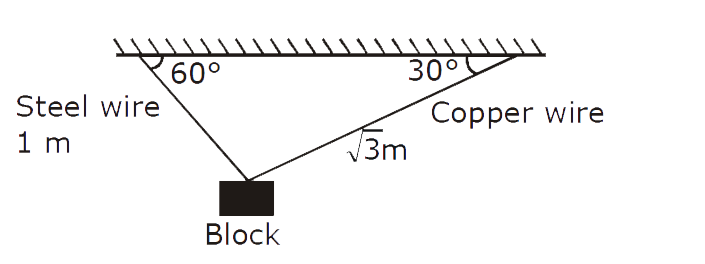
[Young's modulus for copper and steel are 1×1011N/m2and2×1011N/m2, respectively]View SolutionCompute the elongation of the steel wire in the figure. Unloaded length of the steel wire =1.5 m, the diameter of the wire is 0.25 m, Young's modulus of steel is 2×1011 N m−2.
View Solution
Knowledge Check
- Question 1 - Select One
A rigid bar of mass M is supported symmetrically by three wires each of length l. Those at each end are of copper and the middle one is of iron. The ratio of their diameters, if each is to have the same tension, is equal to
AYcopper/YironB√YironYcopperCY2ironY2copperDYironYcopper - Question 2 - Select One
A rigid bar of mass M is supported symmetrically by three wires each of length l. Those at each end are of copper and the middle one is of iron. The ratio of their diameters, if each is to have the same tension, is equal to
AYcopperYironB√YironYcopperCY2ironY2copperDYironYcopper - Question 3 - Select One
A rigid bar of mass M is supported symmetrically by three wires each of length l. Those at each end are of copper and the middle one is of ion. The ratio of their diameters, if each is to have the same tension, is equal to
AYcopper/YironB√YironYcopperCY2ironY2copperDYironYcopper
Choose the most appropriate option.
A rigid bar of mass 15 kg is supported symmetrically by three wires each 2 m long. Those at each end are of copper and the middle one is of iron. Determine the ratio of their diameters if each is to have the tension.View SolutionA rigid bar of mass M is supported symmetrically by three wires each of length I. Those at each end are of copper and the middle one is of iron. What is the ratio of their diameters DcopperDiron if each wire is to have ratio same tension?
View SolutionA rigid bar of mass 15 kg is supported symmetrically by three wires, each of length 2 m. The wires at the endpoints are made of copper and the middle one is made of steel. If the tension in each wire is the same, then the diameter of copper wire to the diameter of steel wire is [Given, Ycopper=1.1×1011N m−2andYsteel=1.9×1011N m−2]
View SolutionSteel and copper wires of same length are stretched by the same weight one after the other. Young's modulus of steel and copper are 2×1011Nm2 and 1.2×1011Nm2. The ratio of increase in length is
View SolutionIf a wire of length 4 m and cross-sectional area of 2 m2 is stretched by a force of 3 kN, then determine the change in length due to this force, Given, Young's modulus of material of wire is 110×109Nm−2
View Solution

