A block of weight 100 N is suspended by copper and steel wires of same cross sectional area 0.5cm2 and, length √3 m and 1m, respectively. Their other ends are fixed on a ceiling as shown in figure. The angles subtended by copper and steel wires with ceiling are 30∘and60∘, respectively. If elongation in copper wire is (ΔlC) and elongation in steel wire is (Δls), then the ratio ΔlCΔls is -
![A block of weight 100 N is suspended by copper and steel wires of same cross sectional area 0.5 cm^(2) and, length sqrt(3) m and 1m, respectively. Their other ends are fixed on a ceiling as shown in figure. The angles subtended by copper and steel wires with ceiling are 30^(@) and 60^(@), respectively. If elongation in copper wire is (Delta l(C)) and elongation in steel wire is (Delta l(s)), then the ratio (Delta l(C))/(Delta l(s)) is - [Young's modulus for copper and steel are 1 xx 10^(11) N//m^(2) and 2 xx 10^(11) N//m^(2), respectively]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/MOT_CON_JEE_PHY_C17_E04_027_Q01.png)
[Young's modulus for copper and steel are 1×1011N/m2and2×1011N/m2, respectively]
2
Topper's Solved these Questions
- ELASTICITY AND THERMAL EXPANSIONBOOK - MOTIONCHAPTER - ELASTICITY AND THERMAL EXPANSIONEXERCISE - Exercise - 4 (Level-I)
16 Videos
- ELASTICITYBOOK - MOTIONCHAPTER - ELASTICITYEXERCISE - EXERCISE -3
60 Videos
- Electrical Instrument BOOK - MOTIONCHAPTER - Electrical Instrument EXERCISE - EXERCISE -3
16 Videos
Similar Questions
A weight of 100N is suspended by two wires made by steel and copper as shown in figure length of steel wire is 1m and copper wire is √3m. Find ratio of change in length of copper wire (Δlc) to change in length of steel wire (Δls). given Young's modulus YSteel=2×1011N/m2,YCopper=1×1011N/m2
_PHY_E01_017_Q01.png)
View SolutionCompute the elongation of the steel wire in the figure. Unloaded length of the steel wire =1.5 m, the diameter of the wire is 0.25 m, Young's modulus of steel is 2×1011 N m−2.
View Solution
Knowledge Check
A mild steel wire of length 2L and cross-sectional area A is stretched, well with in the elastic limit, horizontally between two pillars as shown in figure. A mass m is suspended from the mid-point of the wire strain in the wire is
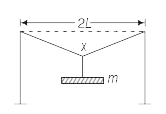 Ax22L2BxLCx2LDx22L
Ax22L2BxLCx2LDx22LIn the above question the ratio of the elongation produced in the copper wire and steel wire are
A7:2B5:2C2:5D5:7Two wires of equal cross-section but one made of steel and the other of copper are joined end to end. When the cobination is kept under tension, the elongations in the two wires are found to be equal elongations in the two wire are found to be equal. What is the ratio of the lengths of the two wires?
(Given, Young's modulus of steel =2×1011Nm−2 and young's modulus of copper =1.1×1011Nm−2)A2:11B11:2C20:11D11:20
A copper wire of length 1.0 m and a steel wire of length0.5 m having equal cross-sectional areas are joined end to end. The composite wire is stretched by a certain load which stretches the copper wire by 1mm. If the Young’s modulii of copper and steel are respectively 1.0×1011Nm−2and2.0×1011Nm−2,
the total extension of the composite wire is:
View SolutionYoung's modulus of brass and steel are 10×1010N/m and 2×1011N/m2, respectively. A brass wire and a steel wire of the same length are extended by 1mm under the same force. The radii of the brass and steel wires are RB and RS. respectively. Then
View SolutionSteel and copper wires of same length are stretched by the same weight one after the other. Young's modulus of steel and copper are 2×1011Nm2 and 1.2×1011Nm2. The ratio of increase in length is
View Solutionl-V characteristic of a copper wire of length Land area of cross-section A is shown in figure. The slope of the curve becomes
View SolutionThree copper wires of length and cross-sectional areas are (L,A)(2L,A2),(L/2,2A), resistance is
View Solution
