A rigid rod of mass m slides along a fixed circular track followed by a flat track. At the given instant, velocity of end B is v along horizontal plane. Then at the given instant:

angular speed of rod is vr
velocity of centre of mass is v√2
angular momentum of rod about O is 23mvr
kinetic energy of rod is mv26
The correct Answer is:A, B, C
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Comprehension Type Questions
41 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Matrix Matching Type Questions
17 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - A Only One Option is Correct
86 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
Similar Questions
A particle of mass 'm' is moving along a circle of radius 'r'. At some instant, its speed is 'v' and it is gaining speed at a uniform rate'a', then, at the given instant, acceleration of the particle is :
View SolutionA block of mass m is placed on a vertical fixed circular track and then it is given velocity v along the track at position A on track. The coefficient of friction between the block and the track varies with the angle θ . If the block moves on track with constant speed then the coefficient of friction is
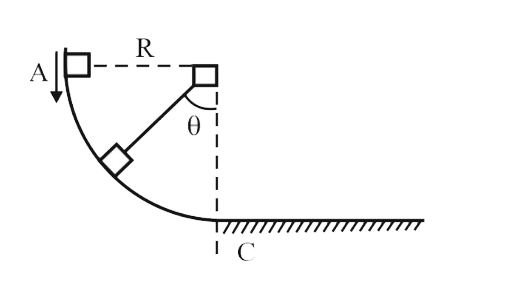
View Solution
Knowledge Check
A particle of mass 'm' is moving along a circle of radius 'r'. At some instant, its speed is 'v' and it is gaining speed at a uniform rate'a', then, at the given instant, acceleration of the mparticle is :
Aalong the radiusBinclined to radius at θ=sin−11[1+v4a2r2]1/2Cinclined to radius at θ=cos−1(ar)v2Dinclined to radius at θ=tan−1(v2)arA block of mass m is placed on a vertical fixed circular track and then it is given velocity v along the track at position A on track. The coefficient of friction between the block and the track varies with the angle θ . If the block moves on track with constant speed then the coefficient of friction is
 Aμ=sinθcotθ+v2RgBμ=sinθcosθ+v2RgCμ=tanθcosθ+v2RgDμ=cosθtanθ+v2Rg
Aμ=sinθcotθ+v2RgBμ=sinθcosθ+v2RgCμ=tanθcosθ+v2RgDμ=cosθtanθ+v2RgThe ride is circus rides along a circular track in a vertical plane. The minimum velocity at the highest point of the track will be
A√(2gR)B√(5gR)C√(3gR)D√(gR)

The smooth ring A can slide on a fixed horizontal rod as shown the pulley is fixed. If some instant velocity of ring is v, find the velocity of block at that instant.
View SolutionA block of mass m is placed on a circular track and then it is given a velocity υ vertically downwards at position A on track. If block moves on track with constant speed, then

View SolutionA particle of mass m slides along a curved-flat-curved track. The curved portions of the track are smooth. If the particle is released at the top of one of the curved portions, the particle comes to rest at flat portion of length l and of μ=μkinetic after covering a distance of
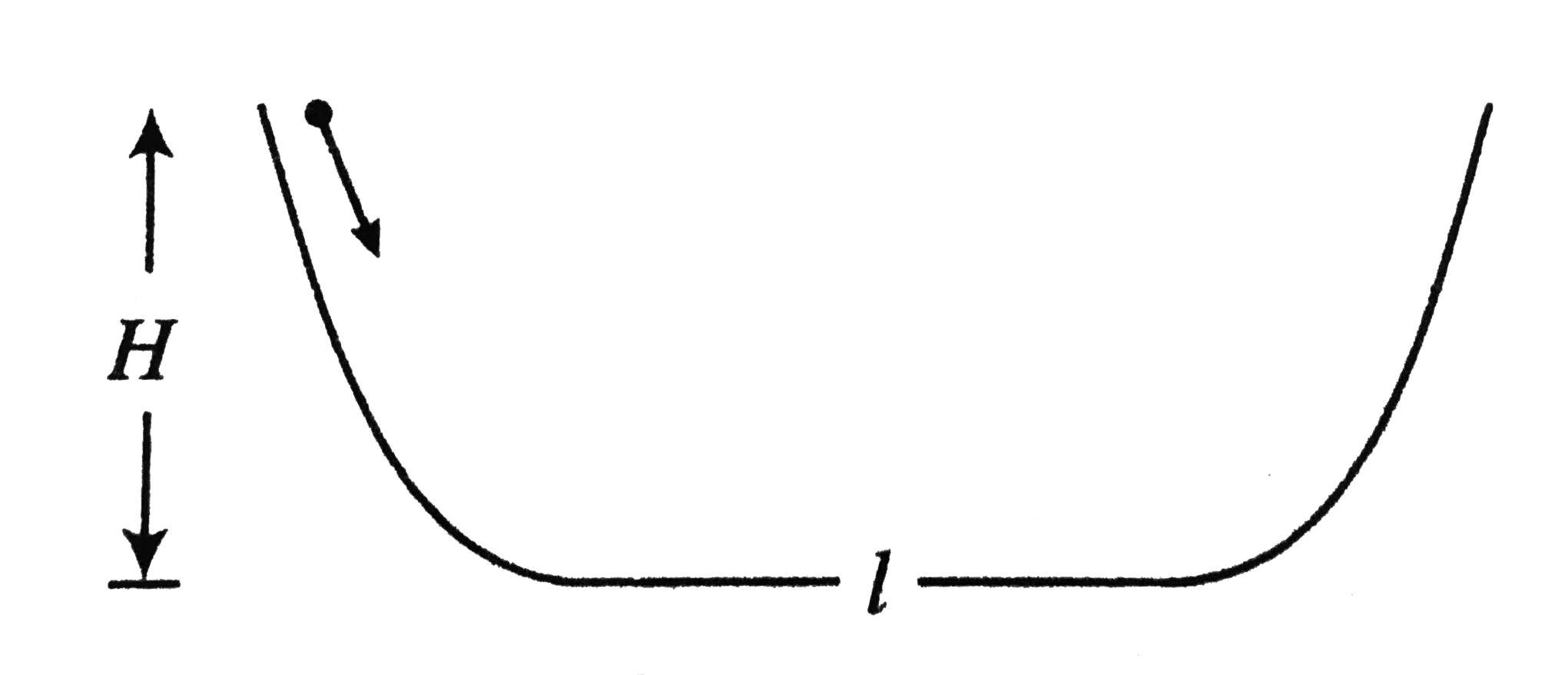
View SolutionA block of mass m is placed on a circular track and then it is given a velocity υ vertically downwards at position A on track. If block moves on track with constant speed, then

View SolutionA particle of mass m slides along a curved-flat-curved track. The curved portions of the track are smooth. If the particle is released at the top of one of the curved portions, the particle comes to rest at flat portion of length l and of μ=μkinetic after covering a distance of

View Solution
