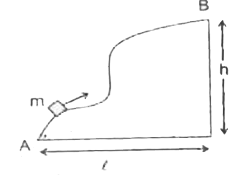
A particle of mass m slides along a curved-flat-curved track. The curved portions of the track are smooth. If the particle is released at the top of one of the curved portions, the particle comes to rest at flat portion of length l and of μ=μkinetic after covering a distance of
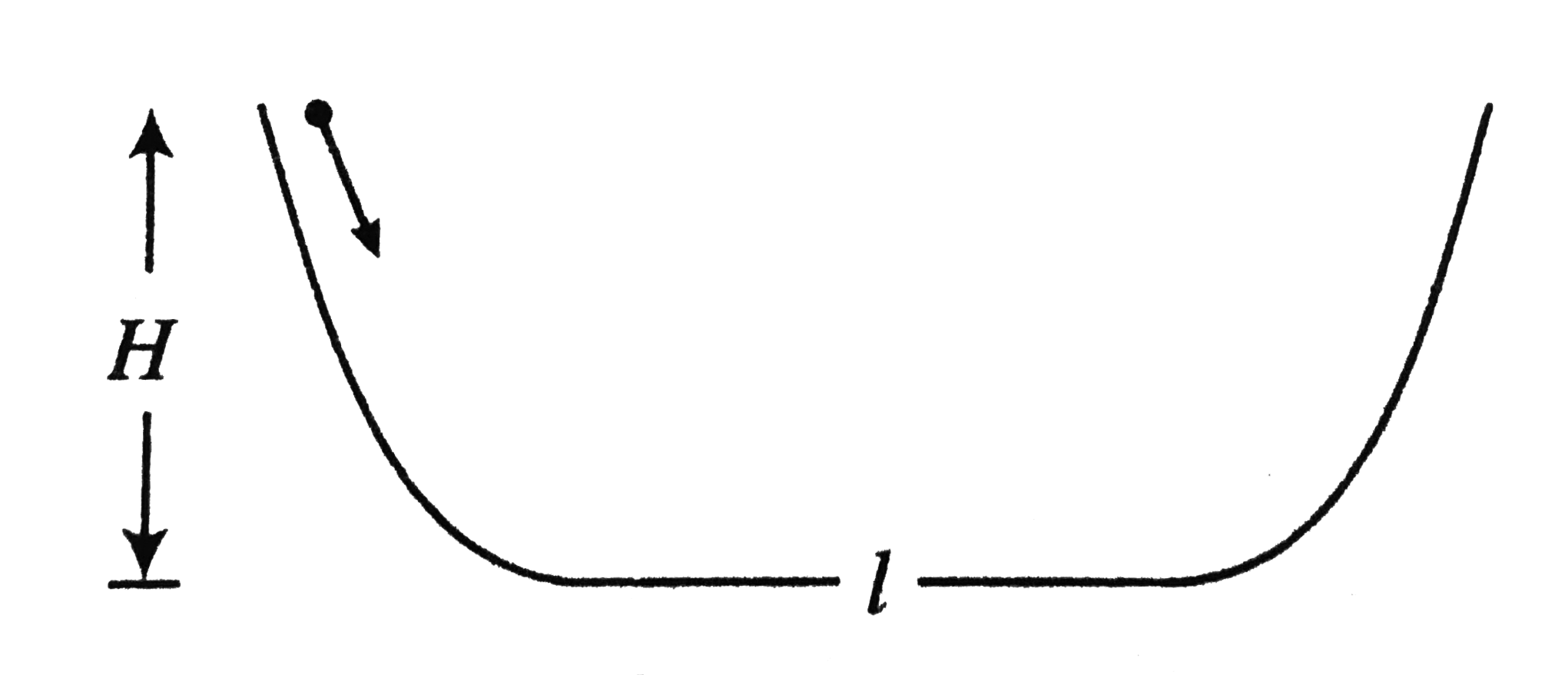
(a) l3μ
(b) H2μkinetic
(c) l6
(d) Hμkinetic
The correct Answer is:D
Here PE=Work done
mgH=μkineticmgS or S=Hμkinetic
The particle covers the length l or not or covers it repeatedly is determined by the above relation.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Multiple Correct25videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Linked Comprehension55videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Subjective23videos
WORK, POWER & ENERGY
- BOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
Two charged particle of equal mass are constrained to move along X and Y direction. The X – Y plane is horizontal and the tracks are smooth. The particles are released from rest when they were at positions shown in the figure. At the instant distance of q becomes 2r from the origin, find the location of charge Q.
 View Solution
View SolutionA rod AB of mass M and length L is lying on a horizontal frictionless surface. A particle of mass m travelling along the surface hits the end A of the rod with a velocity v0 in a direction perpendicular to AB. The collision in elastic. After the collision the particle comes to rest
(a). Find the ratio m/M
(b). A point P on the rod is at rest immediately after collision find the distance AP.
(c). Fid the linear speed of the point P a time πL/3v0 after the collision.View Solution
Knowledge Check
- Question 1 - Select One

The curved portions are smooth and horizontal surface is rough. The block is released from P. At what distance from A it will stop?A1 mB2 mC3 mD4 m - Question 2 - Select One
A point particle of mass m, moves long the uniformly rough track PQR as shown in figure. The coefficient of friction, between the particle and the rough track equals μ. The particle is released, from rest from the point P and it comes to rest at a point R. The energies, lost by the ball, over the parts, PQ and QR, of the track, are equal to each other, and no energy is lost when particle changes direction from PQ to QR.
The value of the coefficient of friction μ and the distance x (=QR), are, respectively close to:
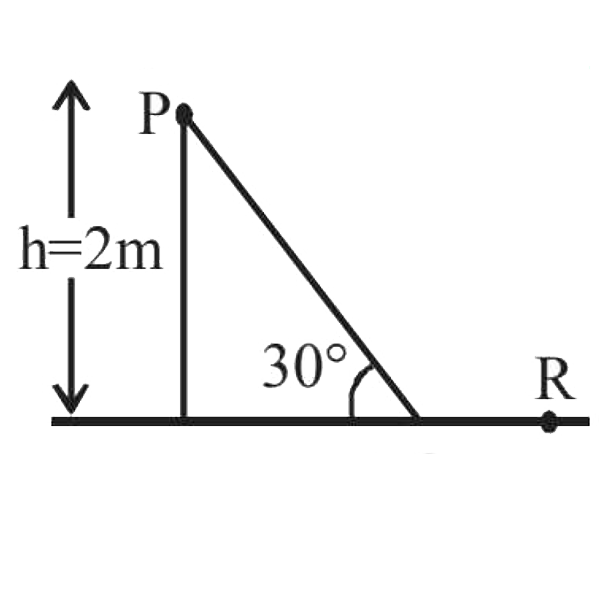 A(a) 0.29 and 3.5mB(b) 0.29 and 6.5mC(c) 0.2 and 6.5mD(d) 0.2 and 3.5m
A(a) 0.29 and 3.5mB(b) 0.29 and 6.5mC(c) 0.2 and 6.5mD(d) 0.2 and 3.5m - Question 3 - Select One
If a particle of mass m start from along curved circular path shown in figure with constant tangential acceleration a, then net force at B on the particle has the magnitude :
 AzeroB2ma√1+π2Cma√1+π2Dmaπ√1+π
AzeroB2ma√1+π2Cma√1+π2Dmaπ√1+π
A particle slides along a track with elevated ends and a flat central part as shown in figure. The flat part has a length l=3m. The curved portions of the track are frictionless. For the flat part, the coefficient of kinetic friction is μk=0.2. The particle is released at point A which is at height h=1.5m above the flat part of the track. Where does the particle finally come to rest?
 View Solution
View SolutionA particle slides along a track with elevated ends and a flat central part as shown in figure. The flat part has a length l=3m. The curved portions of the track are frictionless. For the flat part, the coefficient of kinetic friction is μk=0.2. The particle is released at point A which is at height h=1.5m above the flat part of the track. Where does the particle finally come to rest?
 View Solution
View SolutionA particle of mass m and speed u collides elastically with the end of a uniform rod of mass M and length L as shown. If the particle comes to rest after collision, find mM
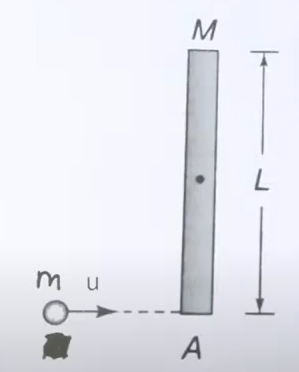 View Solution
View SolutionA particle of mass 5kg is free to slide on a smooth ring of radius r=20cm fixed in a vertical plane. The particle is attached to one end of a spring whose other end is fixed to the top point O of the ring. Initially, the particle is at rest at a point A of the ring such that ∠OCA=60∘, C being the centre of the ring. The natural length of the spring is also equal to r=20cm. After the particle is released and slides down the ring, the contact force between the particle and the ring becomes zero when it reaches the lowest position B. Determine the force constant (in×102Nm−1) of the spring.
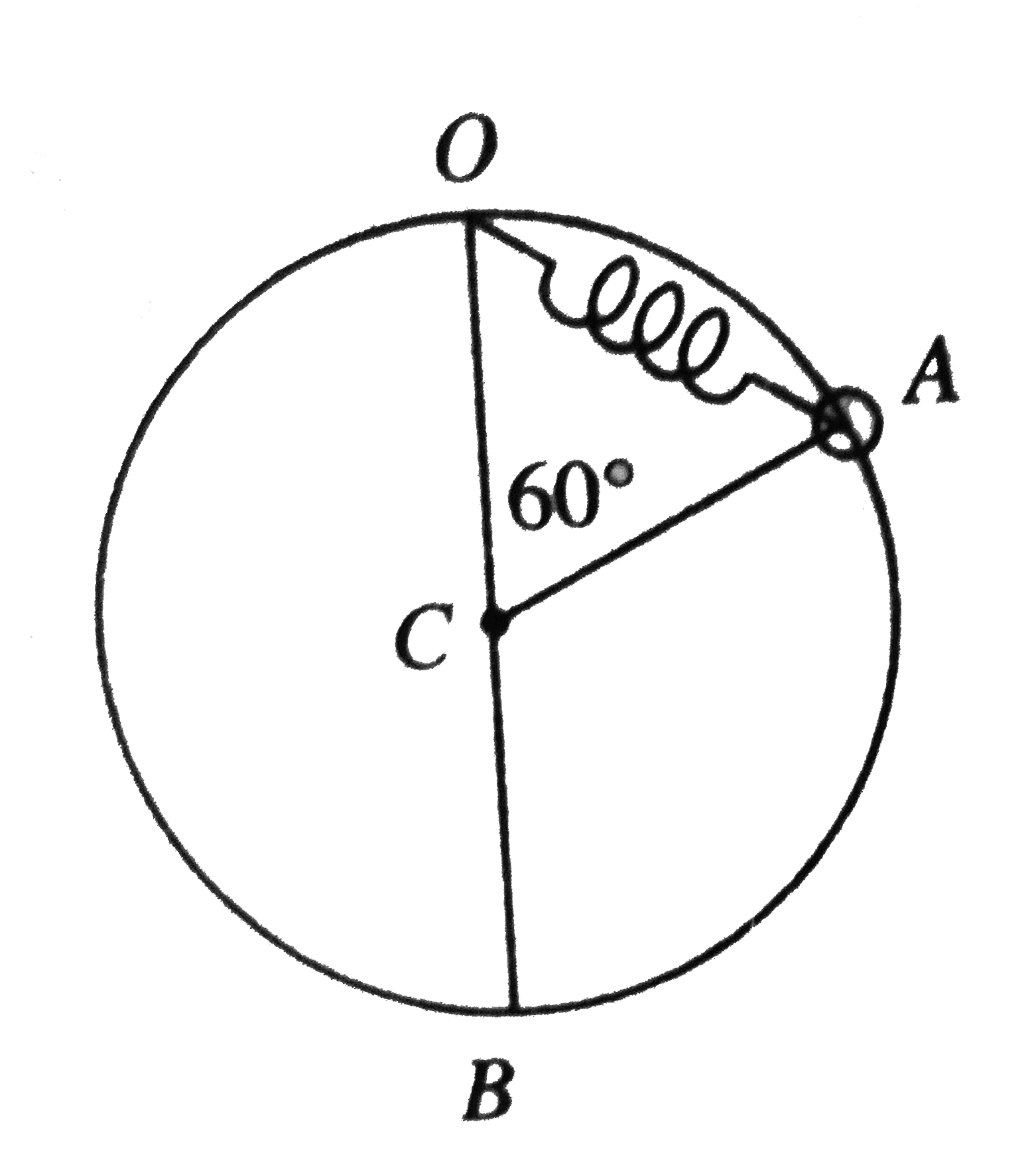 View Solution
View SolutionA particle of mass m is pulled along an arbitrary curved surface without acceleration as shown in figure. Coefficient of friction between surface and particle is μ. Then

codes:View Solution

