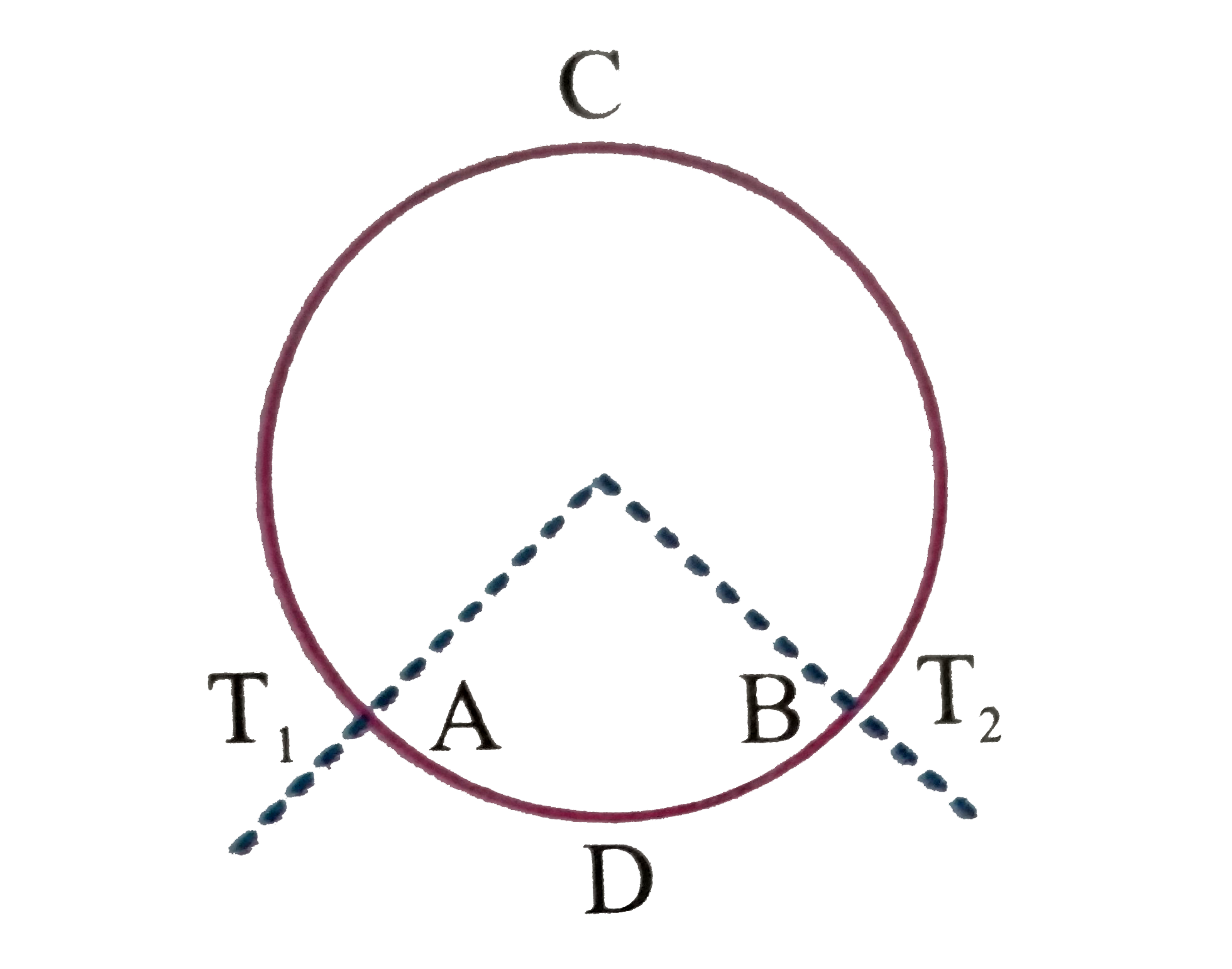
A ring consisting of two parts ADB and ACB of same conductivity k carries an amount of heat H The ADB part is now replaced with another metal keeping the temperature T1) and T2 constant The heat carried increases to 2H What should be the conductivity of the new ADB Given ACBADB=3
 .
.
73K
2k
52K
3K
The correct Answer is:A
Heat carried increases to 2 times. Therefore, new net thermal resistance will remain half.
∴ R′=R2⇒R′1R′2R′1+R′2=R1R22(R1+R2)
or (3l/KA)(l/K′A)(3l/KA)+(l/K′A)=(3l/KA)(l/KA)2{3lKA+lKA}
Solving, this we get K′=73K
Topper's Solved these Questions
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Assertion and reason
17 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Match the columns
4 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Check points 16.4
29 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 Subjective
14 Videos
- CENTRE OF MASSBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
Similar Questions
Consider two rods of same length and different specific heats (S1 and S2), conductivities K1 and K2 and area of cross section (A1 and A2) and both having temperature T1 and T2 at their ends. If the rate of heat loss due to conduction is equal then
View SolutionA rod of length l and cross sectional area A has a variable conductivity given by K=αT, where α is a positive constant T is temperatures in Kelvin. Two ends of the rod are maintained at temperatures T1 and T2(T1>T2). Heat current flowing through the rod will be
View Solution
Knowledge Check
The temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thickness x and 4x respectively. Temperatures on the opposite faces of composite slab are T1andT2 where T2>T1, as shown in fig. what is the rate of flow of heat through the slab in a steady state?
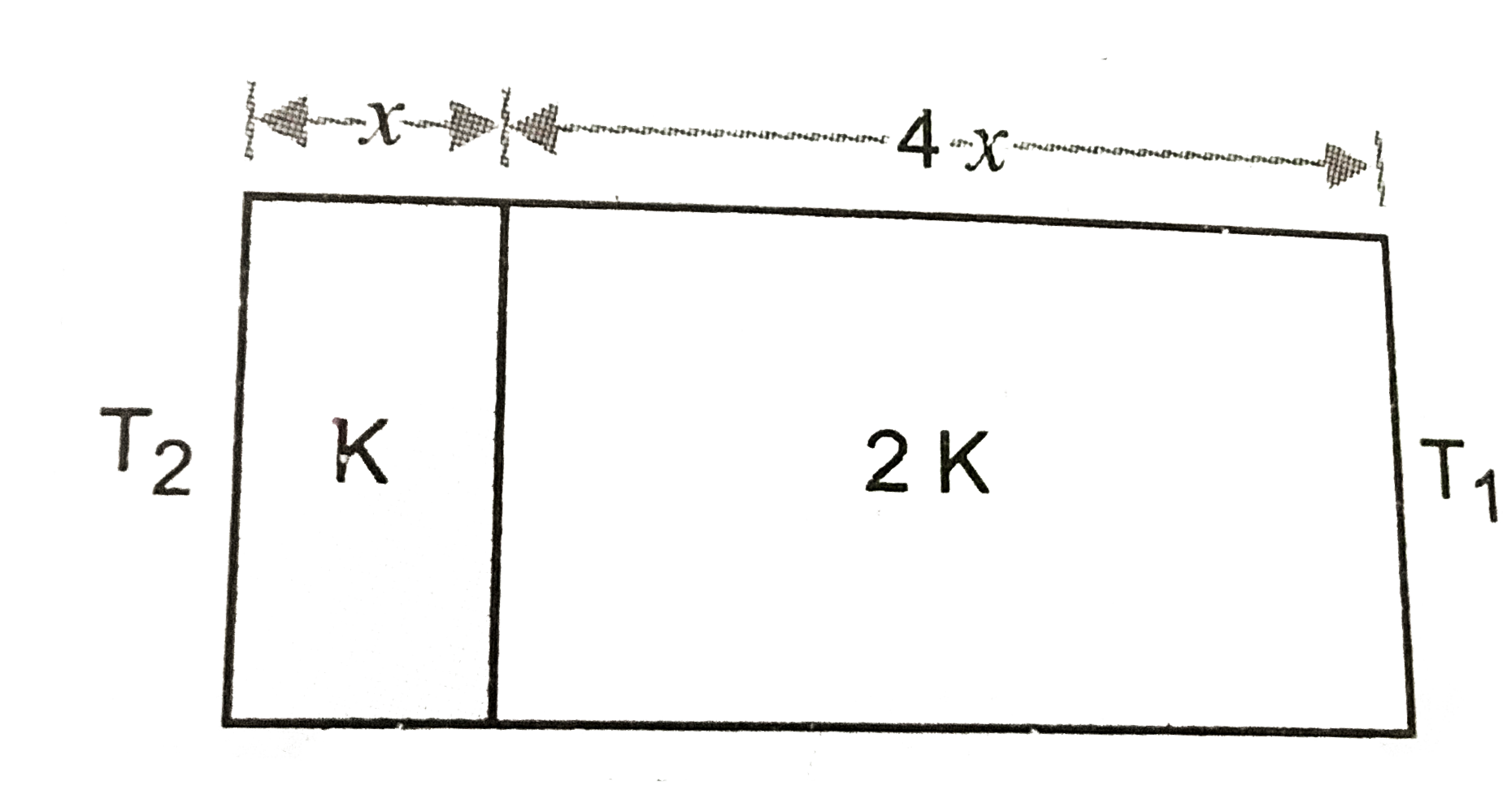 A1B12C23D13
A1B12C23D13
A rod of length l with thermally insulated lateral surface consists of material whose heat conductivity coefficient varies with temperature as k=a/T, where a is a constant. The ends of the rod are kept at temperatures T1andT2. Find the function T(x), where x is the distance from the end whose temperature is T1.
View SolutionA rod of length l and cross-section area A has a variable thermal conductivity given by K = α T, where α is a positive constant and T is temperature in kelvin. Two ends of the rod are maintained at temperature T1 and T2 (T1>T2). Heat current flowing through the rod will be
View SolutionTwo metal rods 1 and 2 of same lengths have same temperature difference between their ends. Their thermal conductivities are K1 and K2 and cross sectional areas A1 and A2 respectively. If the rate of heat conduction in 1 is four times that in 2, then
View SolutionFour identical rods AB,CD,CFandDE are joined as shown in figure. The length, cross-sectional area and thermal conductivity of each rod are l,AandK respectively. The ends A,EandF are maintained at temperature T1 , T2 and T3 respectively. Assuming no loss of heat to the atmosphere, find the temperature at B.

View SolutionA cylindrical block of length 0.4 m and area of cross-section 0.04m2 is placed coaxially on a thin metal disc of mass 0.4 kg and of the same cross - section. The upper face of the cylinder is maintained at a constant temperature of 400 K and the initial temperature of the disc is 300K. if the thermal conductivity of the material of the cylinder is 10watt/m−K and the specific heat of the material of the disc is 600J/kg−K, how long will it take for the temperature of the disc to increase to 350 K? Assume for purpose of calculation the thermal conductivity of the disc to be very high and the system to be thermally insulated except for the upper face of the cylinder.
View SolutionThree rods of same cross-section but different length and conductivity are joined in series . If the temperature of the two extreme ends are T1andT2(T1>T2) find the rate of heat transfer H.

View SolutionTwo conducting cylinders of equal length but different radii are connected in series between two heat baths kept at temperatures T1=300KandT2=100K, as shown in the figure. The radius of the bigger cylinder is twice that of the smaller one and the thermal conductivities of the materials of the smaller and the larger cylinders are K1andK2 respectively. If the temperature at the junction of the two cylinders in the steady state is 200 K, then K1/K2=__________.
View Solution
