Two metal rods 1 and 2 of same lengths have same temperature difference between their ends. Their thermal conductivities are K1 and K2 and cross sectional areas A1 and A2 respectively. If the rate of heat conduction in 1 is four times that in 2, then
K1A1=K2A2
K1A1=4K2A2
K1A1=2K2A2
4K1A1=K2A2
To solve the problem, we need to use the formula for the rate of heat conduction through a rod, which is given by Fourier's law of heat conduction:
dqdt=K⋅A⋅ΔTL
Where:
- dqdt is the rate of heat transfer,
- K is the thermal conductivity of the material,
- A is the cross-sectional area,
- ΔT is the temperature difference across the rod,
- L is the length of the rod.
1. Identify the Given Information:
- Rod 1 has thermal conductivity K1, cross-sectional area A1, and length L.
- Rod 2 has thermal conductivity K2, cross-sectional area A2, and length L.
- The temperature difference across both rods is the same: ΔT1=ΔT2=ΔT.
- The rate of heat conduction in rod 1 is four times that in rod 2:
dq1dt=4⋅dq2dt
2. Write the Heat Conduction Equations:
For rod 1:
dq1dt=K1⋅A1⋅ΔTL
For rod 2:
dq2dt=K2⋅A2⋅ΔTL
3. Set Up the Equation Based on Given Condition:
According to the problem:
K1⋅A1⋅ΔTL=4⋅K2⋅A2⋅ΔTL
4. Cancel Common Terms:
Since ΔT and L are the same for both rods, we can cancel them out:
K1⋅A1=4⋅K2⋅A2
5. Rearranging the Equation:
This can be rearranged to find the relationship between the thermal conductivities and areas:
K1K2=4⋅A2A1
Conclusion:
The relationship derived from the problem is:
K1⋅A1=4⋅K2⋅A2
- dqdt is the rate of heat transfer,
- K is the thermal conductivity of the material,
- A is the cross-sectional area,
- ΔT is the temperature difference across the rod,
- L is the length of the rod.
- Rod 1 has thermal conductivity K1, cross-sectional area A1, and length L.
- Rod 2 has thermal conductivity K2, cross-sectional area A2, and length L.
- The temperature difference across both rods is the same: ΔT1=ΔT2=ΔT.
- The rate of heat conduction in rod 1 is four times that in rod 2:
dq1dt=4⋅dq2dt
For rod 1:
dq1dt=K1⋅A1⋅ΔTL
For rod 2:
dq2dt=K2⋅A2⋅ΔTL
According to the problem:
K1⋅A1⋅ΔTL=4⋅K2⋅A2⋅ΔTL
Since ΔT and L are the same for both rods, we can cancel them out:
K1⋅A1=4⋅K2⋅A2
This can be rearranged to find the relationship between the thermal conductivities and areas:
K1K2=4⋅A2A1
The relationship derived from the problem is:
K1⋅A1=4⋅K2⋅A2
Similar Questions
Two metal rods 1 and 2 of the same length have same temperature difference between their ends. Their thermal conductivities are K1andK2 and cross-section areas A1andA2 respectively. What is the required condition for the same rate of heat conduction in them?
View SolutionTwo rods P and Q of equal lengths have thermal conductivities K1andK2 and cross-sectional areas A1andA2 respectively. If the temperature difference across the ends of each rod is the same, then the condition for which the rate of flow of heat through each of them will be equal, is
View SolutionConsider two rods of same length and different specific heats (S1 and S2), conductivities K1 and K2 and area of cross section (A1 and A2) and both having temperature T1 and T2 at their ends. If the rate of heat loss due to conduction is equal then
View SolutionTwo rods A and B of different materials are welded together as shown in figure. Their thermal conductivities are K1 and K2. The thermal conductivity of the composite rod will be

View SolutionCondider two rods of same length and different specific heats (s1,s2), thermal conductivities (K1,K2) and areas of cross-section (A1,A2) and both having temperatures (T1,T2) at their ends. If their rate of loss of heat due to conduction are equal, then
View SolutionTwo rods A and B are of equal lengths. Their ends of kept between the same temperature and their area of cross-section are A1 and A2 and thermal conductivities K1 and K2. The rate of heat transmission in the two rods will be equal, if
View SolutionTwo rods of same length and areas of cross section A1 and A2 have their ends at same temperature. If K1 and K2 are their thermal conductivities, C1 and C2 their specific heats and ρ1 and ρ2 are their densities, then the condition that rate of flow of heat is same in both the rods is
View SolutionTwo identical rods are made of different materials whose thermal conductivities are K1andK2. They are placed end to end between two heat reservoirs at temperatures θ1andθ2. The temperature of the junction of the rod is

View SolutionSteady state temperature are shown in the diagram. Find ratio of thermal conductivity k1k2 if length of all rods are same

View SolutionThree rods A, B and C of the same length and same cross-sectional area are joined as shown. Their thermal conductivities are in the ratio 1:2:3/2. If the open ends of A and C are at 200∘C and 18∘C, respectively, then the temperature at the junction of A at steady state is
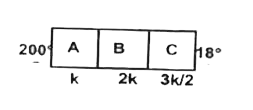
View Solution
