A ring of radius $R$ having uniformly distributed charge $Q$ . is mounted on a rod suspended by two identical strings. The tension in strings in equilibrium is $T_{0}$ . Now, a vertical magnetic field is switched on and ring is rotated at constant angular velocity co. Find the maximum value of co h which the ring can be rotated if the strings can withstand a maximum tension of $\frac{3 T_{0}}{2}$

Video Solution

Text Solution

Verified by Experts

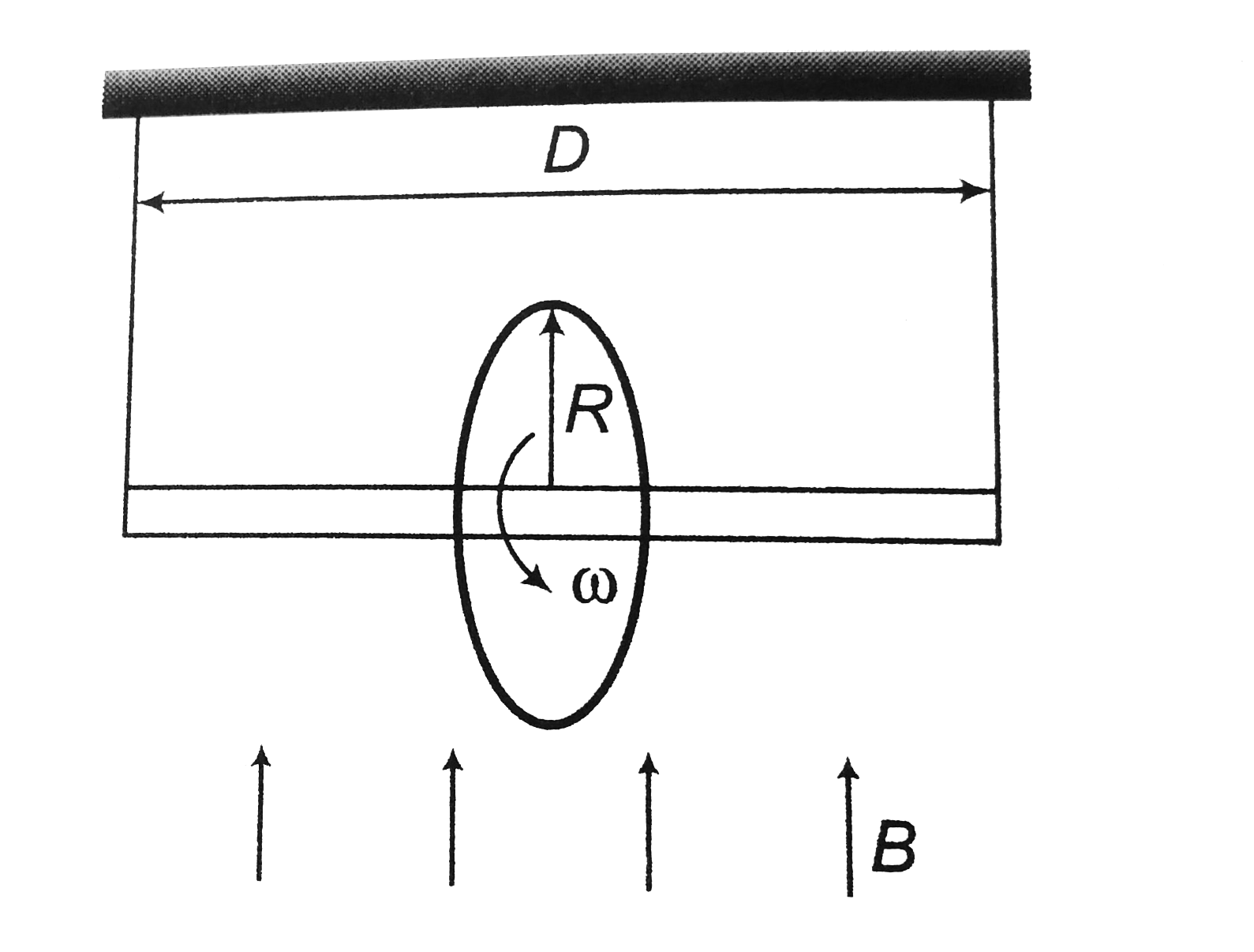
In equilibrium,
$2 T_{0} = m g$
or $T_{0} = \frac{m g}{2} \dots . (i)$
magnetic moment, $M = i A = (\frac{ω}{2 π} Q) (π R^{2})$
$τ = M B {sin 90}^{\circ} = \frac{ω B Q R^{2}}{2}$
Let $T_{1} and T_{2}$ be the tensions in the two strings when magnetic
field is switched on $(T_{1} > T_{2})$
For translation equilibrium,
$T_{1} + T_{2} = m g ... . (i i)$
For rotational equilibrium
$(T_{1} - T_{2}) \frac{D}{2} = τ = \frac{ω B Q R^{2}}{2}$
or $T_{1} - T_{2} = \frac{ω B Q R^{2}}{D} ... . (i i i)$
Solving Eqs. (ii) and (iii) we have
$T_{1} = \frac{m g}{2} + \frac{ω B Q R^{2}}{2 D}$
As $T_{1} > T_{2}$ and maximum values of $T_{1}$ can be $3 T_{0} / 2$ , we have
$\frac{3 T_{0}}{2} = T_{0} + \frac{ω_{max} B Q R^{2}}{2 D} (\frac{m g}{2} = T_{0})$
$∴ ω_{max} = \frac{D T_{0}}{B Q R^{2}}$

|

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

CENGAGE PHYSICS ENGLISH-MAGNETIC FIELD AND MAGNETIC FORCES-Solved Example

Home
Ask Doubt
Profile