A non - conducting ring of mass m = 4 kg and radius R = 10 cm has charge Q = 2 C uniformly distributed over its circumference. The ring is placed on a rough horizontal surface such that the plane of the ring is parallel to the surface. A vertical magnetic field B=4t3T is switched on at t = 0. At t = 5 s ring starts to rotate about the vertical axis through the centre. The coefficient of friction between the ring and the surface is found to be k24. Then the value of k is
The correct Answer is:18
To solve the problem, we will follow these steps:
Step 1: Calculate the Magnetic Flux (Φ)
The magnetic field is given as B=4t3T. The area A of the ring is given by:
A=πR2
where R=0.1m (10 cm converted to meters). Thus,
A=π(0.1)2=π(0.01)=0.01πm2
The magnetic flux Φ through the ring is:
Φ=B⋅A=(4t3)⋅(0.01π)=0.04πt3
Step 2: Calculate the EMF (Electromotive Force)
Using Faraday's law of electromagnetic induction, the EMF E induced in the ring is given by:
E=−dΦdt
Calculating the derivative:
E=−ddt(0.04πt3)=−0.12πt2
Step 3: Calculate the EMF at t=5s
Substituting t=5:
E=−0.12π(52)=−0.12π(25)=−3πV
Step 4: Calculate the Force on the Ring
The force F acting on the ring due to the electric field generated by the EMF is:
F=Q⋅E
where Q=2C:
F=2⋅(3π)=6πN
Step 5: Relate the Force to Friction
The frictional force Ff that prevents the ring from sliding is given by:
Ff=μmg
where m=4kg and g=10m/s2:
Ff=μ(4)(10)=40μ
Step 6: Set the Forces Equal
At the moment the ring starts to rotate, the force due to the EMF equals the frictional force:
6π=40μ
Thus,
μ=6π40=3π20
Step 7: Relate Coefficient of Friction to k
We know from the problem statement that:
μ=k24
Setting the two expressions for μ equal gives:
3π20=k24
Step 8: Solve for k
Cross-multiplying to solve for k:
3π⋅24=20k
k=72π20=18π5
Step 9: Approximate k
Using π≈3.14:
k≈18⋅3.145≈56.525≈11.30
Conclusion
The value of k is approximately 11.30.
The magnetic field is given as B=4t3T. The area A of the ring is given by:
A=πR2
where R=0.1m (10 cm converted to meters). Thus,
A=π(0.1)2=π(0.01)=0.01πm2
Φ=B⋅A=(4t3)⋅(0.01π)=0.04πt3
Using Faraday's law of electromagnetic induction, the EMF E induced in the ring is given by:
E=−dΦdt
Calculating the derivative:
E=−ddt(0.04πt3)=−0.12πt2
Substituting t=5:
E=−0.12π(52)=−0.12π(25)=−3πV
The force F acting on the ring due to the electric field generated by the EMF is:
F=Q⋅E
where Q=2C:
F=2⋅(3π)=6πN
The frictional force Ff that prevents the ring from sliding is given by:
Ff=μmg
where m=4kg and g=10m/s2:
Ff=μ(4)(10)=40μ
At the moment the ring starts to rotate, the force due to the EMF equals the frictional force:
6π=40μ
Thus,
μ=6π40=3π20
We know from the problem statement that:
μ=k24
Setting the two expressions for μ equal gives:
3π20=k24
Cross-multiplying to solve for k:
3π⋅24=20k
k=72π20=18π5
Using π≈3.14:
k≈18⋅3.145≈56.525≈11.30
The value of k is approximately 11.30.
Similar Questions
A non-conducting ring of mass m and radius R has a charge Q uniformly distributed over its circumference. The ring is placed on a rough horizontal surface such that plane of the ring is parallel to the surface. A vertical magnetic field B=B0t2 tesla is switched on. After 2 a from switching on the magnetic field the ring is just about to rotate about vertical axis through its centre.
(a) Find friction coefficient μ between the ring and the surface.
(b) If magnetic field is switched off after 4s, then find the angle rotated by the ring before coming to stop after switching off the magnetic field.
View SolutionA non-conducting ring having q uniformly distributed over its circumference is placed on a rough horizontal surface. A vertical time varying magnetic field B=4t2 is switched on at time t = 0. Mass of the ring is m and radius is R.
The ring starts rotating after 2 s, the coefficient of friction between the ring and the table is
View SolutionA non-conducting ring having q uniformly distributed over its circumference is placed on a rough horizontal surface. A vertical time varying magnetic field B=4t2 is switched on at time t = 0. Mass of the ring is m and radius is R.
The ring starts rotating after 2 s, the coefficient of friction between the ring and the table is
View SolutionA charge q is uniformly distributed over a quarter circular ring of radius r. The magnitude of electric field strength at the centre of the ring will be
View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring.

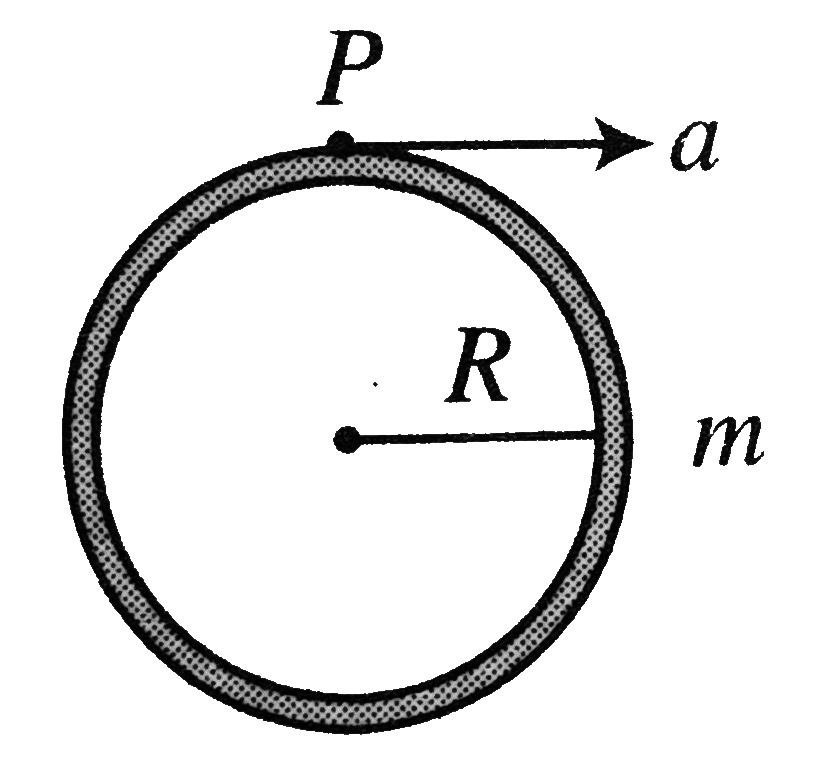
View SolutionA smooth ring of mass m and radius R=1m is pulled at P with a constant acceleration a=4ms−2 on a horizontal surface such that the plane of the ring lies on the surface. Find the angular acceleration of the ring at the given position. (in rad/s2)
View SolutionA ring of mass m, radius r having charge q uniformly distributed over it and free to rotate about its own axis is placed in a region having a magnetic field B parallel to its axis. If the magnetic field is suddenly switched off, the angular velocity acquired by the ring is:
View SolutionA ring of radius 'R' having change 'q' uniformly distributed over it passes through a sphere lies at circumference of ring the centre of ring lies at surface of sphere.Then flux linked with sphere is
View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring .The

View SolutionMass is non - uniformly distributed on the circumference of a ring of radius a and centre at origin . Let b be the distance of centre of mass of the ring from origin. Then ,
View Solution
