A ring of radius R is made from a thin wire of radius r. If is the density of the material of wire then what will be the gravitational force exerted by the ring on the material particle of mass m placed on the axis of ring of ring at a distance x from its centre. Shown that the force will be maximum when and the maximum value of force will be given as
Step by step video & image solution for A ring of radius R is made from a thin wire of radius r. If rho is the density of the material of wire then what will be the gravitational force exerted by the ring on the material particle of mass m placed on the axis of ring of ring at a distance x from its centre. Shown that the force will be maximum when x=R//sqrt(2) and the maximum value of force will be given as F_(max)=(4pi^(2)G r^(2)rhom)/((3)^(3//2)R^(2)) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GRAVITATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Particle Exercise
50 Videos
- GRAVITATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Discussion Qns
31 Videos
- FLUID MECHANICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - FLUID MECHANICSEXERCISE - Unsolved Numerical Problems
86 Videos
- KINEMATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Unsolved Numerical Pro.
83 Videos
Similar Questions
Potential on the axis of ring of radius 3R and at distance 4R from centre of ring is (charge on the ring is Q )
View SolutionA particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View Solution
Knowledge Check
A mass m is placed at point P lies on the axis of a ring of mass M and radius R at a distance R from its centre. The gravitational force on mass M is
AGMm√2R2BGMm2R2CGMm2√2R2DGMm4R2Consider a ring of mass m and radius r. Maximum gravitational intensity on the axis of the ring has value.
AGmr2B2Gm√3r2C2Gm3√3r2DGm2r2For a uniform ring of mass M and radius R at its centre
Afield and potential both are zeroBfield is zero but potential is GMRCfield is zero but potential is −GM/RDmagnitude of field is GMR2 and potential −GMR
Find the force of attraction on a particle of mass m placed at the centre of a quarter ring of mass mand radius R as shown in figure.
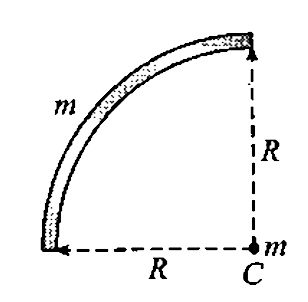
View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .

View SolutionFind the intensity of gravitational field at a point lying at a distance x from the centre on the axis of a ring of radius a and mass M.
View SolutionA thin wire ring of radius r has an electric charge q. What is the tension of the wire if a point charge q0 is placed at the ring's centre?
View SolutionA ring of radius R has charge −Q distributed uniformly over it. Calculate the charge that should be placed at the center of the ring such that the electric field becomes zero at apoint on the axis of the ring at distant R from the center of the ring.
View Solution
