A river 600m wide wide flows at the rate of 8 km h^(-1). Still water, wishes to cross the river straight (i) Along what direction must be strike ? What will be his resultant velcity ? (ii) How much time he will take to cross the river ?
Refer to fig, 2 9c ) . 49,
 .
.
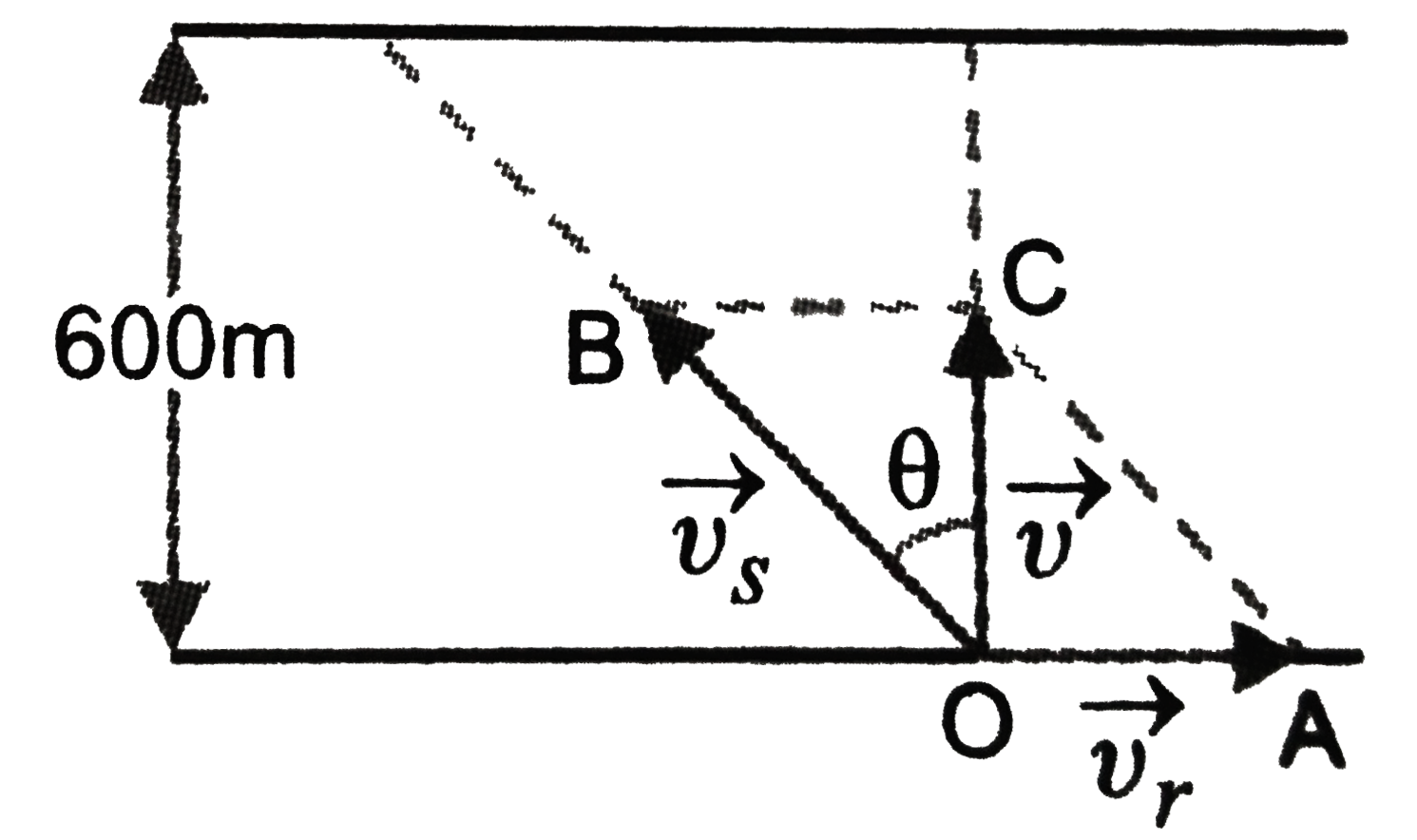
velocity of river, | vec v-r| = |vec (OP)| = 8 km h^(-1)<br>velocityofswimmer∈stillwater,<br> | vec v_s | = | vec (OB) | = 10 km h^-1)<br>9i0Theswimmerwillcrosstheriverstraightiftherestant–––––velocity vec vofvelocityofriverandvelcotyofswimmer vec _sactsalong vec (OP),i.e.,perpendica––r→thebankofricer.Itwillbesoittheswimmermocesalong vec (OB)where /_BOC= theta.Inright∠d△ OBC<br> sin theta = (BC)/(OB) = v_r/ v_s = 8/ (18) = 0.8= sin 53 ^@ 8'<br>or theta = 53^@ 8'<br>Therefore,the∠atwhichtheswimmeris→swim = 90^@ + 53^@ 8' = 143^@ 8'withtheriverstream.<br>(ii)Restant–––––velocityofatswimmer<br> v= sqrt(v_s^2-v_e^2) =sqrt 910^2 -8^2 )= 6 km h^(-1)<br>= 5/3 ms^(-1)<br>(iii)Timetaken→crosstheriver,<br> t =(width of ricer 0/v = (600 m) /(5//3 ms^(-1)) = 36 0 s = 6 min.
Topper's Solved these Questions
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 4 SolvedExamples
31 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 Conceptual Problems
2 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 2 SolvedExamples
31 Videos
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - Assertion-Reason Type Questions
19 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Assertion- Reason Type Questions
17 Videos
Similar Questions
A river 800m wide flows at the rate of 6kmh_1 in still water, wishes to cross the tiver straight. ltbRgt (a) Along what direction must he strike ?
(b) What should be his resultant velocity ?
(c ) How much time he would take ?
View SolutionA river 800 m wide flows at the rate of 5kmh−1. A swimmer who can swim at 10kmh−1 in still water, wishes to cross the river straight. (i) Along what direction must be strike ? (ii) What should be his resultant velocity ? (iii) How much time he would take ?
View Solution
Knowledge Check
A river 3 m deep and 60 m wide is flowing at the rate of 2.4 km/h . The amount of water running into the sea per minute is :
A6000m3B6400m3C6800m3D7200m3
A river 500m wide flows at a rate at a rate of 4kmh−1. A swimmer who can swim at 8kmh−1. In still water, wishes to cross the river straight. (i) Along what direction must he strike? (ii) What should be his resultant velocity. (iii) What is the time of crossing the river?
View SolutionA man can swim at the rate of 5kmh−1 in still water. A 1−km wide river flows at the rate of 3kmh−1 The man wishes to swim across the river directly opposite to the starting point.
(a) Along what direction must the man swim ?
(b) What should be his resultant velocity ?
( c) How much time will he take to cross the river ?
View SolutionA man can swim at the rate of 5kmh−1 in still water A. One km wide river flows at the rate of 3kmh−1 . The man wishes to swim across the river directly opposite to the starting point. How much time will be take to cross the river
View SolutionA man can swim at the rate of 5kmh−1 in still water A. One km wide river flows at the rate of 3kmh−1 . The man wishes to swim across the river directly opposite to the starting point. How much time will be take to cross the river
View SolutionA river is flowing steradily with a speed 5kmh−1 . A boat man can row with a speed of 10kmh−1 in still water. He rows his boat in river at right angles to the bank of river, If width of river is 800m, (i) how much time the boat man will take to cross the river ? (ii) How far away from a point just opposite to the bank of river he will be reaching there ? (ii) What will be his effective speed gt
View SolutionA rever 500m wide flows at a rate at a rate of 4kmh−1. A swinmmer who can swin at 8kmh−1. In still water, wishes to cross the river straight . (i) Along what direection must he strike? (ii) What should be his resultant velocity. (ii) What is the time of crossing the river?
View SolutionA river is 12km wide and flows at the rate of 3 kmph. A man, who can swim in still water at the rate of 5 kmph wishes to reach the other bank of the river. In what direction should he start swimmin to cross the river (a) along the shortest route, (b) in the shortest possible time ? Calculate how much time he will take to cross the river in the two cases.
View Solution
