Derermine the horizontal force required to displace a mass of 0.03kg suspended by a string until the string makes an angle 300 with the vertical.
To determine the horizontal force required to displace a mass of 0.03 kg suspended by a string until the string makes an angle of 30 degrees with the vertical, we can follow these steps:
Step 1: Understand the Forces Acting on the Mass
When the mass is displaced, it is in equilibrium under the influence of three forces:
1. The tension (T) in the string.
2. The weight (mg) of the mass acting downwards.
3. The horizontal force (F) acting to displace the mass.
Step 2: Resolve the Tension into Components
The tension in the string can be resolved into two components:
- A vertical component: Tcos(30∘)
- A horizontal component: Tsin(30∘)
Step 3: Apply the Equilibrium Condition
In the vertical direction, the forces must balance:
Tcos(30∘)=mg
Where:
- m=0.03kg
- g=10m/s2 (approximately)
Step 4: Calculate the Tension (T)
From the equilibrium condition:
T=mgcos(30∘)
Substituting the values:
T=0.03×10cos(30∘)
Step 5: Calculate cos(30∘)
We know:
cos(30∘)=√32
Thus, substituting this in:
T=0.03×10√32=0.3√32=0.6√3
Step 6: Calculate the Horizontal Force (F)
The horizontal force is given by:
F=Tsin(30∘)
And we know:
sin(30∘)=12
Substituting for T:
F=(0.6√3)×12=0.62√3=0.3√3
Step 7: Simplify the Expression
To express F in numerical form:
F=0.3√3
Using √3≈1.732:
F≈0.31.732≈0.173N
Final Answer
Thus, the horizontal force required to displace the mass is approximately:
F≈0.173N
---
When the mass is displaced, it is in equilibrium under the influence of three forces:
1. The tension (T) in the string.
2. The weight (mg) of the mass acting downwards.
3. The horizontal force (F) acting to displace the mass.
The tension in the string can be resolved into two components:
- A vertical component: Tcos(30∘)
- A horizontal component: Tsin(30∘)
In the vertical direction, the forces must balance:
Tcos(30∘)=mg
Where:
- m=0.03kg
- g=10m/s2 (approximately)
From the equilibrium condition:
T=mgcos(30∘)
Substituting the values:
T=0.03×10cos(30∘)
We know:
cos(30∘)=√32
Thus, substituting this in:
T=0.03×10√32=0.3√32=0.6√3
The horizontal force is given by:
F=Tsin(30∘)
And we know:
sin(30∘)=12
Substituting for T:
F=(0.6√3)×12=0.62√3=0.3√3
To express F in numerical form:
F=0.3√3
Using √3≈1.732:
F≈0.31.732≈0.173N
Thus, the horizontal force required to displace the mass is approximately:
F≈0.173N
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 4 SolvedExamples31videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 Conceptual Problems2videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 2 SolvedExamples31videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - Assertion-Reason Type Questions19videos
GRAVIATION
- BOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Assertion- Reason Type Questions17videos
LAWS OF MOTION
Similar Questions
A stone of mass 2kg whirled in a horizontal circle attached at the end of 1.5 m long string. If the string makes an angle of 30∘ with vertical, compute its period (g=9.8m/s2) .
View SolutionA stone of mass 1 kg is whirled in horizontal circle attached at the end of a 1 m long string. If the string makes an angle of 30∘ with vertical, calculate the centripetal force acting on the stone. (g=9.8 m/s2).
View Solution
Knowledge Check
- Question 1 - Select One
A mass of M kg is suspended by a weightless string. The horizontal force that is required to displace it until the string makes an angle 45∘ with the initial vertical direction is
AMgBMg√2CMg(√2+1)D√2Mg - Question 2 - Select One
A mass of M kg is suspended by a weightless string. The horizontal force that is required to displace it until the string makes an angle of 45∘ with the initial vertical direction is
AMg(√2+1)BMg√2CMg√2DMg(√2−1) - Question 3 - Select One
A mass of M kg is suspended by a weightless string. The horizontal force that is required to displace it until the string makes an angle of 45∘ with the initial vertical direction is
AMg(√2+1)BMg√2CMg√2DMg(√2−1)
A mass of M kg is suspended by a weightless string. The horizontal force that is required to displace it until the string makes an angle of 45∘ with the initial vertical direction is
View SolutionA mass of M kg is suspended by a weightless string. The horizontal force required to displace it until string makes an angle of 45∘ with the initial vertical direction is:
View SolutionA heavy particle of mass 1kg suspended from a massless string attached to a roof. A horizontal force F is applied to the particle such that in the equilibrium position the string makes and angle 30∘ with the vertical. The magnitude of the force F equals
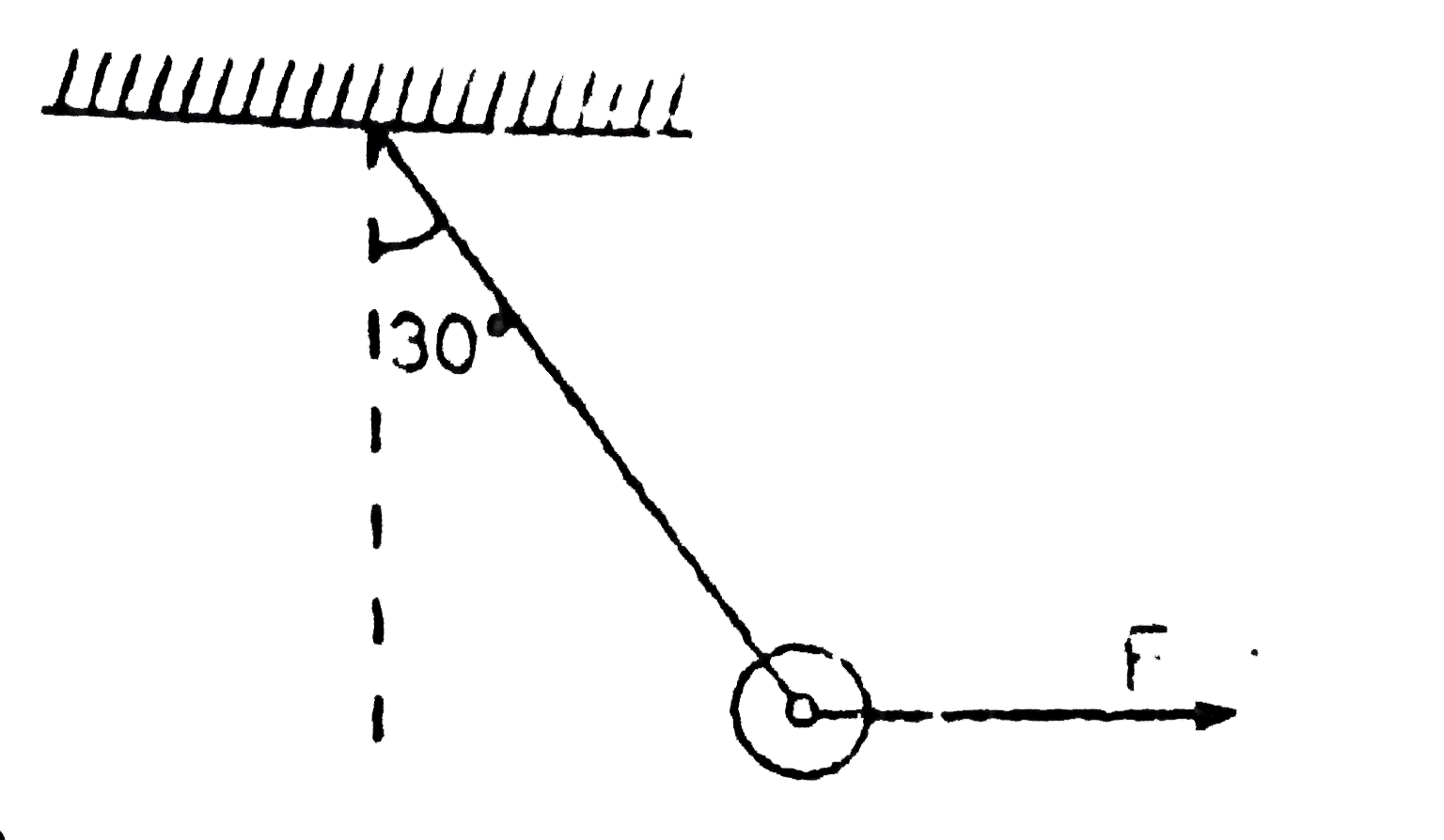 .View Solution
.View SolutionA body of mass √3 kg is suspended by a string to rigid support.The body is pulled horizontally by a force F until the string makes an angle of 30∘ with the vertical.The value of F and tension in the string are
View SolutionA 10 kg block is at rest as shown on a horizontal surface having a coefficient of static friction of 0.7 String -1 is horizontal and string-2 makes an angle of 30∘ with the verticle. A mass M hangs from String- 3. Which of the following statement(S) about this situation is //are ? (g=10m/s2)
 View Solution
View Solution

