A rocket accelerates straight up by ejecting gas downwards. In a small time interval , it ejects a gas of mass at a relative speed . Calculate KE of the entire system at and and show that the device that ejects gas does work in this time interval (neglect gavity).
Let be the mass of rocket at any time t and
the velocity of rocket at this time
mass of gas ejected in time interval with relative vel. .
At time (KE) and At time of rocket KE of gas
Expanding and neglecting terms which are too small, we get
...(i)
As
From (i), using work energy theorem.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Advanced Problems For Competitions
20 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - NCERT EXERCISES WITH SOLUTIONS
30 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Short Answer Question
52 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions
19 Videos
Similar Questions
A uniform rod of length L and mass M, is lying on a frictionless horizontal plane and is pivoted at one of its ends, as shown in the figure. An inelastic ball of mass m is fixed with the rod at a distance L/3 from O. A horizontal impulse J is given to the rod at a distance 2L/3 from O in a direction perpendicular to the rod. Assume that the ball remains in contact with the rod after the collision and the impulse J acts for a small time interval Δt.
(a) Find with resulting instantaneous angular velocity of the rod just after the impusle is imparted.
(b) Find the impulse acted on the ball during the time interval Δt.
(c ) Find the magnitude and direction of the impulse applied by the pivot during the time interval Δt.

View SolutionA body is thrown up in a lift with a velocity u relative to the lift, and returns to the lift in time t. Show that the liftsupwardae≤rationis(2u-gt)/(t).
View Solution
Knowledge Check
Suppose a rocket with an intial mass M0 eject a mass Δm in the form of gases in time Δt, then the mass of the rocket after time t is :-
AM0−ΔmΔt.tBM0−ΔmΔtCM0−ΔmΔtDM0In U.C.M., when time interval δt→0 , the angle between change in velocity (δv) and linear velocity ( v) will be
A0∘B90∘C180∘D45∘Each of the three graphs represents acceleration versus time for an object that already has a positive velocity at time t1. Which graphs show an object whose speed is increasing for the entire time interval between t1 and t2?
 Agraph I, onlyBgraphs I and II, onlyCgraphs I and III, onlyDgraphs I, II, and III
Agraph I, onlyBgraphs I and II, onlyCgraphs I and III, onlyDgraphs I, II, and III
A rocket of mass 5700 kg ejects mass at a constant rate of 15 kg/s withe constant speed of 12 km/s. The acceleration of the rocket 1 minute after the blast is (g=10m/s2)
View SolutionA technique called photelectron spectroscopy is used to measure the I.P of atoms. A same is irradiated with U.V light, and electrons are ejected from the valence shell. The kinetic energy of the ejected electrons are measured. Since, the energy of the U.V. photon and the kinetic energy of the ejected electrons are known, we can write
hv=I.P.+12mu2
Where v is the frequency of the U.V light, and m and u are mass and velocity of the electron respectively. In one experiment the kinetic energy of the ejected electron from potassium is found to be. 5.34×10−19J using U.V. source of wavelength 162 nm. Calculate I.E. of potassium (h=6.62×10−34J−s,c=3×108m / s).
View SolutionEach of the three graphs represents acceleration versus time for an object that already has a positive velocity at time t1. Which graphs show an object whose speed is increasing for the entire time interval between t1andt2 ?
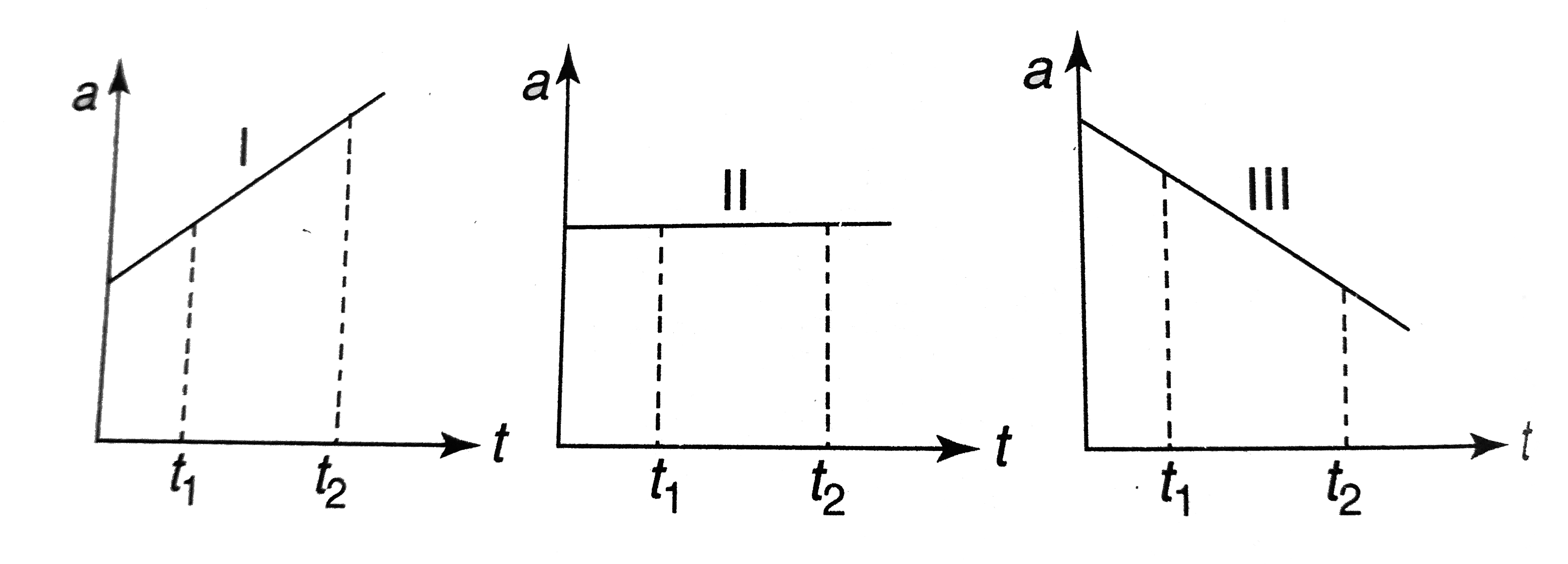
View SolutionA truck moving on a smooth horizotanal surface with a uniform speed u is carrying stonedust . If a mass Δm of the stone-dust 'leaks' from the truck in a timeΔt, the force needed to keep the truck moving at its uniform speed is
View SolutionAn older-model car accelerates from 0 to speed v in a time interval of Δt. A newer, more powerful sports car accelerates from 0→2v in the same time period. Assuming the energy coming from the engine appears only as kinetic energy of the cars. Choose correct statement.
View Solution
