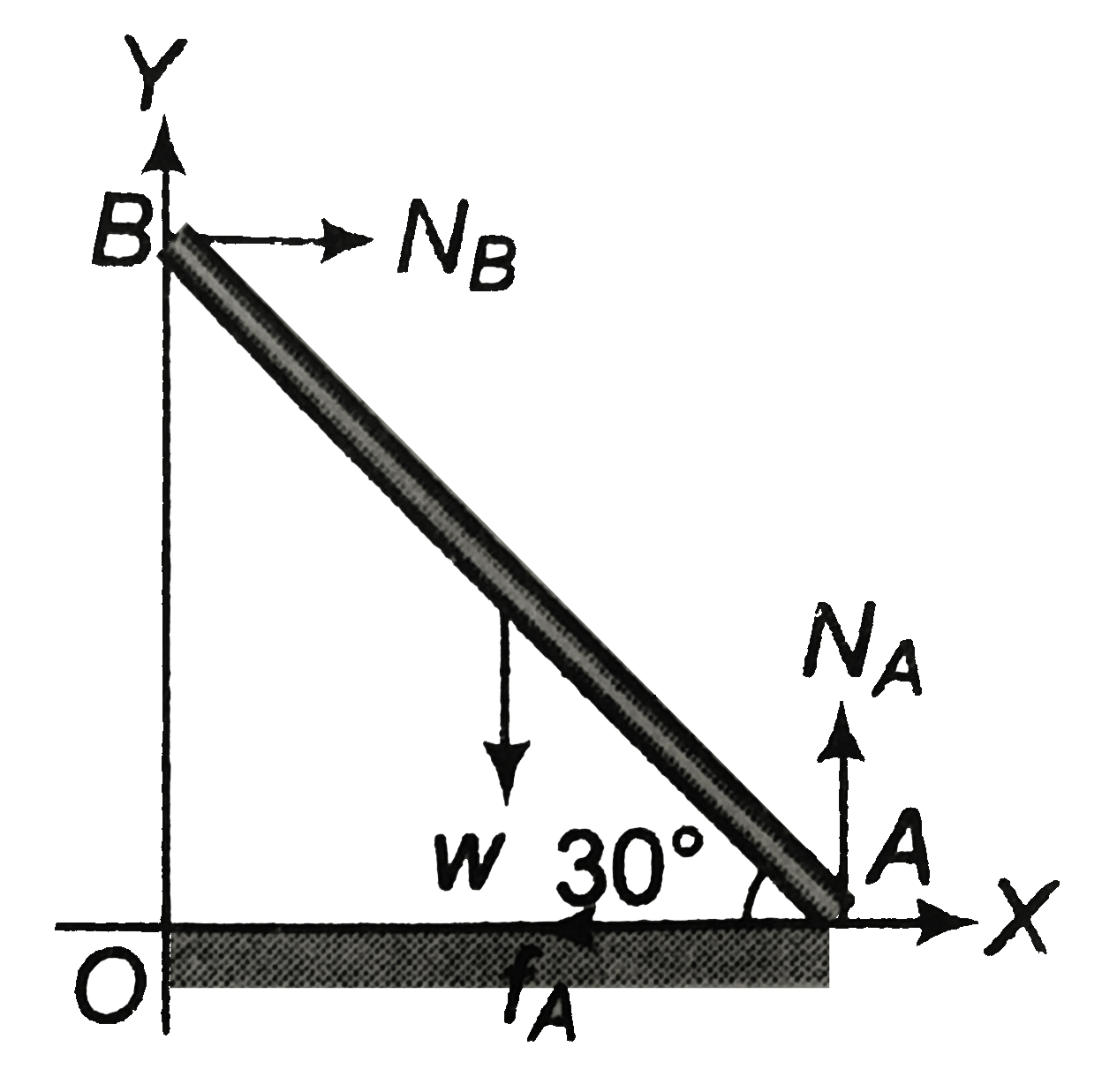
A rod AB rests with the end A on rough horizontal ground and the end B against a smooth vertical wall. The rod is uniform and of weight w. If the rod is in equilibrium in the position shown in figure.Find
(a)frictional shown at A
(b) normal reaction at A
(c) normal reaction at B.

Let length of the rod be 2l. Using the three condition of equibrium. Anticlockwise moment is taken as positive.
(i) ∑Fx=0 ⇒∴ NB−fA=0
or NB=fA …(i)
(ii) ∑Fy=0 ⇒∴ NB−w=0
or NA=w …(ii)
(iii)∑π0=0
:. NA(2lcos30∘)−NB(2lsin30∘)−w(lcos30∘)=0
or √3NA−NB−√32w=0 ...(iii)
Solving these three eqution, we get
fA=√32w (b) NA=w (c) NB=√32w
Similar Questions
A stationary uniform rod of mass 'm', length 'l' leans against a smooth vertical wall making an angle θ with horizontal floor. Find the normal force & frictional force that is exerted by the floor on the rod ?
View SolutionA uniform ladder of mass 10 kg leans against a smooth vertical wall making an angle of 530 with it. The other end rests on a rough horizontal floor. Find the normal force and the frictional force that the floor exerts on the ladder
View Solution
Knowledge Check
A uniform rod AB hinged about a fixed point P is initially vertical. A rod is released from vertical position. When rod is in horizontal position:
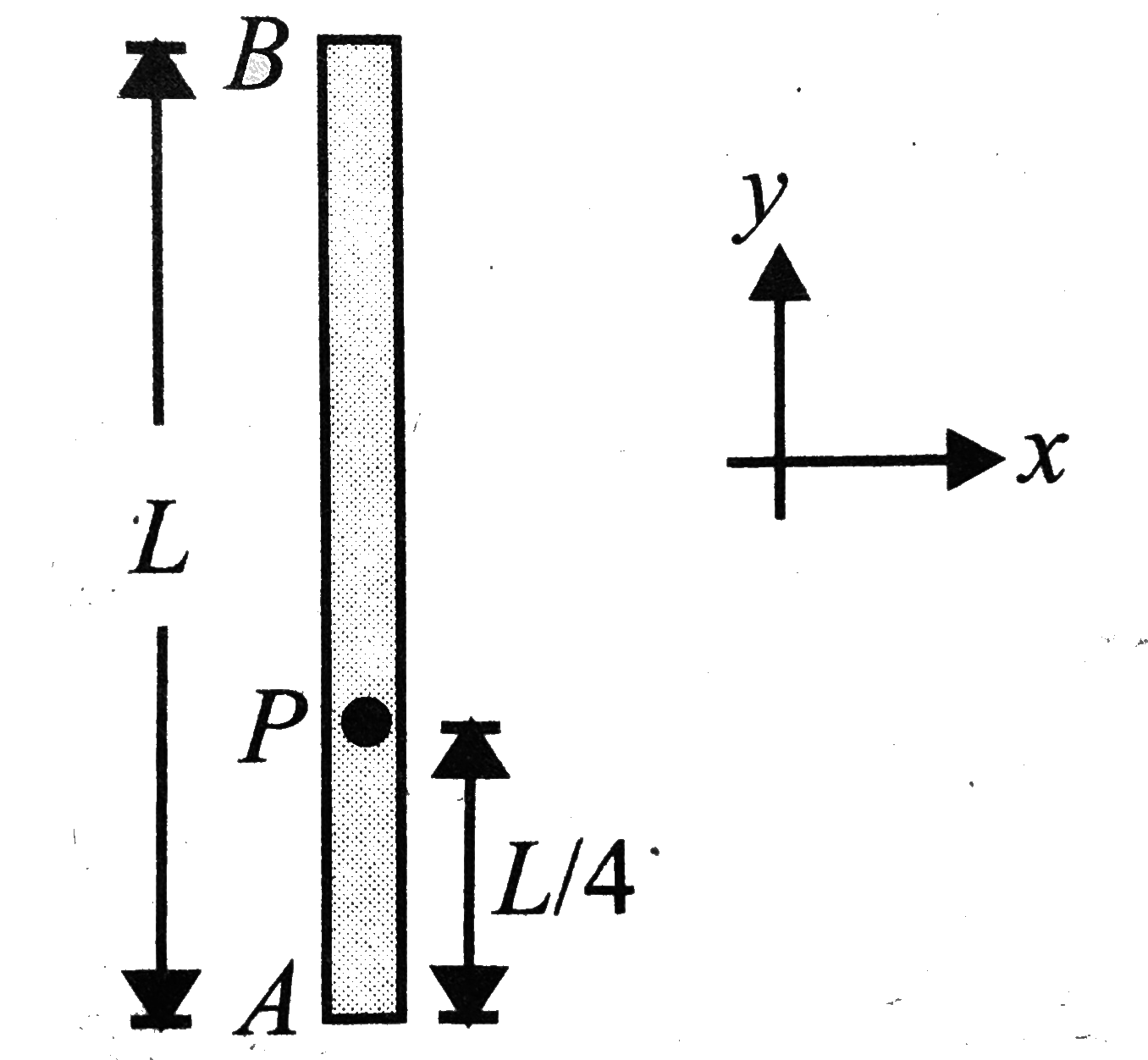
The acceleration of end B of the rod isA−6g7ˆi−12g7ˆjB−5g7ˆi−6g7ˆjC−18g7ˆi−5g7ˆjD−18g7ˆi−9g7ˆjA uniform ladder rests in limiting equilibrium with its lower end on a rough horizontal plane with coefficient of friction μ and its upper end against a smooth vertical wall. If θ is the inclination of the ladder with the wall, then θ is equal to
Atan−1μBcot−1μCcot−1(2μ)Dtan−1(2μ)A uniform ladder rests in limiting equilibrium with its lower end on a rough horizontal plane with coefficient of friction μ and its upper end against a smooth vertical wall. If θ is the inclination of the ladder with the wall, then θ is equal to
Atan−1μBcot−1μCcot−1(2μ)Dtan−1(2μ)
A rod AB of mass M and length L is shown in figure. End A of rod is hinged and end B is lying on the ground. Find the

Normal reaction by ground on the rod
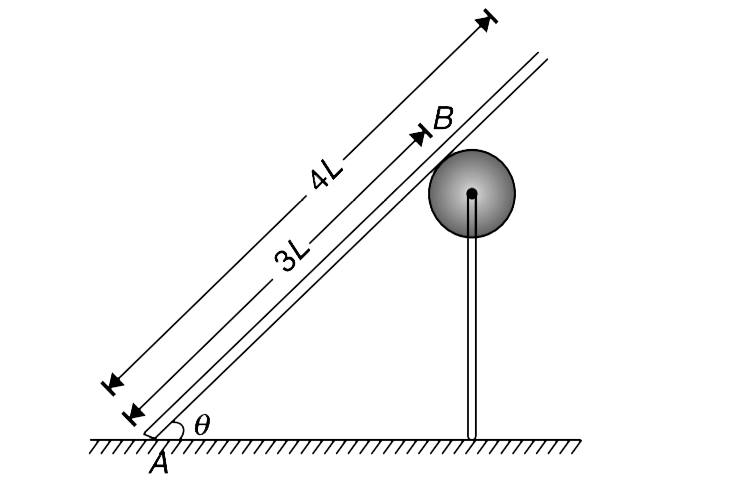
View SolutionA uniform rod has mass M and length 4L. It rests in equilibrium with one end on a rough horizontal surface at A. At point B, at a distance 3L from A, it is supported by a fixed smooth roller. The rod just remains in equilibrium when θ=30∘
(a) Find the normal force applied by the horizontal surface on the rod at point A.
(b) Find the coefficient of friction between the rod and the surface.
View SolutionA uniform beam AB of weight W is standing with the end B on a horizontal floor and end A leaning against a vertical wall. The beam stands in a vertical plane perpendicular to the wall inclined at 45∘ to the vertical, and is in the position of limiting equilibrium. If the two points of contact are equally rough, then the coefficient of friction at each of them is
View SolutionA conducting rod of length l is higed at point O. It is free to rotate in a vertical plane. There exists a uniform magnetic field →B in horizontal direction. The rod is released from the position shown in figure. Potential difference between the two ends of the rod is proportional to
View SolutionA light rod carries three equal masses A, B and C as shown in figure. Find the velocity of B in vertical position of rod, if it is released from horizontal position. As shown in figure.

View Solution
