A rod AB rests with the end A on rough horizontal ground and the end B against a smooth vertical wall. The rod is uniform and of weight w. If the rod is in equilibrium in the position shown in figure.Find
(a)frictional force shown at A
(b) normal reaction at A
(c) normal reaction at B.

Let length of the rod is 2l. Using the three conditions of equilibrium. Anti- clockwise moment is taken as positive.
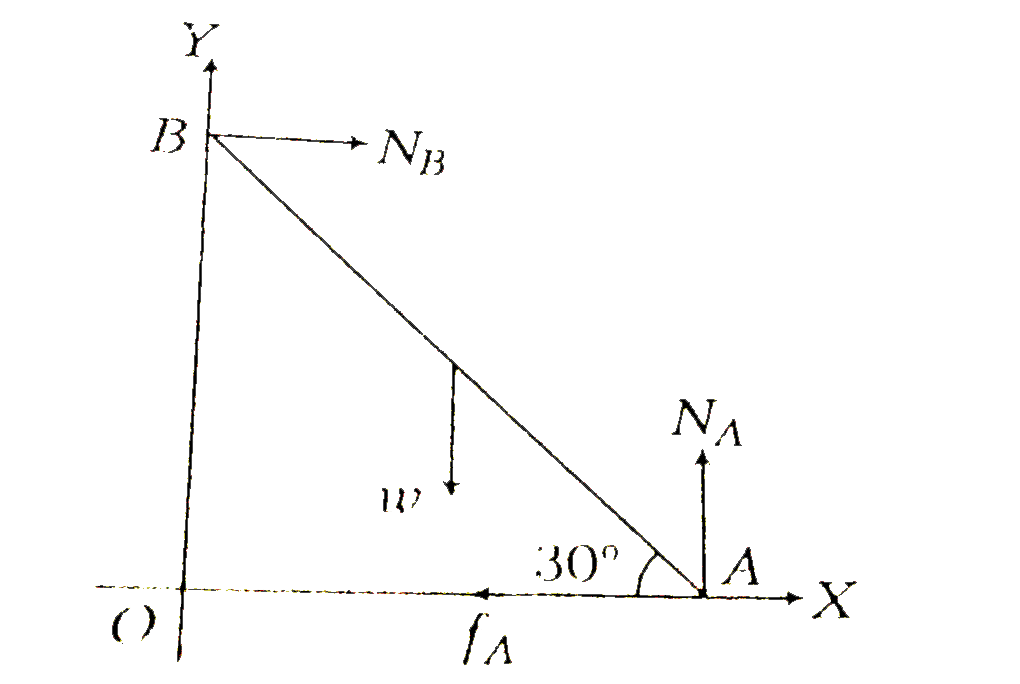
(i) ∑Fx=0
∴NB−fA=0
or NB=fA……….(i)
(ii)∑Fy=0
∴NA−w=0
or NA=w........(ii)
(iii) ∑τ0=0
∴NA(2lcos30∘)−NB(2lsin30∘)−w(lcos30∘)=0
or √3NA−NB−√32w=0........(iii)
Solving these three equations, we get
(a)fA=√32w (b) NA)=w
(c ) NB=√32w
Topper's Solved these Questions
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Check point 5.1
Explore 20 Videos
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Check point 5.2
Explore 15 Videos
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Subjective Question
Explore 27 Videos
- KINEMATICS 1Book:DC PANDEYChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEYChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
Similar Questions
A rod AB rests with the end A on rough horizontal ground and the end B against a smooth vertical wall. The rod is uniform and of weight w. If the rod is in equilibrium in the position shown in figure.Find
(a)frictional shown at A
(b) normal reaction at A
(c) normal reaction at B.

View SolutionA uniform ladder of mass 10 kg leans against a smooth vertical wall making an angle of 530 with it. The other end rests on a rough horizontal floor. Find the normal force and the frictional force that the floor exerts on the ladder
View Solution
Knowledge Check
A uniform rod AB hinged about a fixed point P is initially vertical. A rod is released from vertical position. When rod is in horizontal position:
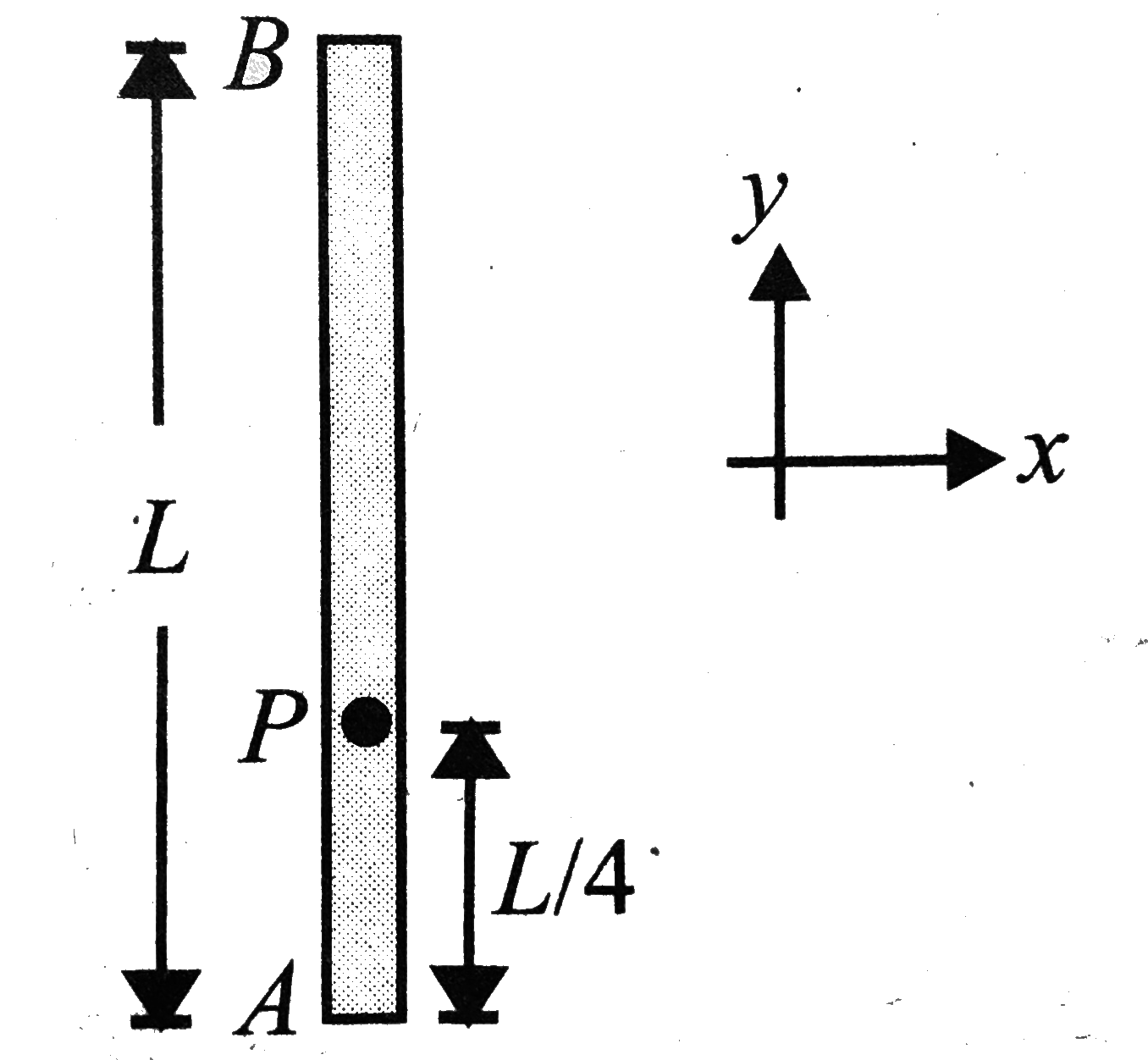
The acceleration of end B of the rod isA−6g7ˆi−12g7ˆjB−5g7ˆi−6g7ˆjC−18g7ˆi−5g7ˆjD−18g7ˆi−9g7ˆjA uniform beam AB of weight W is standing with the end B on a horizontal floor and end A leaning against a vertical wall. The beam stands in a vertical plane perpendicular to the wall inclined at 45∘ to the vertical, and is in the position of limiting equilibrium. If the two points of contact are equally rough, then the coefficient of friction at each of them is
A√2−1B1/√2C1/√3DNoneA uniform ladder rests in limiting equilibrium with its lower end on a rough horizontal plane with coefficient of friction μ and its upper end against a smooth vertical wall. If θ is the inclination of the ladder with the wall, then θ is equal to
Atan−1μBcot−1μCcot−1(2μ)Dtan−1(2μ)
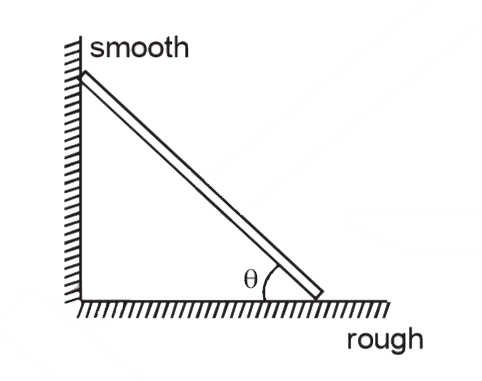
A stationary uniform rod of mass 'm', length 'l' leans against a smooth vertical wall making an angle θ with horizontal floor. Find the normal force & frictional force that is exerted by the floor on the rod ?
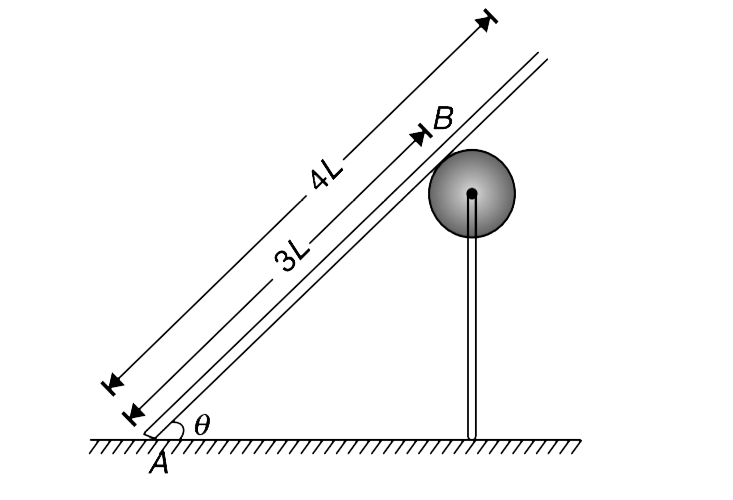
View SolutionA uniform rod has mass M and length 4L. It rests in equilibrium with one end on a rough horizontal surface at A. At point B, at a distance 3L from A, it is supported by a fixed smooth roller. The rod just remains in equilibrium when θ=30∘
(a) Find the normal force applied by the horizontal surface on the rod at point A.
(b) Find the coefficient of friction between the rod and the surface.
View SolutionA rod AB of mass M and length L is shown in figure. End A of rod is hinged and end B is lying on the ground. Find the

Normal reaction by ground on the rod
View SolutionA uniform ladder rests in limiting equilibrium with its lower end on a rough horizontal plane with coefficient of friction μ and its upper end against a smooth vertical wall. If θ is the inclination of the ladder with the wall, then θ is equal to
View SolutionA light rod carries three equal masses A, B and C as shown in figure. Find the velocity of B in vertical position of rod, if it is released from horizontal position. As shown in figure.

View Solution