A rod CD of length b carrying a current l, is placed in a magnetic field due to a thin log wire AB carrying currrent I as shown in fig. Then find the net force experienced by the wire
To find the net force experienced by the rod CD carrying a current I2 in the magnetic field created by the long wire AB carrying a current I1, we will follow these steps:
Step 1: Understand the Setup
We have a thin long wire AB carrying a current I1. A rod CD of length b carrying a current I2 is placed parallel to the wire at a distance A from one end of the rod.
Step 2: Magnetic Field due to the Long Wire
The magnetic field B at a distance X from a long straight wire carrying current I1 is given by the formula:
B=μ0I12πX
where μ0 is the permeability of free space.
Step 3: Force on a Small Element of the Rod
Consider a small element dx of the rod CD at a distance X from the wire. The force dF on this small element due to the magnetic field is given by:
dF=I2⋅dB⋅sin(90∘)=I2⋅μ0I12πX⋅dx
Since sin(90∘)=1, we can simplify this to:
dF=μ0I1I22πXdx
Step 4: Integrate to Find Total Force
To find the total force F on the rod, we need to integrate dF from the lower limit A (the distance from the wire to one end of the rod) to the upper limit A+b (the distance to the other end of the rod):
F=∫A+bAdF=∫A+bAμ0I1I22πXdx
Step 5: Solve the Integral
Taking the constant terms out of the integral:
F=μ0I1I22π∫A+bA1Xdx
The integral of 1X is ln(X):
F=μ0I1I22π(ln(X))A+bA
Evaluating the limits:
F=μ0I1I22π(ln(A+b)−ln(A))
Using the property of logarithms:
F=μ0I1I22πln(A+bA)
Final Expression
Thus, the net force experienced by the rod CD due to the magnetic field of the wire AB is:
F=μ0I1I22πln(1+bA)
We have a thin long wire AB carrying a current I1. A rod CD of length b carrying a current I2 is placed parallel to the wire at a distance A from one end of the rod.
The magnetic field B at a distance X from a long straight wire carrying current I1 is given by the formula:
B=μ0I12πX
where μ0 is the permeability of free space.
Consider a small element dx of the rod CD at a distance X from the wire. The force dF on this small element due to the magnetic field is given by:
dF=I2⋅dB⋅sin(90∘)=I2⋅μ0I12πX⋅dx
Since sin(90∘)=1, we can simplify this to:
dF=μ0I1I22πXdx
To find the total force F on the rod, we need to integrate dF from the lower limit A (the distance from the wire to one end of the rod) to the upper limit A+b (the distance to the other end of the rod):
F=∫A+bAdF=∫A+bAμ0I1I22πXdx
Taking the constant terms out of the integral:
F=μ0I1I22π∫A+bA1Xdx
The integral of 1X is ln(X):
F=μ0I1I22π(ln(X))A+bA
Evaluating the limits:
F=μ0I1I22π(ln(A+b)−ln(A))
Using the property of logarithms:
F=μ0I1I22πln(A+bA)
Thus, the net force experienced by the rod CD due to the magnetic field of the wire AB is:
F=μ0I1I22πln(1+bA)
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IA142videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IB71videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question15videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions3videos
NUCLEAR PHYSICS
Similar Questions
A segment AB of wire carrying current I1 is placed perpendicular to a long straight wire carrying current I2 as shown in figure. The magnitude of force experieced by the straight wire AB is
 View Solution
View SolutionA conductor AB of length L carrying a current I', is placed perpendicular to a long straight conductor XY carrying a current I as shown in Fig. The forces on AB has magnitude
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A wire ABCDEF ( with each side of length L) bent as shown in figure and carrying a current I is placed in a uniform magnetic induction B parallel to the positive y−direction. The force experienced by the wire is ……….. In the ………. direction .
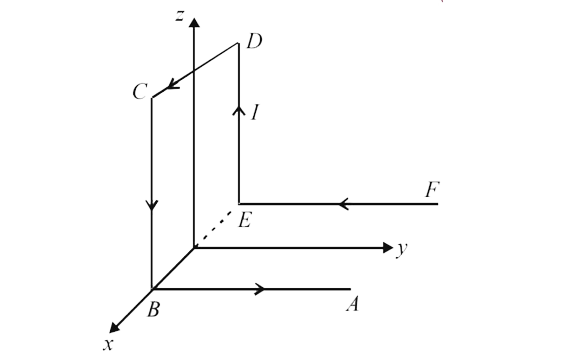 Aa) 2 BILBb) BIL2Cc) BILDd) BIL4
Aa) 2 BILBb) BIL2Cc) BILDd) BIL4
A conductor AB of length L carrying a current I', is placed perpendicular to a long straight conductor XY carrying a current I as shown in Fig. The forces on AB has magnitude
 View Solution
View SolutionA conductor AB of length l carrying current i is placed perpendicular to a long straight conductor carrying a current I as shown. Force on AB will be
 View Solution
View SolutionThree long, straight parallel wires carrying current, are arranged as shown in figure. The force experienced by a 25cm length of wire C is
 View Solution
View SolutionA wire ABCDEF ( with each side of length L) bent as shown in figure and carrying a current I is placed in a uniform magnetic induction B parallel to the positive y−direction. The force experienced by the wire is ……….. In the ………. direction .
 View Solution
View SolutionA thin rod, carrying current i2 is placed near a long straight wire carrying current i1 in the plane of rod as shown in figure. The motion of rod is
View Solutionthe force on current carrying wire placed in uniform magnetic field B as shown in figure is
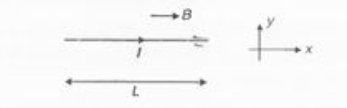 View Solution
View SolutionThe magnetic field in a straight current carrying conductor wire is:
View Solution

